Параллельность прямых в пространстве

ЦЕЛИ УРОКА
1. Рассмотреть взаимное расположение прямых в пространстве
2. Доказать теоремы о параллельности прямых
3. Закрепить понятия на моделях куба, и пирамиды

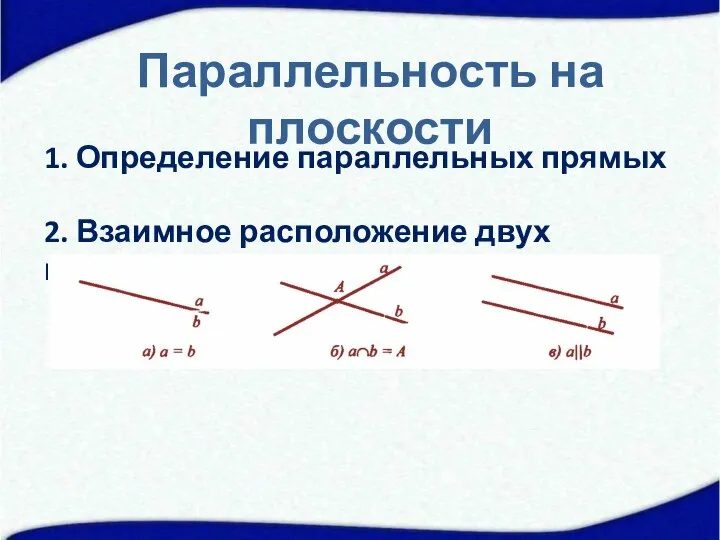
Параллельность на плоскости
1. Определение параллельных прямых
2. Взаимное расположение двух прямых

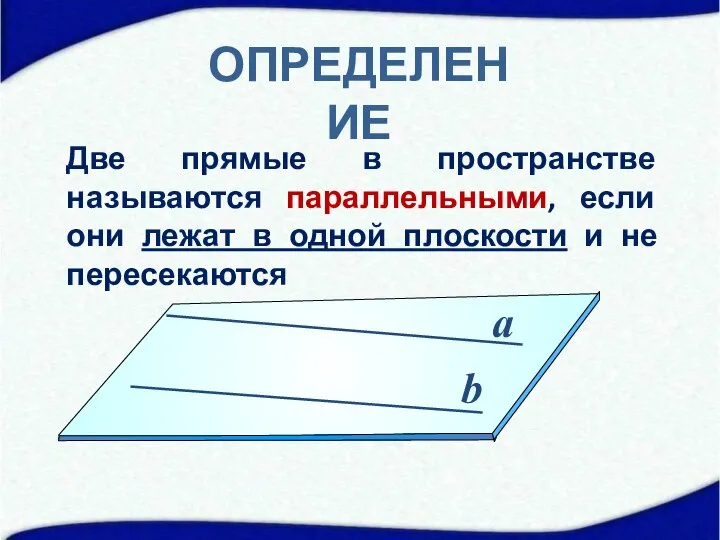
ОПРЕДЕЛЕНИЕ
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются
a
b

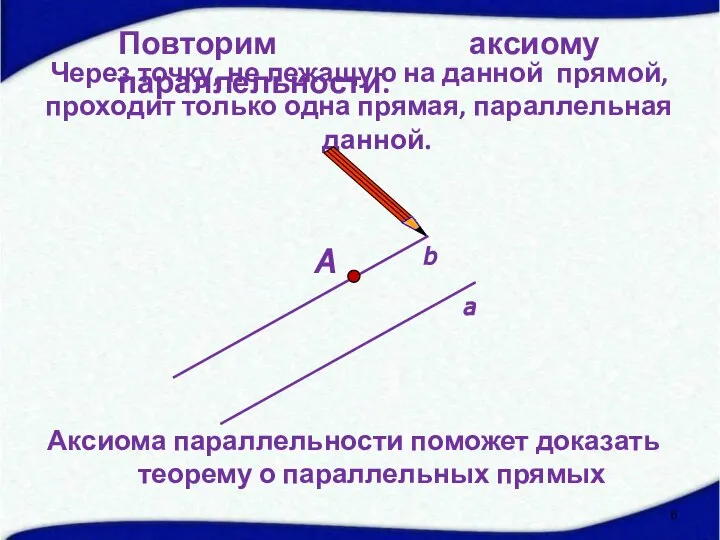
А
Через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная данной.
а
b
Аксиома параллельности поможет доказать теорему о параллельных прямых
Повторим аксиому параллельности.

ТЕОРЕМА
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

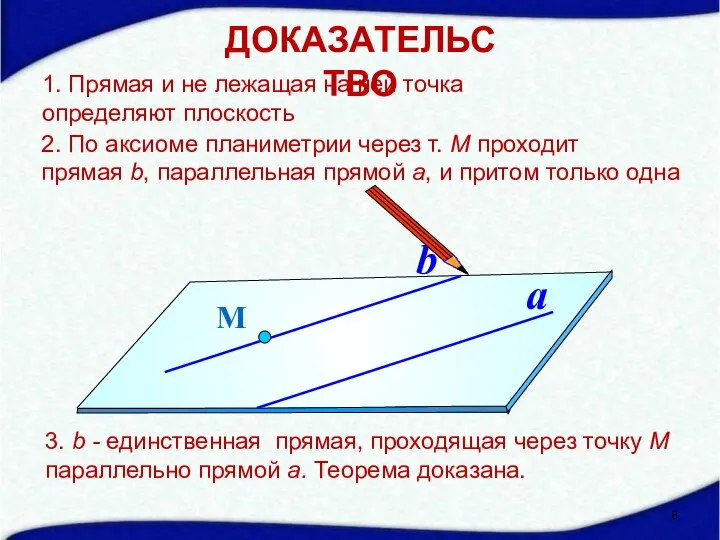
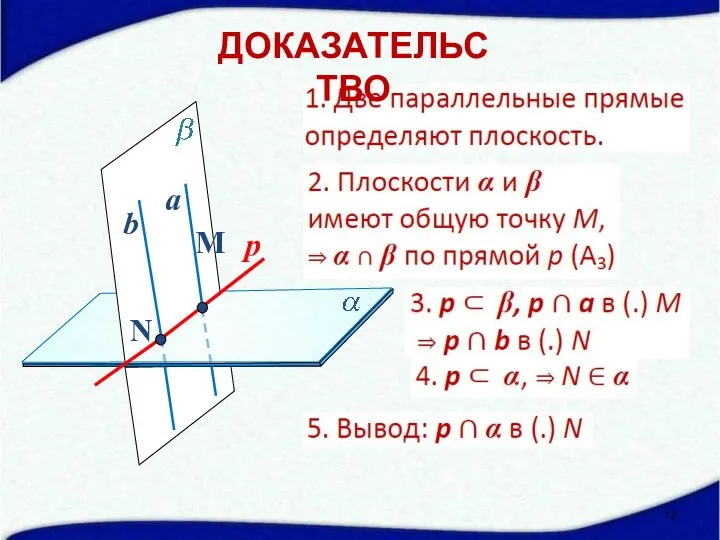
М
a
b
1. Прямая и не лежащая на ней точка
определяют плоскость
ДОКАЗАТЕЛЬСТВО
2. По аксиоме планиметрии через т. М проходит
прямая b, параллельная прямой а, и притом только одна
3. b - единственная прямая, проходящая через точку М
параллельно прямой а. Теорема доказана.

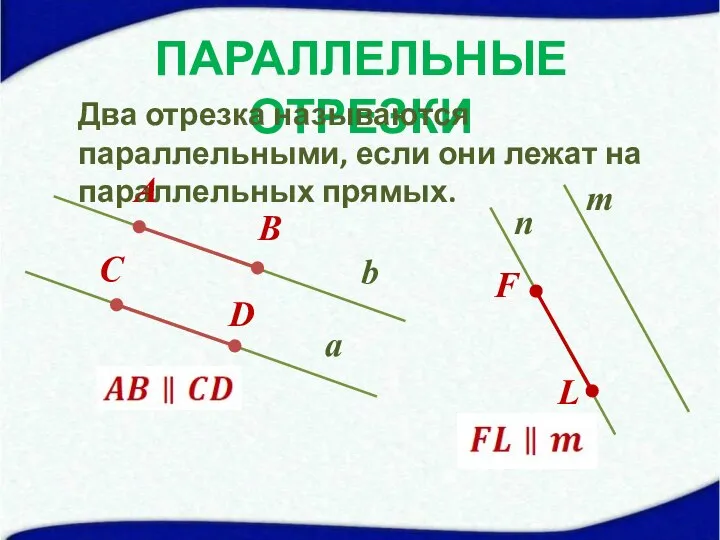
ПАРАЛЛЕЛЬНЫЕ ОТРЕЗКИ
Два отрезка называются параллельными, если они лежат на параллельных прямых.
b
a
А
В
D
С
m
n
L
F

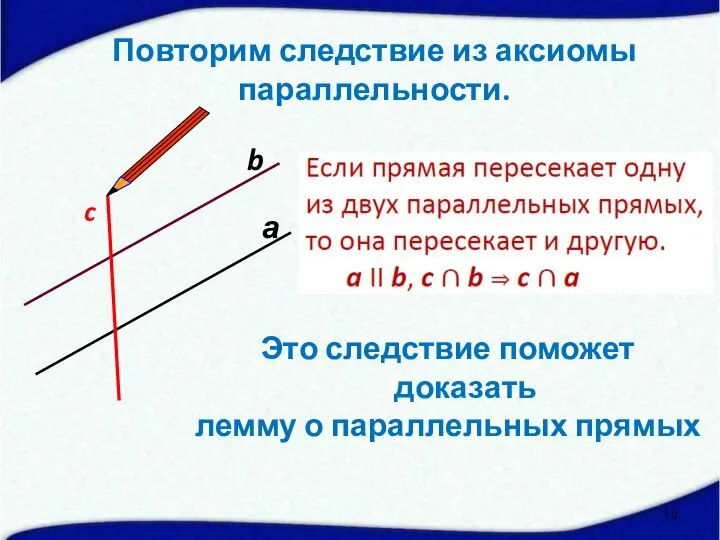
а
c
b
Это следствие поможет доказать
лемму о параллельных прямых
Повторим следствие из аксиомы
параллельности.

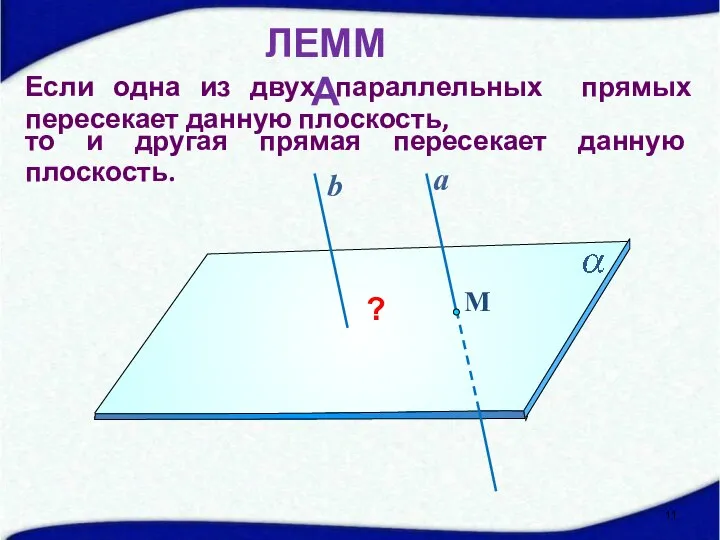
Если одна из двух параллельных прямых пересекает данную плоскость,
М
a
?
b
ЛЕММА
то и другая прямая пересекает данную плоскость.

М
a
ДОКАЗАТЕЛЬСТВО

а
b
с
Повторим следствие из аксиомы
параллельности.
Если две прямые параллельны третьей прямой,
то они параллельны.
Аналогичное утверждение имеет место и для трех
прямых в пространстве.

ТЕОРЕМА
Если две прямые параллельны третьей, то они параллельны
Дано:
Доказать:
a
b
с

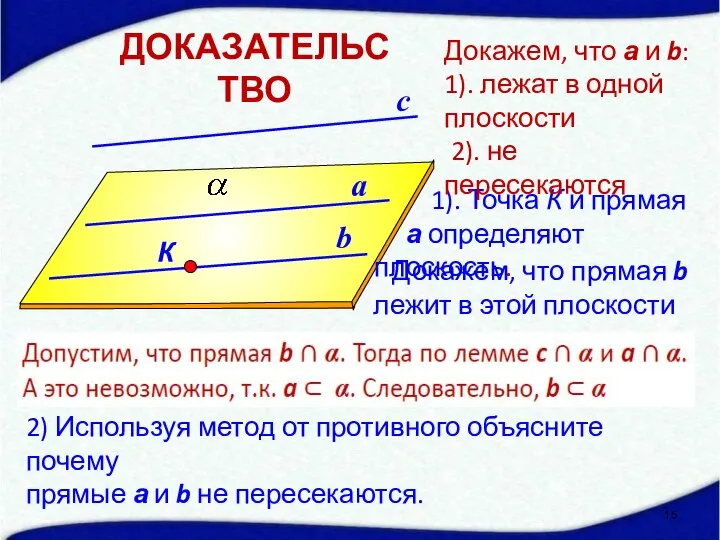
a
b
с
1). Точка К и прямая
а определяют плоскость.
Докажем, что а и b:
1). лежат в одной
плоскости
2). не пересекаются
2) Используя метод от противного объясните почему
прямые а и b не пересекаются.
Докажем, что прямая b
лежит в этой плоскости
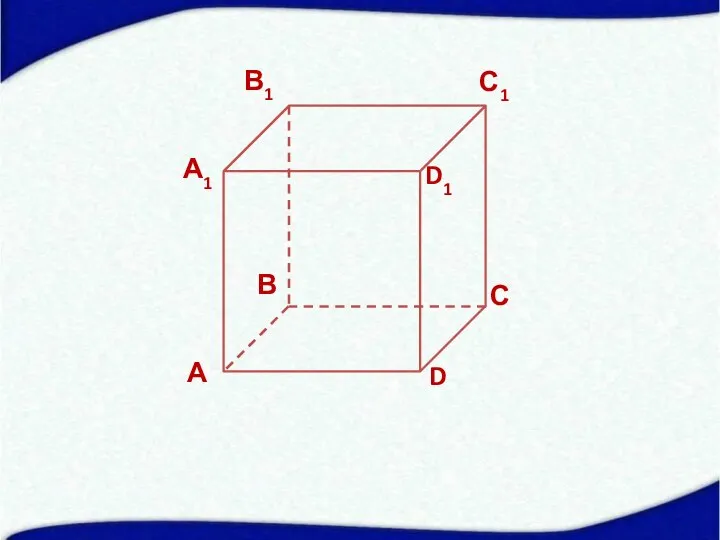
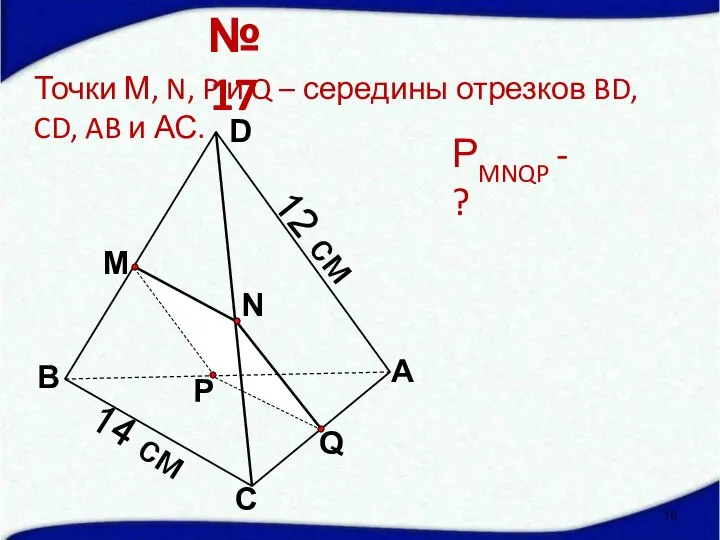
ДОКАЗАТЕЛЬСТВО

Q
А
С
В
D
N
M
P
Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
РMNQP - ?
12 см
14 см
№ 17