- Главная
- Математика
- Решение линейных систем уравнений способом подстановки

Содержание
Слайд 213.05 Классная работа
Решение линейных систем уравнений способом подстановки.
№696(б)
х +5у = 0
13.05 Классная работа
Решение линейных систем уравнений способом подстановки.
№696(б)
х +5у = 0

⬄ (выразим из первого уравнения Х через У.
3х + 7у – 16 = 0 т.к. коэффициент перед Х равен 1 (выразить Х через У, значит Х оставить с лево, а все остальное перенести в право))
х = - 5у ⬄ (подставим -5у во второе уравнение
3х + 7у - 16 = 0 вместо Х)
х= - 5у
3*(- 5у) + 7у – 16 = 0
3х + 7у – 16 = 0 т.к. коэффициент перед Х равен 1 (выразить Х через У, значит Х оставить с лево, а все остальное перенести в право))
х = - 5у ⬄ (подставим -5у во второе уравнение
3х + 7у - 16 = 0 вместо Х)
х= - 5у
3*(- 5у) + 7у – 16 = 0
Слайд 3Решим второе уравнение: - 15у + 7у – 16 = 0
неизвестные влево,
Решим второе уравнение: - 15у + 7у – 16 = 0
неизвестные влево,

известные вправо: - 15у + 7у = 16
(если слагаемое переносим из одной части в другую, то меняем его знак на противоположный)
Считаем сколько с лево, сколько с право: - 8у = 16
Делим обе части на коэффициент перед неизвестным:
у = 16 : (-8)
у = - 2
Подставим значение У в первое уравнения
х = -5* (- 2) ⬄ х = 10
у = - 2 у = - 2
Проверка: 10 + 5*(- 2)= 0 ⬄ 10 – 10 =0 ⬄ 0=0
3*10 + 7*(- 2) – 16 =0 30 – 14 – 16 =0 0=0
Ответ: (10; - 2) (всегда на первом месте пишем значение Х. на втором значение У)
(если слагаемое переносим из одной части в другую, то меняем его знак на противоположный)
Считаем сколько с лево, сколько с право: - 8у = 16
Делим обе части на коэффициент перед неизвестным:
у = 16 : (-8)
у = - 2
Подставим значение У в первое уравнения
х = -5* (- 2) ⬄ х = 10
у = - 2 у = - 2
Проверка: 10 + 5*(- 2)= 0 ⬄ 10 – 10 =0 ⬄ 0=0
3*10 + 7*(- 2) – 16 =0 30 – 14 – 16 =0 0=0
Ответ: (10; - 2) (всегда на первом месте пишем значение Х. на втором значение У)
Слайд 4№696(г)
7х – у = 0 ⬄ у =7х ⬄ у =
№696(г)
7х – у = 0 ⬄ у =7х ⬄ у =

7х
3х – у + 12 = 0 3х – у + 12 = 0 3х – 7х +12 = 0
3х - 7 х +12 = 0
3х - 7 х = - 12
- 4х = - 12
х = - 12: (- 4)
х = 3
у = 7х ⬄ у = 7*3 ⬄ у = 21
х = 3 х= 3 х= 3
Проверка: 7*3 – 21 = 0 ⬄ 0=0
3*3 – 21 + 12 = 0 0=0
Ответ: (3; 21)
3х – у + 12 = 0 3х – у + 12 = 0 3х – 7х +12 = 0
3х - 7 х +12 = 0
3х - 7 х = - 12
- 4х = - 12
х = - 12: (- 4)
х = 3
у = 7х ⬄ у = 7*3 ⬄ у = 21
х = 3 х= 3 х= 3
Проверка: 7*3 – 21 = 0 ⬄ 0=0
3*3 – 21 + 12 = 0 0=0
Ответ: (3; 21)
Слайд 5Домашнее задание
№696(а,в)
Домашнее задание
№696(а,в)

- Предыдущая
Российский паспорт Штыренко Алины АлексеевныСледующая -
Medical Protozoology Перпендикулярные прямые
Перпендикулярные прямые ОГЭ 2020-2021. Задание №7
ОГЭ 2020-2021. Задание №7 Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3
Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3 Отображение множеств. Диаграммы
Отображение множеств. Диаграммы Решение задача на совместную работу. 6 класс
Решение задача на совместную работу. 6 класс Логика. Множества
Логика. Множества Что такое математика?
Что такое математика? Площадь треугольника. Площадь прямоугольного треугольника
Площадь треугольника. Площадь прямоугольного треугольника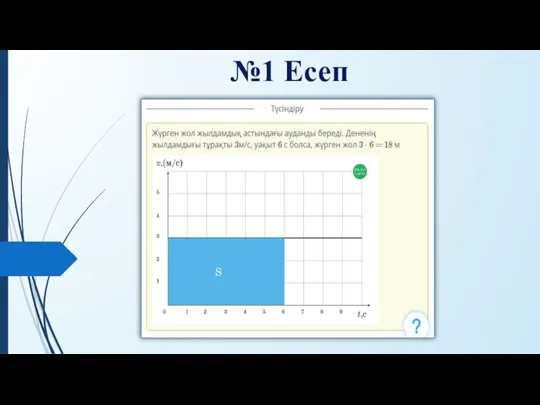 Есептер шығару
Есептер шығару Кривая Лоренца. Решение задач
Кривая Лоренца. Решение задач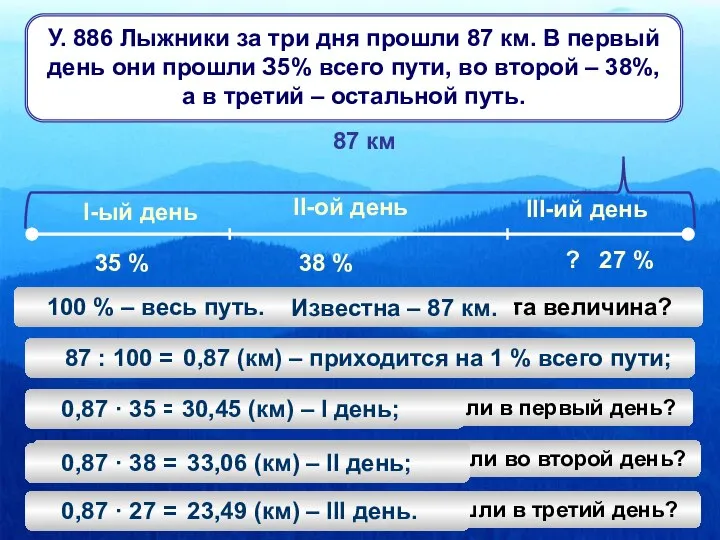 Задачи о лыжниках
Задачи о лыжниках Умножение
Умножение Презентация на тему Вычитание трёхзначных чисел с переходом через разряд
Презентация на тему Вычитание трёхзначных чисел с переходом через разряд  Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  Ломоносов - математик
Ломоносов - математик Перпендикулярные прямые
Перпендикулярные прямые Математические диктанты. 6 класс
Математические диктанты. 6 класс Текстовые задачи. Задание №1
Текстовые задачи. Задание №1 Элементы комбинаторики
Элементы комбинаторики Геометрия. Это полезно знать
Геометрия. Это полезно знать Наглядная геометрия
Наглядная геометрия Математическая игра
Математическая игра Презентация на тему Математика в системе матапредметных знаний учащихся
Презентация на тему Математика в системе матапредметных знаний учащихся  Веселая математика. Головоломки
Веселая математика. Головоломки Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Квадратные неравенства
Квадратные неравенства Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Презентация на тему Цифра 3
Презентация на тему Цифра 3