Содержание
- 2. Задача С2 КИМ 5 июня 2013г. Рассмотрим задачу С2 КИМ 2012 года В прямоугольном параллелепипеде АВСDА₁ВСD₁
- 3. В Стандартная ошибка учащихся F F А В С С₁ D В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны
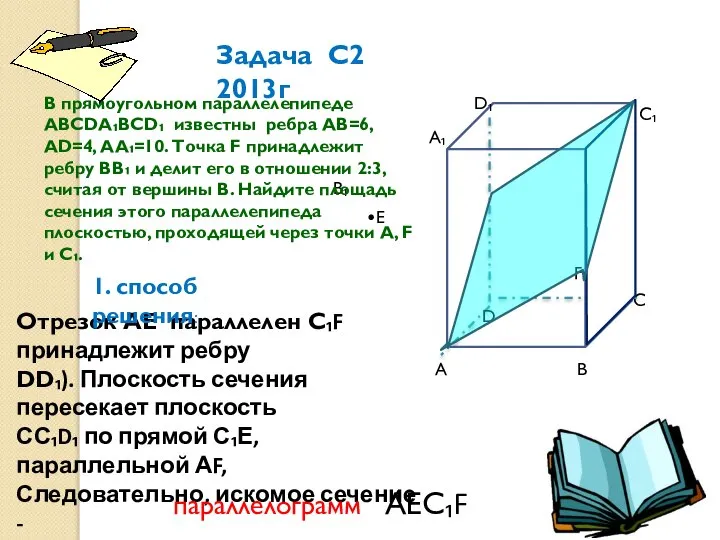
- 4. А А₁ В С С₁ D₁ D В₁ F• • •Е В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны
- 5. Задача С2 2013г А В А₁ С С₁ D₁ D Е F 1. способ решения В₁
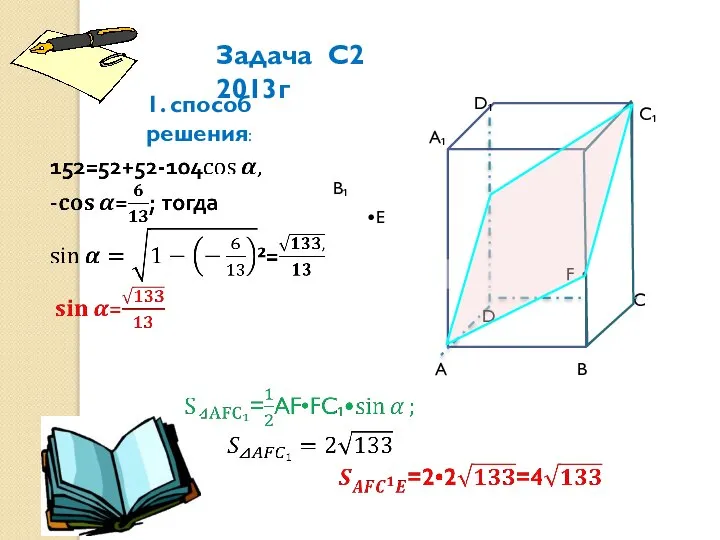
- 6. А А₁ В С С₁ D₁ D В₁ F• •F •Е Задача С2 2013г 1. cпособ
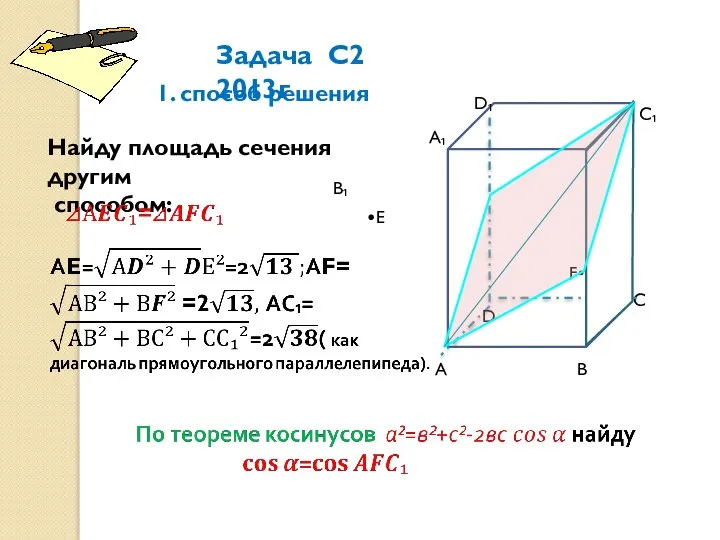
- 7. А А₁ В С С₁ D₁ D В₁ F •F •Е Задача С2 2013г 1. способ
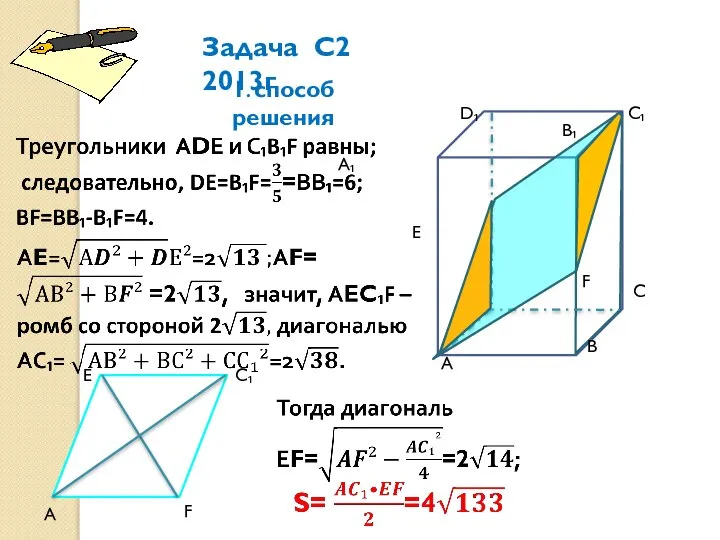
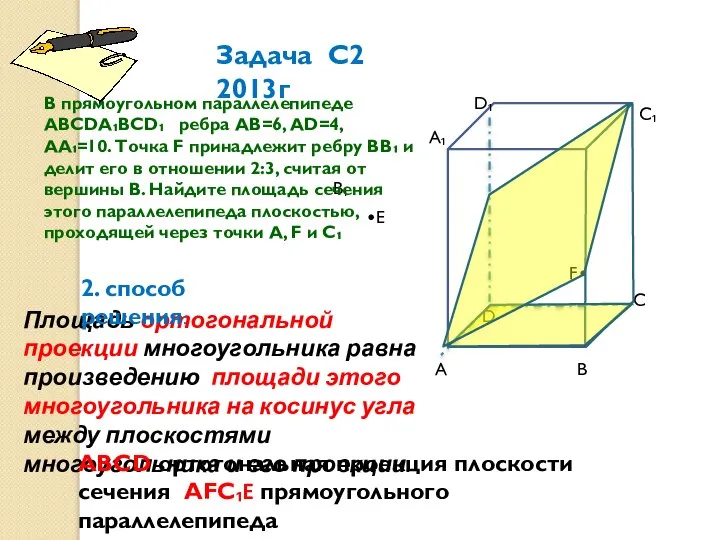
- 8. А А₁ В С С₁ D₁ D В₁ F•F •Е В прямоугольном параллелепипеде АВСDА₁ВСD₁ ребра АВ=6,
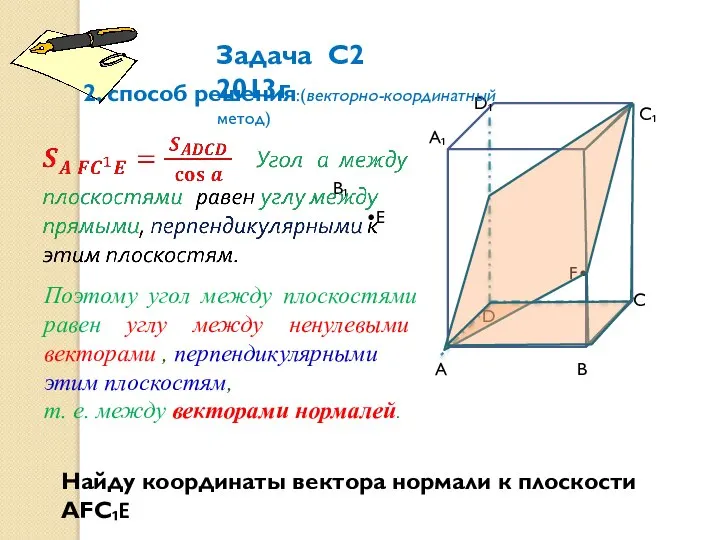
- 9. А А₁ В С С₁ D₁ D В₁ F•F •Е Задача С2 2013г 2. cпособ решения:(векторно-координатный
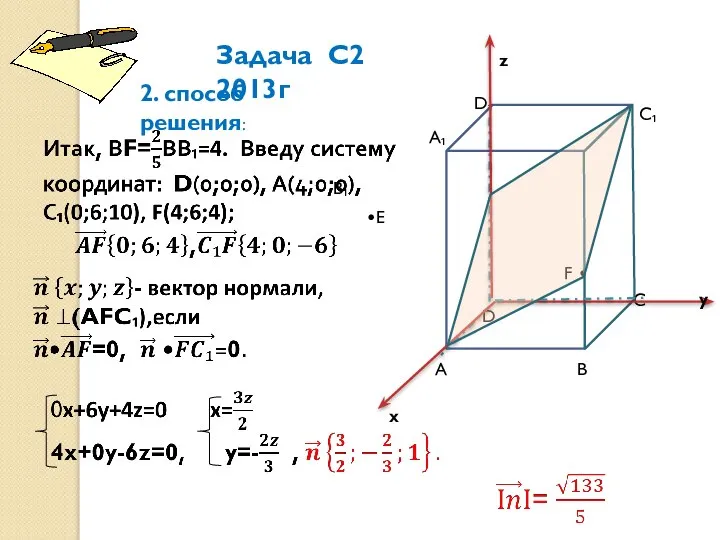
- 10. А А₁ В С С₁ D₁ D В₁ F • •Е Задача С2 2013г 2. способ
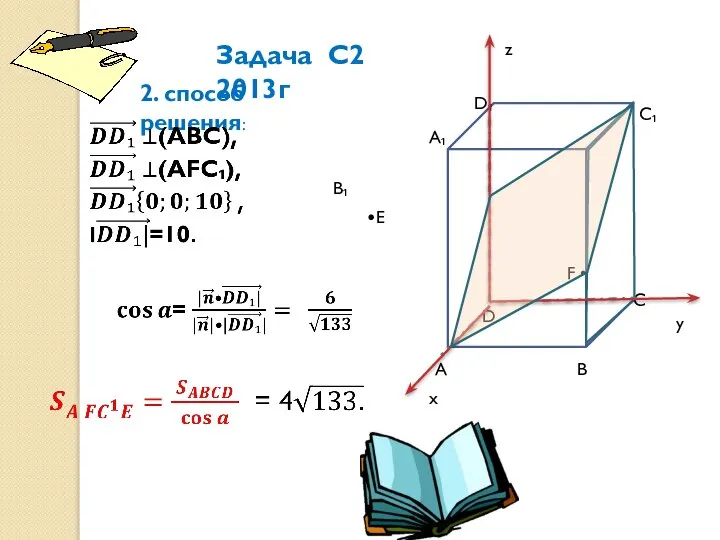
- 11. А А₁ В С С₁ D₁ D В₁ F • •Е Задача С2 2013г 2. способ
- 13. Скачать презентацию


 Сочетательное свойство сложения. Переместительное свойство сложения. Решение задач
Сочетательное свойство сложения. Переместительное свойство сложения. Решение задач Консультация ДУ
Консультация ДУ Сложение и вычитание трёхзначных чисел. Геометрическое задание
Сложение и вычитание трёхзначных чисел. Геометрическое задание Матрицы и действия с матрицами
Матрицы и действия с матрицами Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Презентация на тему Первое знакомство с вероятностью
Презентация на тему Первое знакомство с вероятностью  Прямой счет, обратный счет. Повторение
Прямой счет, обратный счет. Повторение Координаты вектора
Координаты вектора Понятия и свойства функции. Предел функции. Теоремы о пределах. Нахождение пределов функций
Понятия и свойства функции. Предел функции. Теоремы о пределах. Нахождение пределов функций Первый признак равенства треугольников
Первый признак равенства треугольников Сложение и вычитание вида +3, - 3
Сложение и вычитание вида +3, - 3 Физический и геометрический смысл производной
Физический и геометрический смысл производной Математика вокруг нас. Числа в загадках, пословицах и поговорках
Математика вокруг нас. Числа в загадках, пословицах и поговорках Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Математика
Математика Трехмерное моделирование геометрических тел
Трехмерное моделирование геометрических тел Построение сечений тетраэдра
Построение сечений тетраэдра Квадратные неравенства
Квадратные неравенства Естественный отбор. Бинарный урок по биологии и математике (часть 1)
Естественный отбор. Бинарный урок по биологии и математике (часть 1) Векторы. Решение задач
Векторы. Решение задач Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов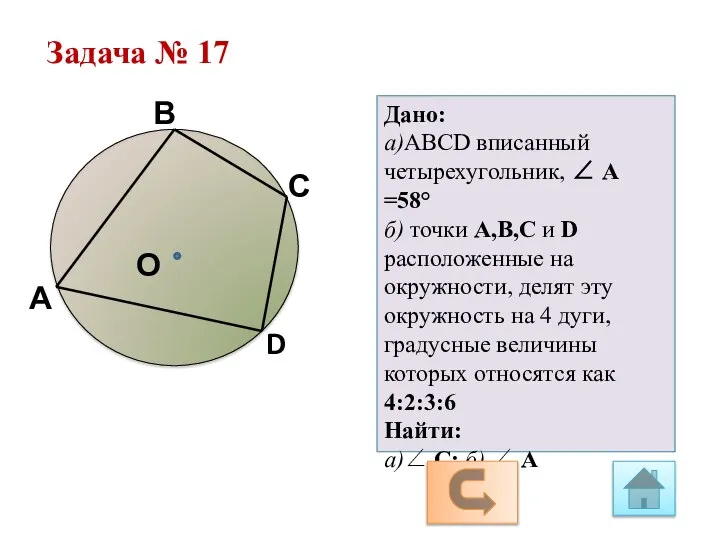 Геометрия 9 класс. Задачи
Геометрия 9 класс. Задачи Площадь прямоугольника. Урок-открытие. 2 класс
Площадь прямоугольника. Урок-открытие. 2 класс Элементы комбинаторики
Элементы комбинаторики Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Задачи с параметрами.Расположение корней квадратного трёхчлена
Задачи с параметрами.Расположение корней квадратного трёхчлена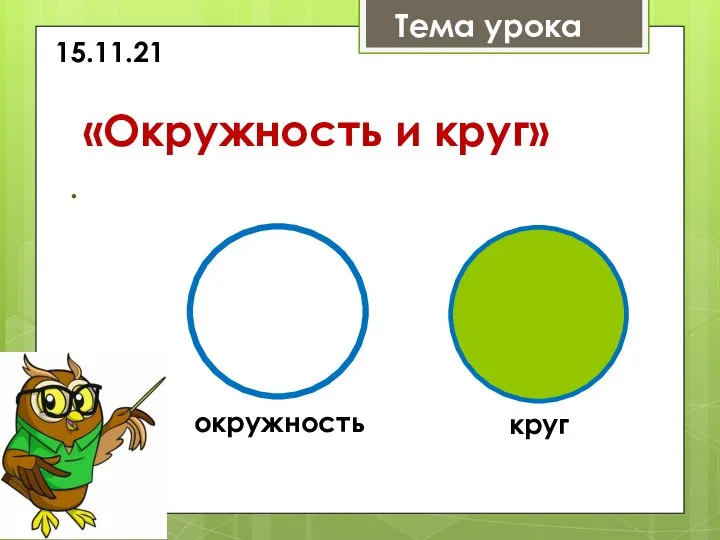 Окружность и круг
Окружность и круг