Треугольник. Подготовка к контрольной работе

( KP=PN=2 CM)
( KL ⊥ MN )
( ⦟ MNH=⦟HNK )

№2 В треугольнике BCD стороны BD и CD равны, DM – медиана, угол BDC равен 38°. Найдите углы BMD и BDM.
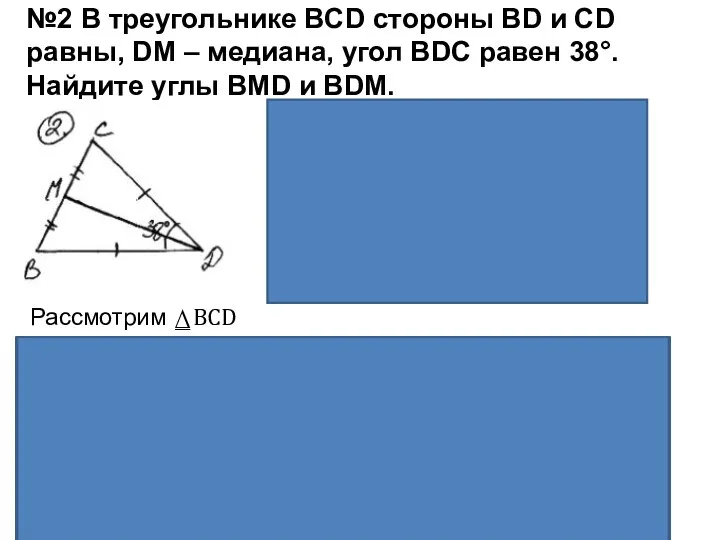
Дано: ⍙BCD
BD=CD
DM- медиана
⦟BDC=38 ̊
Найти:
⦟BDM и ⦟BMD
Решение
Рассмотрим ⍙BCD
BD=CD (по условию) → ⍙BCD – равнобедренный ( по определению)
1) DM- медиана , биссектриса и высота (по свойству равнобедренного треугольника) → ⦟BDM=⦟MDC ( по определению биссектрисы). ⦟BDM= 38:2=19 ̊
2) ⦟BMD=90 ̊ (DM- высота)
Ответ: ⦟BDM=19 ̊, ⦟BMD=90 ̊

№ 3. Луч SC является биссектрисой угла AS В, а отрезки SA и SB равны. Докажите, что Δ SAC = Δ SBC.
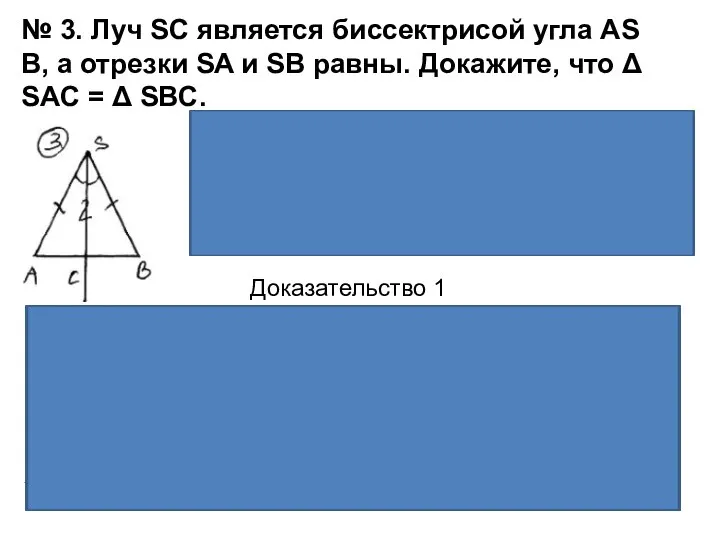
Дано: ⍙ASB – треугольник, SC – биссектриса
SA=SB
Доказать:
⍙SAC=⍙SBC
Доказательство 1
Рассмотрим ⍙ASB
1) SA=SB (по условию) → ASB– равнобедренный ( по определению)
2) ⦟ASC =⦟CSB, тк. SC- биссектриса (по условию)
3) SC – общая
→ ⍙SAC=⍙SBC по I признаку равенства треугольников
Что и требовалось доказать.

№ 5*. Точка D лежит внутри треугольника PRS. Найдите ∠RDS, если RS = PS, DP = DR, ∠RDP = 100°
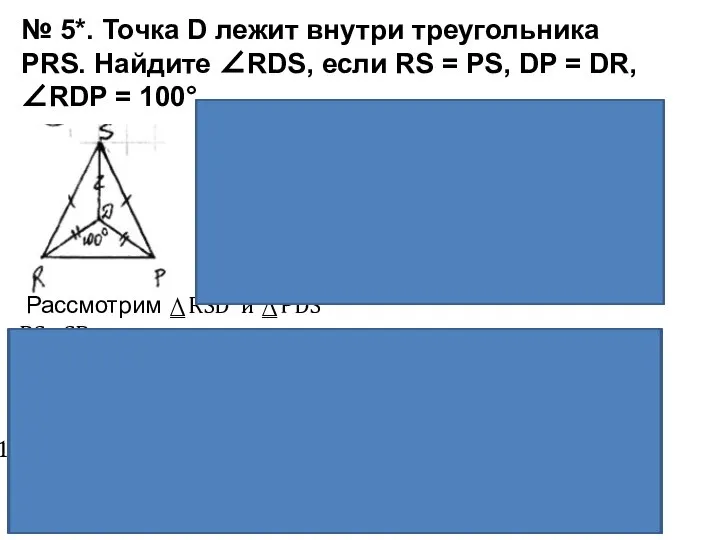
Дано: ⍙PRS – треугольник
RS=SP
DP=DR
⦟RDP= 100 ̊
Найти:
⦟RDS-?
Решение
Рассмотрим ⍙RSD и ⍙PDS
RS=SP
DP=DR
SD – общая →⍙RSD =⍙PDS ( по III признаку равенства треугольников) →⦟RDS =⦟PDS
⦟RDS +⦟RDP+⦟PDS= 360 ̊ → 2 ⦟RDS +⦟RDP= 360 ̊
⦟RDS = (360 ̊- ⦟RDP):2 = (360-100):2=260:2=130 ̊
Ответ: ⦟RDS =130 ̊

№ 4. В окружности с центром О проведены хорды DE и РК, причем ∠DOE = ∠POK. Докажите, что эти хорды равны.