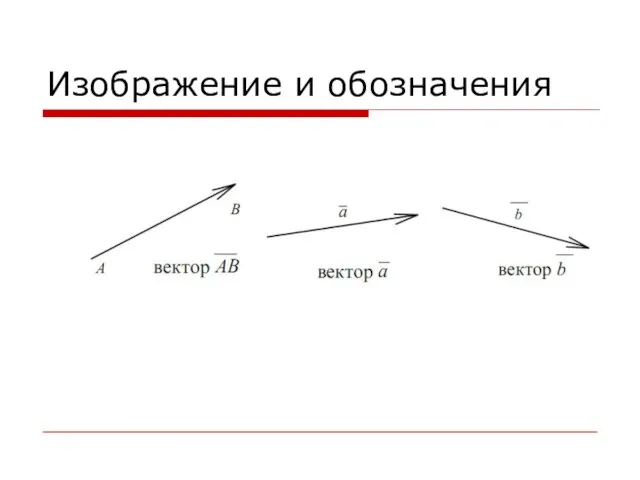
Слайд 2 Векторы
Определение. Вектором назовём направленный отрезок, т.е. отрезок прямой, ограниченный двумя

точками, одна из которых называется начальной, а другая конечной.
Слайд 6Компланарные векторы
Вектор, точка приложения которого может быть выбрана произвольно, называют свободным.

Слайд 7 Линейные операции над векторами
К линейным операциям относятся операции умножения вектора

на
число, сложения и вычитания векторов.
Слайд 13Свойства линейных операций над векторами

Слайд 15 Линейная зависимость векторов. Аффинный базис

Слайд 26Длина вектора, заданного концами – расстояние между точками

Слайд 27 Направляющие косинусы вектора
Направление вектора в пространстве определяется углами α, β

и γ между вектором и положительным направлением соответствующих осей координат ОХ, ОУ, ОZ; cos α, cos β и cos γ называются направляющими косинусами вектора.
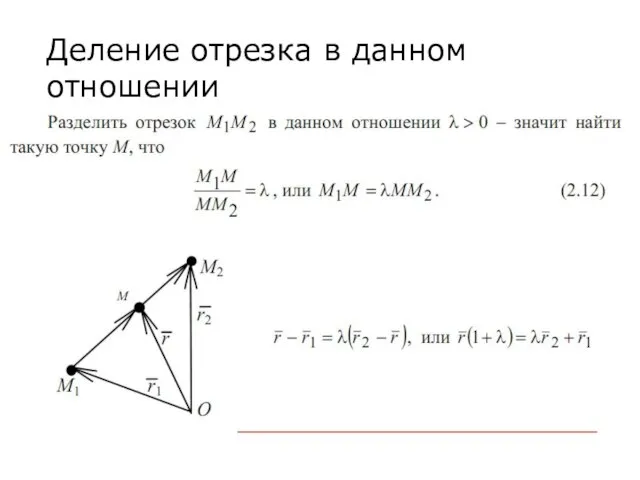
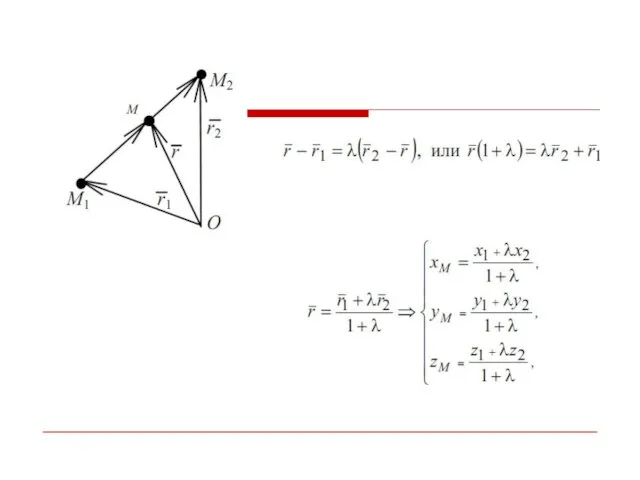
Слайд 29Деление отрезка в данном отношении
Слайд 32Свойства скалярного произведения

Слайд 34 Вычисление проекции вектора на вектор

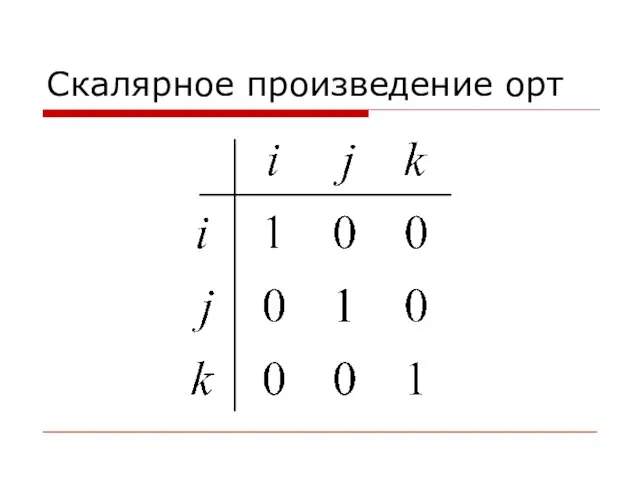
Слайд 35Скалярное произведение в декартовой системе координат

Слайд 37Скалярное произведение векторов равно сумме произведений их одноименных проекций

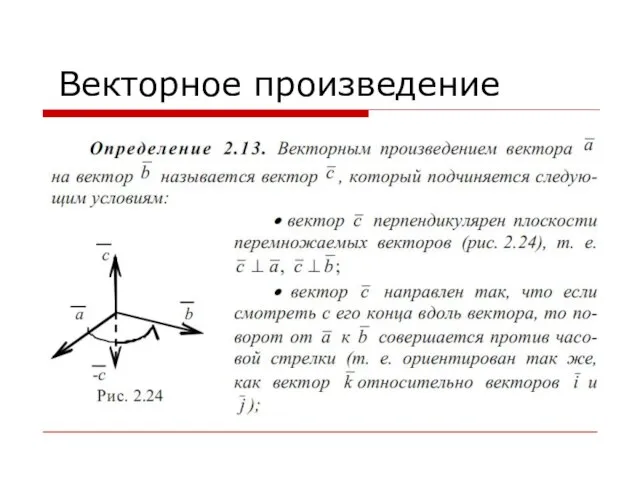
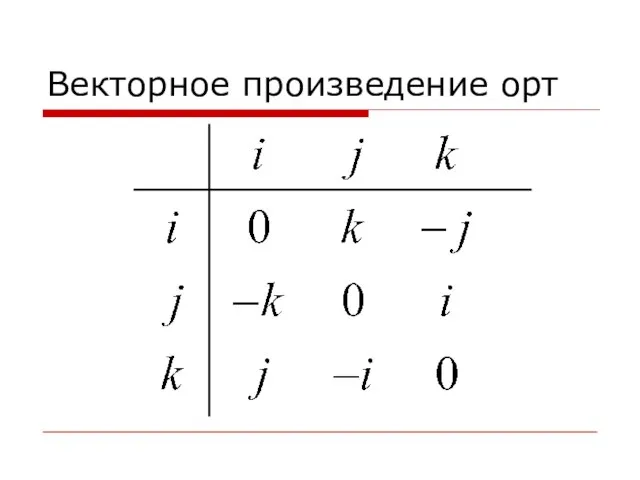
Слайд 41Основные свойства векторного произведения

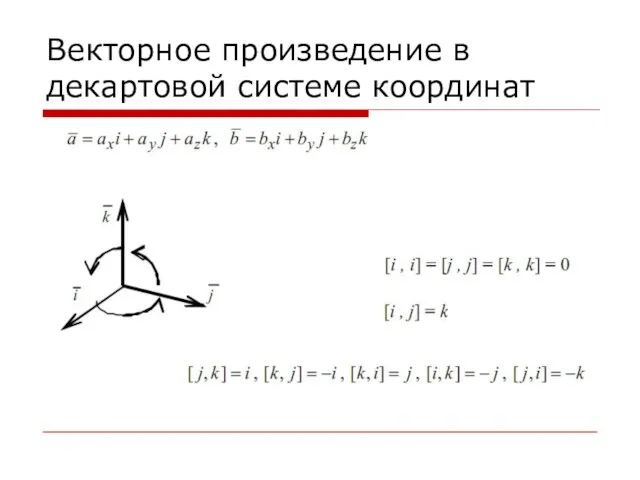
Слайд 43Векторное произведение в декартовой системе координат
Слайд 46С помощью определения векторного произведения можно решать задачу о вычислении площади треугольника,
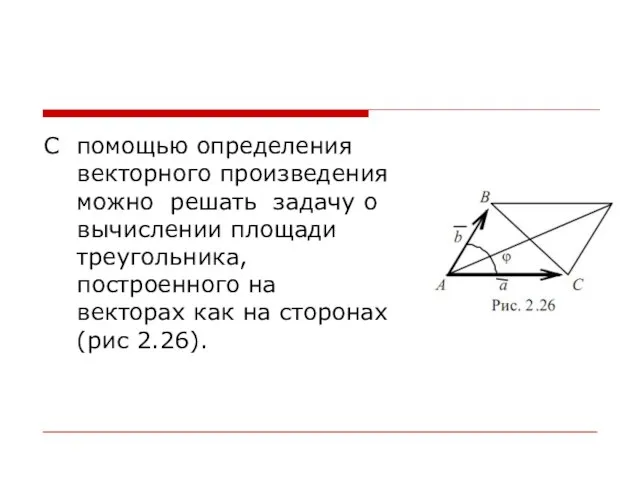
построенного на векторах как на сторонах (рис 2.26).
Слайд 48 Смешанное произведение трёх векторов

Слайд 49Смешанное произведение в декартовой системе координат
Вычислим предварительно векторное произведение

Слайд 51Геометрический смысл смешанного произведения
Построим на векторах как на рёбрах параллелепипед
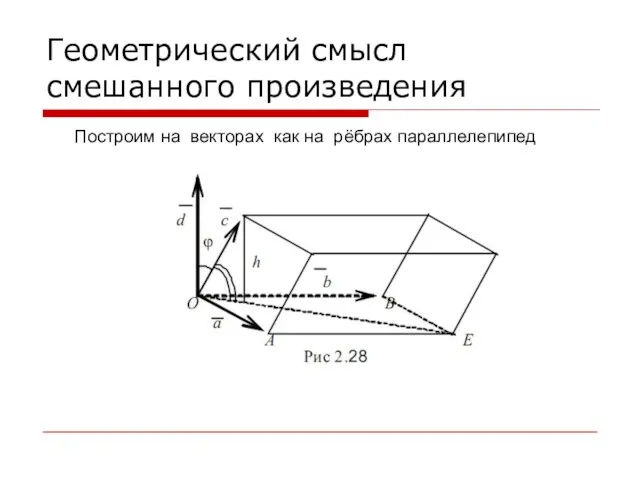
Слайд 53Вывод: модуль смешанного произведения трёх векторов равен объёму параллелепипеда, построенного на этих

векторах как на рёбрах.
Слайд 54Свойства смешанного произведения
Все свойства смешанного произведения доказываются с помощью свойств определителя!







































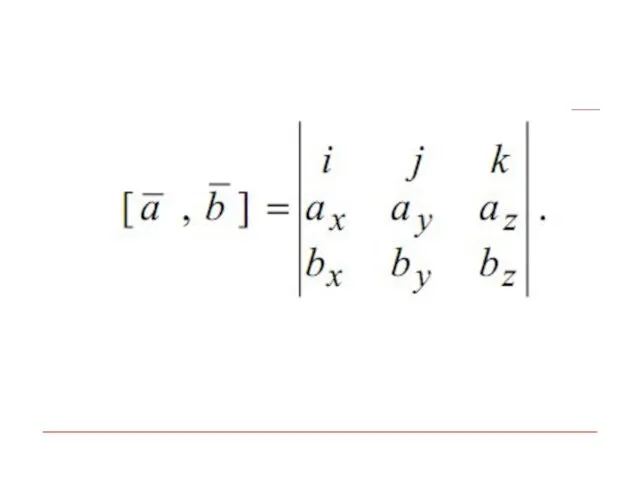









 Доли. 3 класс
Доли. 3 класс Решение задач. Продолжи ряд чисел
Решение задач. Продолжи ряд чисел Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости
Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости Линейные операторы и их матрицы. Ядро и образ линейного оператора. Семинар 6
Линейные операторы и их матрицы. Ядро и образ линейного оператора. Семинар 6 Прямая на плоскости
Прямая на плоскости Числовые ряды, основные определения и свойства
Числовые ряды, основные определения и свойства Методы измерений в квалиметрии
Методы измерений в квалиметрии лекция3 (2)
лекция3 (2) Треугольники
Треугольники Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2
Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей. Лекция 2 Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Таблицы по алгебре
Таблицы по алгебре Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Решение неравенств
Решение неравенств Определённый интеграл. 11 класс
Определённый интеграл. 11 класс Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Симметрия
Симметрия Путешествие по океану МиФ Математики и Фантазии
Путешествие по океану МиФ Математики и Фантазии Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Презентация на тему Конкретный смысл действия умножения (2 класс)
Презентация на тему Конкретный смысл действия умножения (2 класс)  Прибавление и вычитание числа 3. Помоги белочке
Прибавление и вычитание числа 3. Помоги белочке Приключение олобка на тропинке умножения. Тренажер
Приключение олобка на тропинке умножения. Тренажер Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Презентация на тему Деление двузначного числа на однозначное
Презентация на тему Деление двузначного числа на однозначное  повторение 7-9
повторение 7-9 Множества
Множества Построить линейный угол двугранного угла
Построить линейный угол двугранного угла