Взаимное расположение прямых и плоскостей

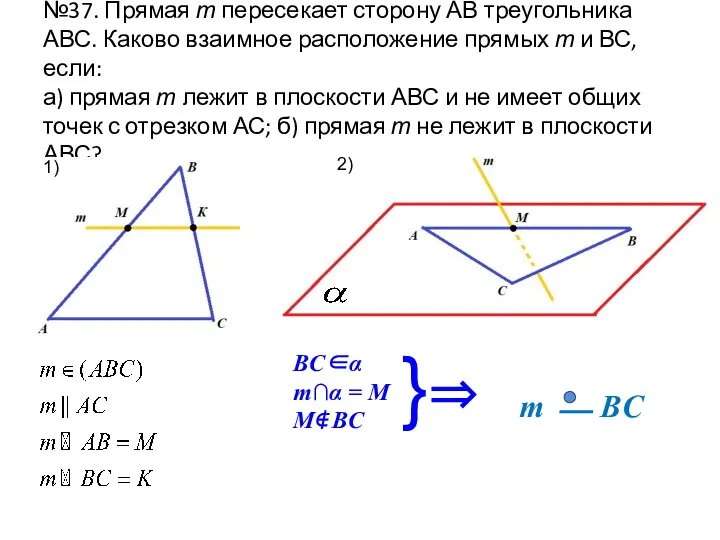
№37. Прямая т пересекает сторону АВ треугольника АВС. Каково взаимное расположение прямых т и ВС, если:
а) прямая т лежит в плоскости АВС и не имеет общих точек с отрезком АС; б) прямая т не лежит в плоскости АВС?
1)
2)
BC∈α
m∩α = M
M∉ BC
}⇒
m ⎯ BC

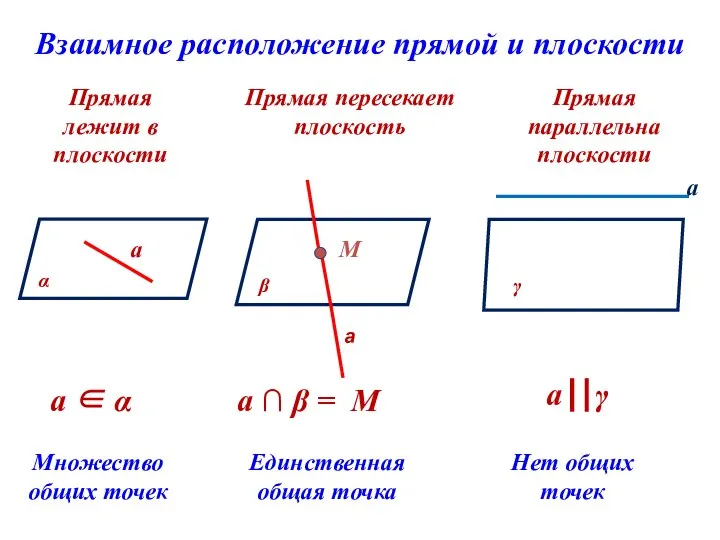
Взаимное расположение прямой и плоскости
Прямая лежит в плоскости
Прямая пересекает плоскость
Прямая параллельна плоскости
Множество общих точек
Единственная общая точка
Нет общих
точек
α
а
β
а
М
γ
а
а ∈ α
а ∩ β = М
а⎟ ⎢γ

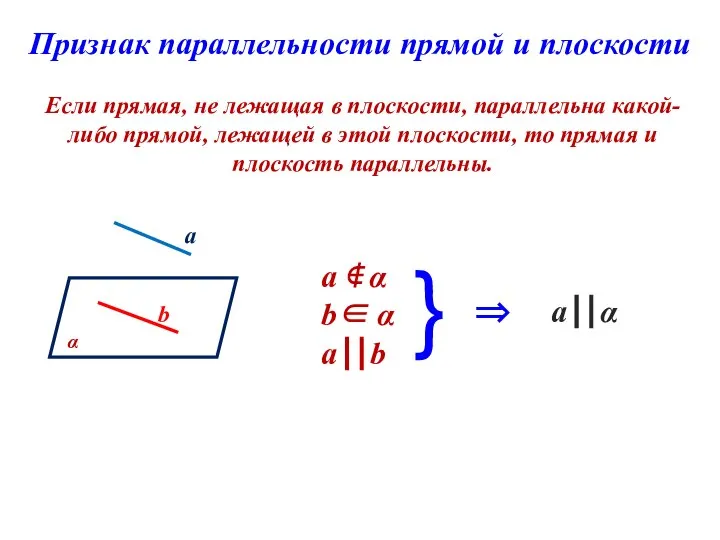
Признак параллельности прямой и плоскости
Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то прямая и плоскость параллельны.
α
а
b
a ∉ α
b∈ α
a⎟ ⎢b
}
⇒
a⎟ ⎢α

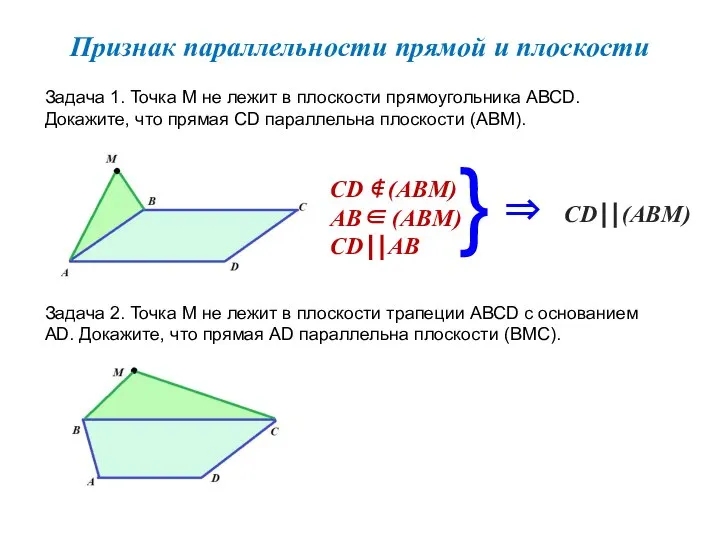
Признак параллельности прямой и плоскости
Задача 1. Точка М не лежит в плоскости прямоугольника АВСD. Докажите, что прямая СD параллельна плоскости (АВМ).
Задача 2. Точка М не лежит в плоскости трапеции АВСD с основанием АD. Докажите, что прямая AD параллельна плоскости (ВМC).
CD ∉ (ABM)
AB∈ (ABM)
CD⎟ ⎢AB
}
⇒
CD⎟ ⎢(ABM)

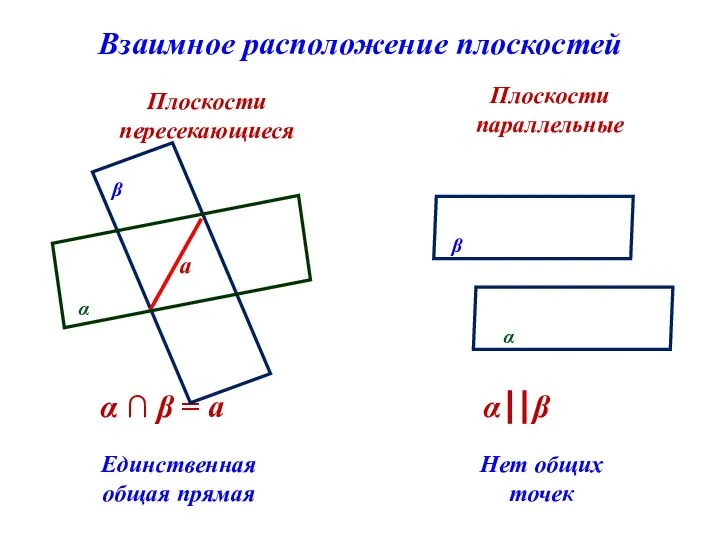
Взаимное расположение плоскостей
Плоскости пересекающиеся
Плоскости параллельные
Единственная общая прямая
Нет общих
точек
α ∩ β = а
α⎟ ⎢β
α
а
β
β
α

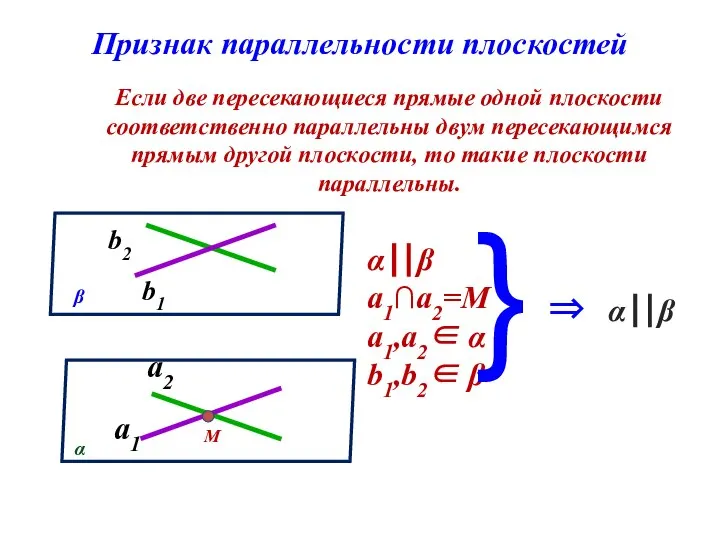
Признак параллельности плоскостей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
β
α
a1
a2
b1
b2
α⎟ ⎢β
a1∩a2=M
a1,a2∈ α
b1,b2∈ β
M
α⎟ ⎢β
}
⇒

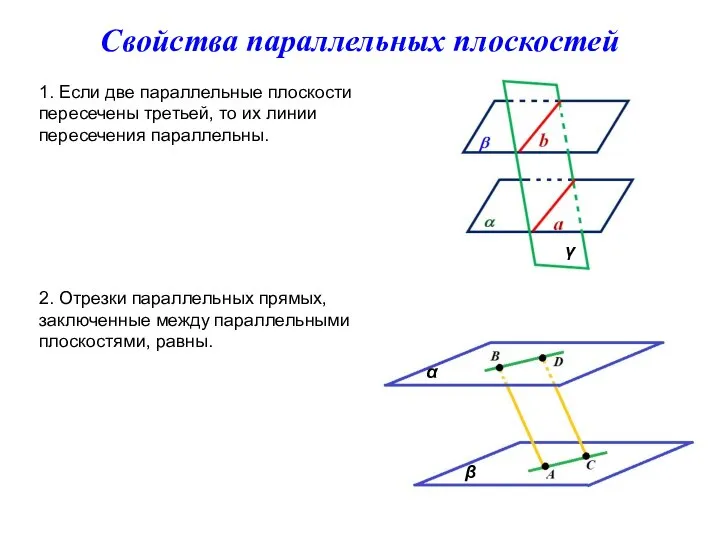
Свойства параллельных плоскостей
γ
1. Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны.
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
α
β