Слайд 2Когда считаем палочками – в Википедии это называется
(ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!)
«Единичная

непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть
УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
Слайд 3В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так

называется, потому что у нас есть десять цифр.
К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах
2; 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Слайд 4Десятичная система счисления
Как мы складываем в 10-СС?
Например, столбиком:
12
+ 99

Слайд 5Сначала складываем единицы:
2+9 = 11, т.е. при сложении двух единичных чисел

появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это
9+9 = 18.
Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем
2+9 +10+90,
т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
Слайд 612 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим
![12 + 99 = [разобьем на разряды] = (2+9) + (10+90) =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/988244/slide-5.jpg)
первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
= 1 + 10 + 100
Слайд 7Получится 111,
но давайте остановимся и посмотрим на эту полученную форму записи:
1

+ 10 + 100
Слайд 8Интересно, что любое число можно представить как сумму отдельно единиц, отдельно десятков,

сотен и т.д., например:
564 = 500 + 60 + 4,
7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули.
Запомните этот момент – это важно.
Слайд 9При этом вместо того, чтобы писать 1000, мы можем написать 103 (т.е.

десять в третьей степени,
,
что можно расшифровать как 10×10×10).
Слайд 10В частности:
7000 = 7×1000 = 7 × 103
А всё число 7031 можно

расписать так:
7031 = 7×103 + 0×102 + 3×101 + 1×100
Слайд 11Напомню, что любое число в нулевой степени даёт единицу, и 100 =

1, а любое число в первой степени даёт само себя 101 = 10.
Еще напомню, что любое число умноженное на 0 даёт 0, т.е.
0×102 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Слайд 12Не путайте числа и цифры!
Путать цифры и числа – это как

путать буквы и звуки.
Цифра – это просто символ
для записи чисел.
А число – это абстрактная величина, обычно означающее количество чего-нибудь.
Слайд 13Двоичная система счисления
Теперь, поговорим о 2-СС.
Её особенность в том, что в ней

есть всего 2 символа для записи чисел:
0 и 1.
Что интересно, при этом любое число, которое можно записать
в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Слайд 14Двоичная система тоже позиционная и отличается от десятичной тем, что в ней

вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
5 4 3 2 1 0
101101= 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Слайд 15Теперь давайте поскладываем в двоичной системе.

Слайд 16Начнём с простого:
0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего

удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
Разве десять???
А вот никакие не ДЕСЯТЬ!
Это число ДВА. Просто в двоичной записи.
Слайд 17Дальше: 10 + 1 = 11
Нет!!! Это не десять плюс один!
Это

два плюс один!
В 10-СС это выглядит так:
2 + 1 = 3, а в 1-СС так:
|| + | = |||.
Усложняем программу:
11 + 1 = ?
Слайд 18сложновато? Давайте упростим!
По той же схеме, что и 12 + 99.

Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! «1+1» складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
= 100
Слайд 19Это не СТО!!! Если то же самое записать в 10-СС, то получим:

3 + 1 = 4.
Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.




![12 + 99 = [разобьем на разряды] = (2+9) + (10+90) =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/988244/slide-5.jpg)













 Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів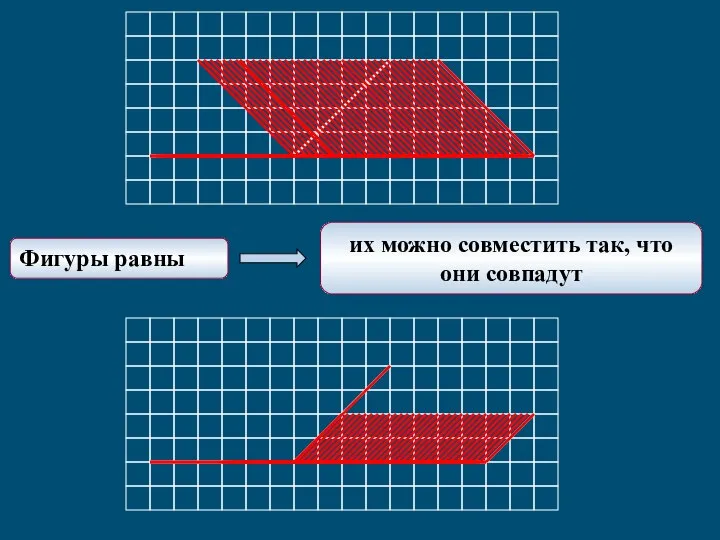 Равенство углов наложением
Равенство углов наложением Описательная статистика
Описательная статистика Применение производной к исследованию функции и построению графика
Применение производной к исследованию функции и построению графика mnozhestva_i_operatsii_nad_nimi (2)
mnozhestva_i_operatsii_nad_nimi (2) Решение заданий
Решение заданий Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение графика производной методом касательных
Построение графика производной методом касательных Ключевые задачи по теме пирамида
Ключевые задачи по теме пирамида Понятие множество и способы задания. 2 класс
Понятие множество и способы задания. 2 класс Древнеяпонские числительные. Задачи
Древнеяпонские числительные. Задачи Правильные многогранники
Правильные многогранники Можно ли без шаблона разметить круг?
Можно ли без шаблона разметить круг? Число потоков в графе
Число потоков в графе Логарифмы
Логарифмы Как не забыть математику за лето советы методиста
Как не забыть математику за лето советы методиста Отношение. Пропорция
Отношение. Пропорция Вероятность и статистика
Вероятность и статистика formuly_privedenia
formuly_privedenia Квадратные уравнения
Квадратные уравнения Сочетания. 9 класс
Сочетания. 9 класс Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Функциональная грамотность школьников на уроках математики
Функциональная грамотность школьников на уроках математики Движение
Движение Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г
Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников