Содержание
- 2. ПЛАН ЛЕКЦИИ 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦ 3. ОПЕРАЦИИ
- 3. ПОНЯТИЕ И ВИДЫ МАТРИЦ
- 4. ОПРЕДЕЛЕНИЯ МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ. ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.
- 5. ВИДЫ МАТРИЦ
- 6. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ
- 7. ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ СТРОКИ НУМЕРУЮТСЯ СВЕРХУ ВНИЗ, НАЧИНАЯ С № 1. СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
- 8. СТРОКА И СТОЛБЕЦ
- 9. РАЗМЕР МАТРИЦЫ МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ РАЗМЕРА m НА n.
- 10. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
- 11. ЭЛЕМЕНТ МАТРИЦЫ
- 12. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
- 13. ТРЕУГОЛЬНЫЕ МАТРИЦЫ
- 14. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 15. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
- 16. МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
- 17. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
- 18. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
- 19. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
- 20. ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА,
- 21. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
- 22. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
- 23. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
- 24. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
- 25. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
- 26. § 1. Матрицы и действия над ними 1. Определение и некоторые виды матриц ОПРЕДЕЛЕНИЕ. Матрицей размера
- 27. Две матрицы A и B считаются равными, если они одинакового размера, и элементы, стоящие в A
- 28. Некоторые частные случаи матриц
- 29. Элементы a11, a22, …, akk (где k = min{m,n}) будем называть элементами главной диагонали матрицы. Квадратная
- 30. 5) Пусть A = (aij) – квадратная матрица порядка n. Элементы a1n, a2,n-1, a3,n-2, …, an1
- 31. 6) Прямоугольную матрицу размера m × n будем называть трапециевидной, если все ее элементы ниже главной
- 32. 2. Линейные операции над матрицами 1) Умножение матрицы на число; 2) Сложение матриц. ОПРЕДЕЛЕНИЕ. Произведением матрицы
- 33. ОПРЕДЕЛЕНИЕ. Суммой двух матриц A=(aij) и B=(bij) одинакового размера, называется такая матрица C=(cij), элементы которой равны
- 34. Свойства линейных операции над матрицами
- 35. 3. Нелинейные операции над матрицами 1) Умножение двух матриц; 2) Транспонирование матрицы. ОПРЕДЕЛЕНИЕ. Пусть A=(a1i) и
- 36. ОПРЕДЕЛЕНИЕ. Пусть A=(aij) – матрица размера m × n, B=(bij) – матрица размера n × k
- 37. Свойства операции умножения матриц
- 38. ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m × n. Матрица размера n × m, полученная из
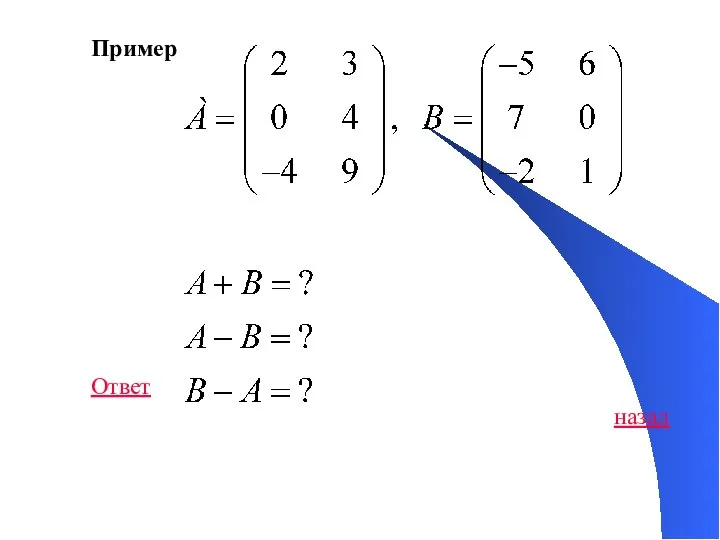
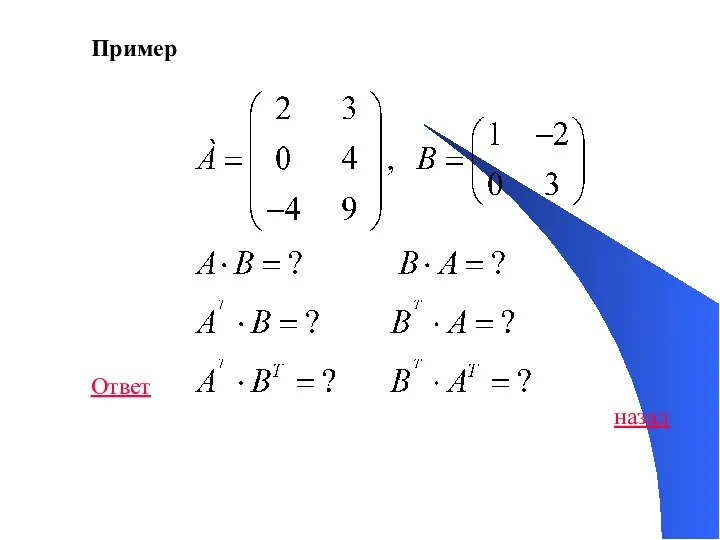
- 39. Пример Ответ назад
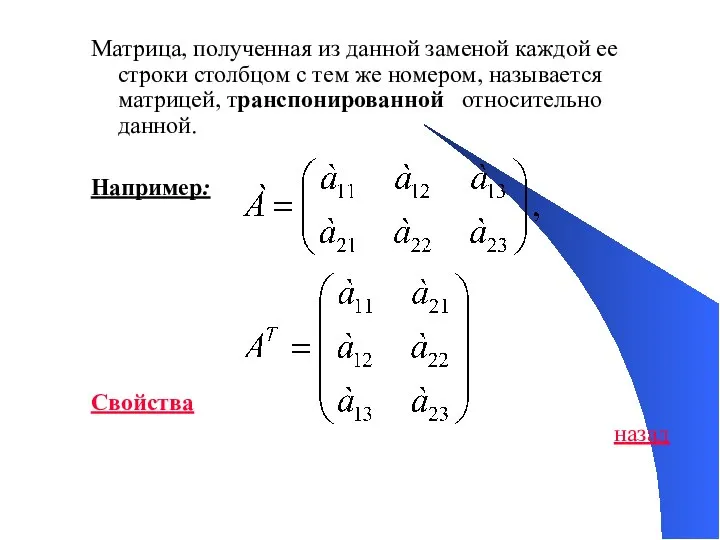
- 40. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной
- 41. В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными. Пример 1. Найти все
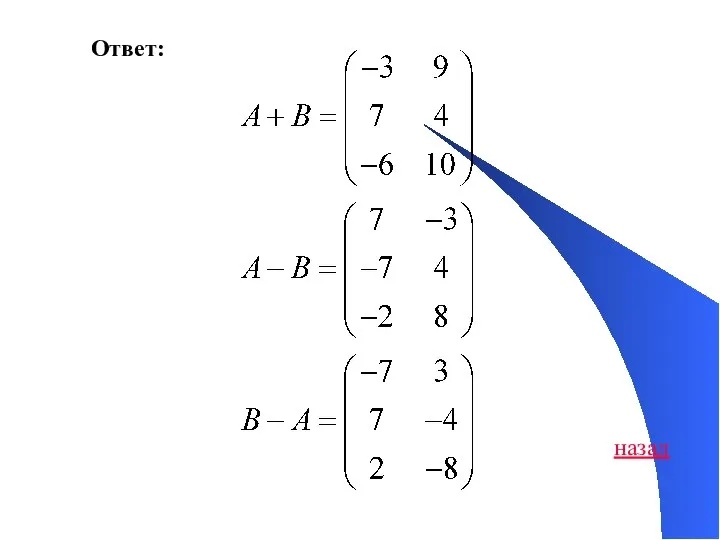
- 42. Ответ: назад
- 43. Пример Ответ назад
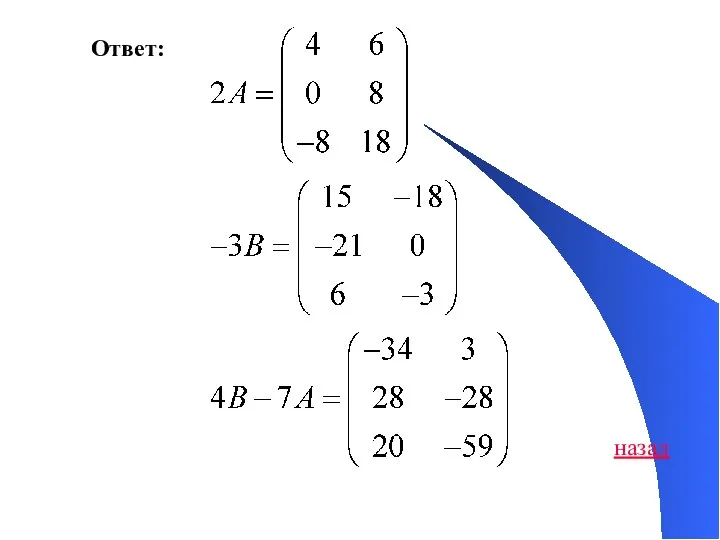
- 44. Ответ: назад
- 45. Пример Ответ назад
- 46. Ответ: назад
- 48. Скачать презентацию








































 Сложение чисел с переходом через десяток в пределах 20
Сложение чисел с переходом через десяток в пределах 20 Преобразования графиков
Преобразования графиков История одной задачи
История одной задачи Исследование операций. Теория игр. Лекция 8
Исследование операций. Теория игр. Лекция 8 Математическое путешествие в мир гармонии. Устный журнал
Математическое путешествие в мир гармонии. Устный журнал Решение заданий олимпиады ПРОФИ 2017
Решение заданий олимпиады ПРОФИ 2017 Подготовка к ГИА по математике. Задания 8
Подготовка к ГИА по математике. Задания 8 Логические задачи. 1 класс
Логические задачи. 1 класс Задача о поиске устойчивых паросочетаний. (Лекция 11)
Задача о поиске устойчивых паросочетаний. (Лекция 11) Свойство параллельности
Свойство параллельности Изучить понятия параллельное проектирование и его
Изучить понятия параллельное проектирование и его Действие умножение
Действие умножение 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Логарифмы вокруг нас
Логарифмы вокруг нас Тема 4. Производная функции
Тема 4. Производная функции Косинус угла
Косинус угла Многочлены над числовыми полями
Многочлены над числовыми полями Своя игра. Натуральные числа
Своя игра. Натуральные числа Теорема косинусов
Теорема косинусов Разложение многочленов на множители с помощью комбинации различных приёмов
Разложение многочленов на множители с помощью комбинации различных приёмов Сложение двузначных чисел
Сложение двузначных чисел Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Игра - путешествие В стране занимательной математики
Игра - путешествие В стране занимательной математики Угол. Виды углов. Как образовалась эта фигура?
Угол. Виды углов. Как образовалась эта фигура? Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց)
Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց) Квадратичная функция. Её свойства и график
Квадратичная функция. Её свойства и график Интегрированный урок (алгебра + физика). Действия со степенями 8 класс
Интегрированный урок (алгебра + физика). Действия со степенями 8 класс Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021