Содержание
- 2. “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
- 3. Часто знает и дошкольник, Что такое треугольник, А уж вам-то, как не знать… Но совсем другое
- 4. Это интересно Треугольник – простейшая фигура: три стороны, три вершины, три угла. Математики называют его двумерным
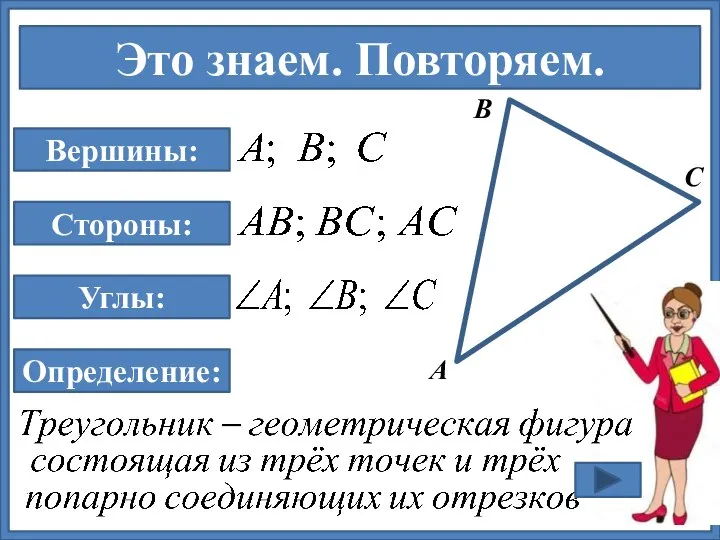
- 5. Это знаем. Повторяем. А В С Вершины: Стороны: Углы: Определение:
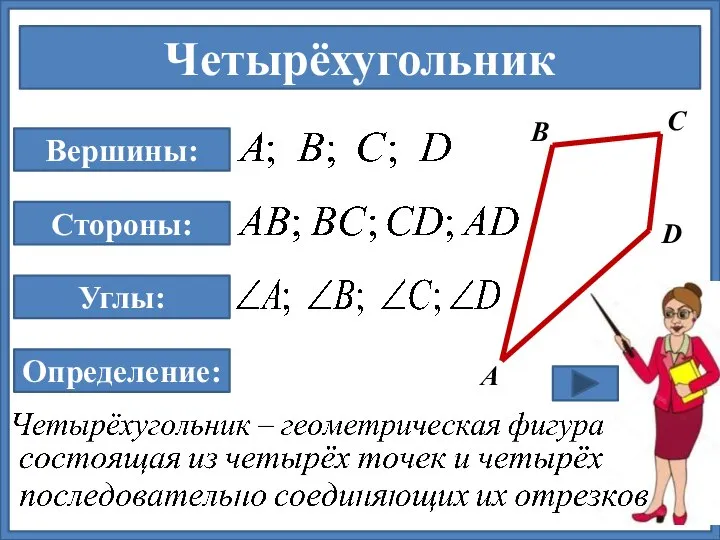
- 6. Четырёхугольник А В С D Вершины: Стороны: Углы: Определение:
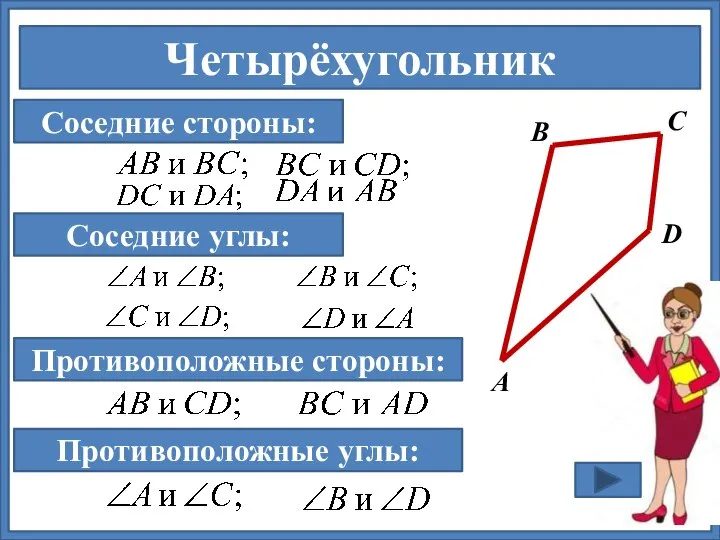
- 7. Четырёхугольник А В С Соседние стороны: Соседние углы: Противоположные стороны: Противоположные углы: D
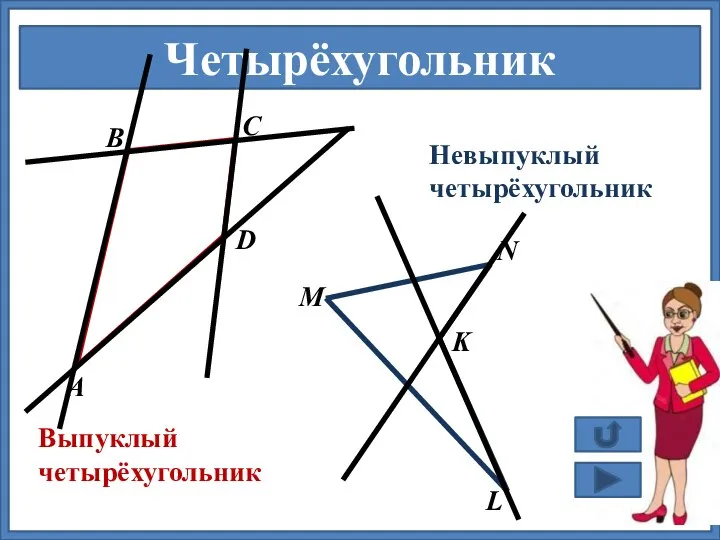
- 8. Четырёхугольник А В С D M N K L Выпуклый четырёхугольник Невыпуклый четырёхугольник
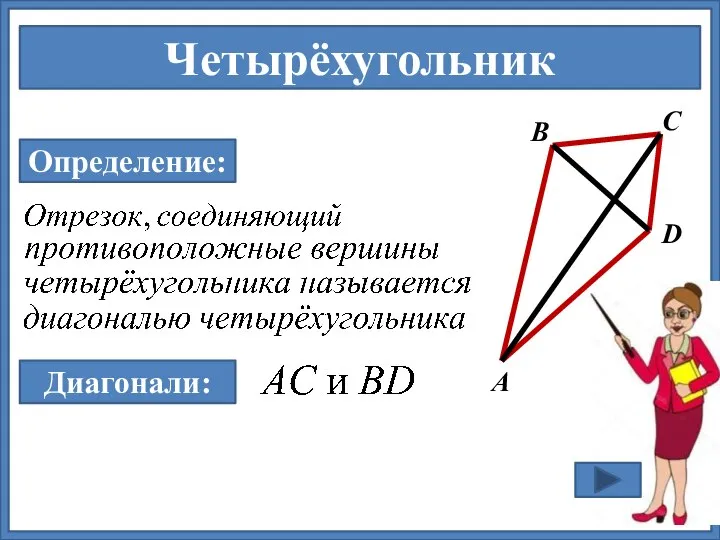
- 9. Четырёхугольник А В С D Определение: Диагонали:
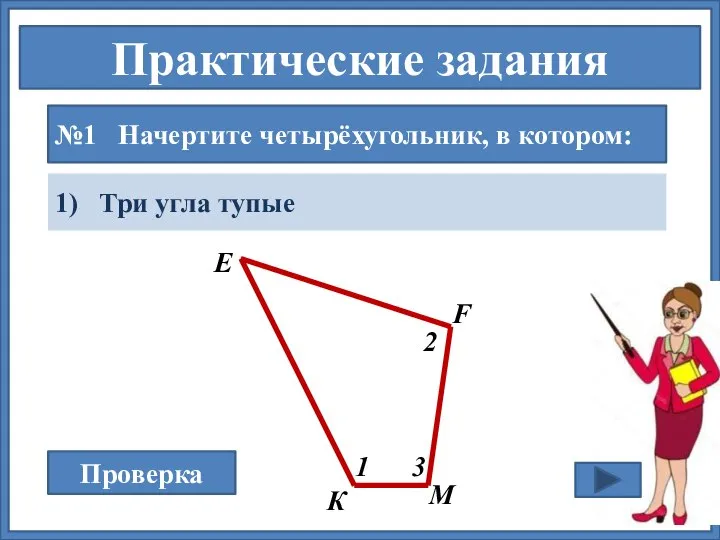
- 10. Практические задания №1 Начертите четырёхугольник, в котором: 1) Три угла тупые М К Е F Проверка
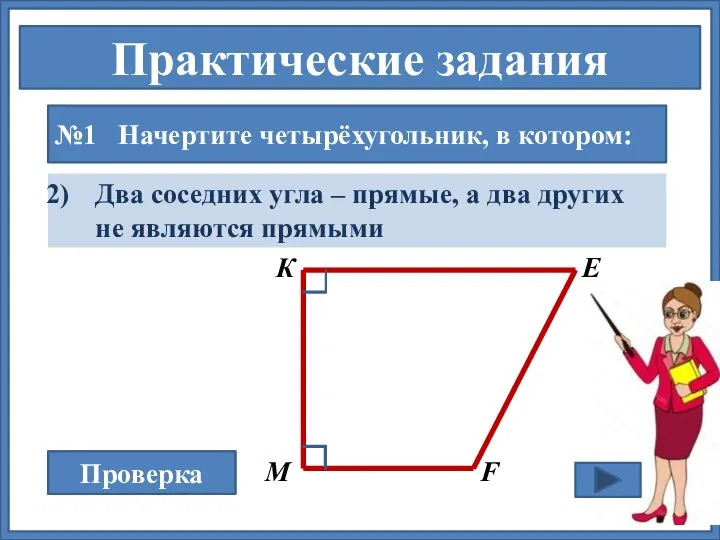
- 11. Практические задания №1 Начертите четырёхугольник, в котором: Проверка Два соседних угла – прямые, а два других
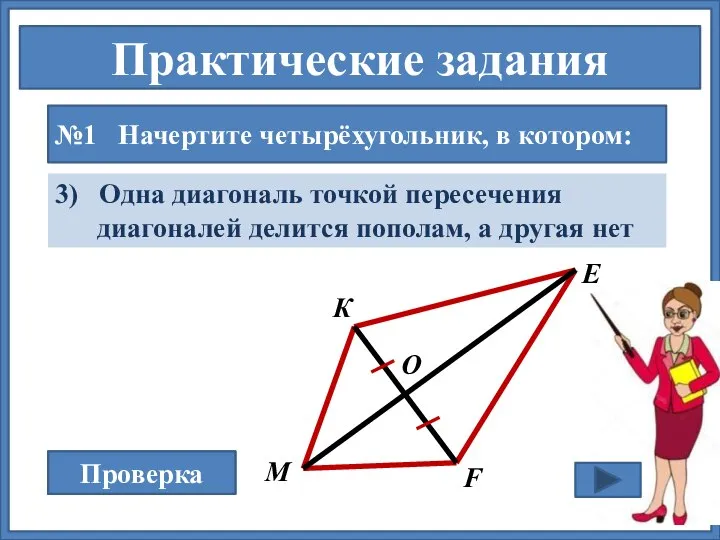
- 12. Практические задания №1 Начертите четырёхугольник, в котором: 3) Одна диагональ точкой пересечения диагоналей делится пополам, а
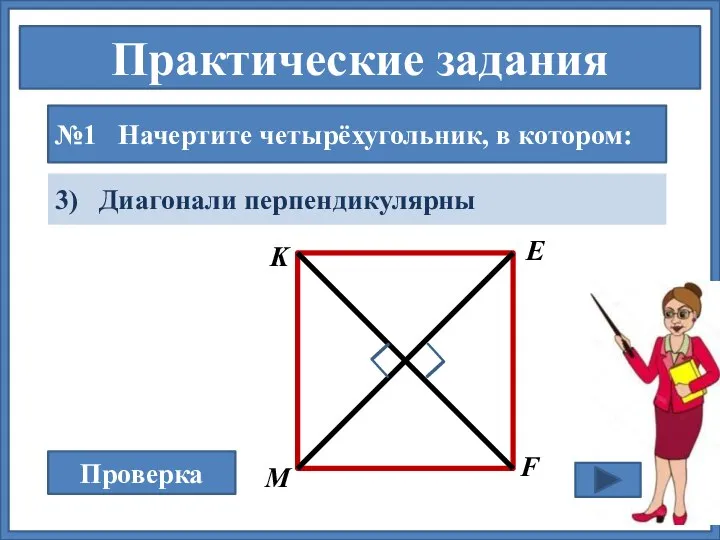
- 13. Практические задания №1 Начертите четырёхугольник, в котором: 3) Диагонали перпендикулярны Проверка М K E F
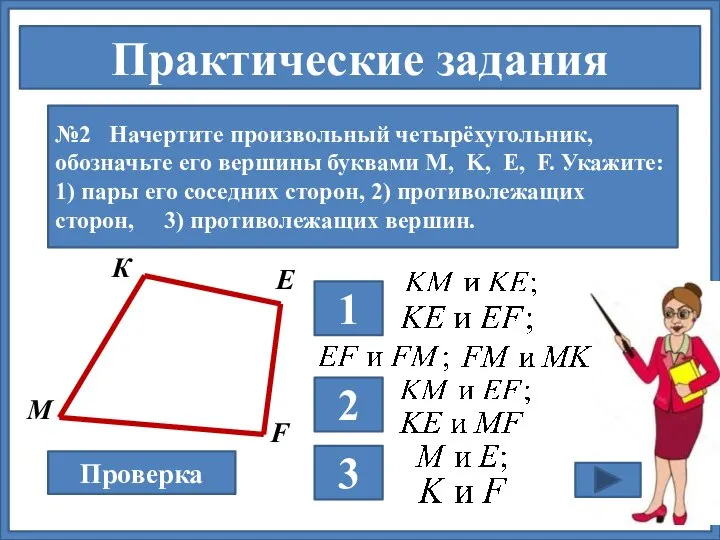
- 14. Практические задания №2 Начертите произвольный четырёхугольник, обозначьте его вершины буквами M, K, E, F. Укажите: 1)
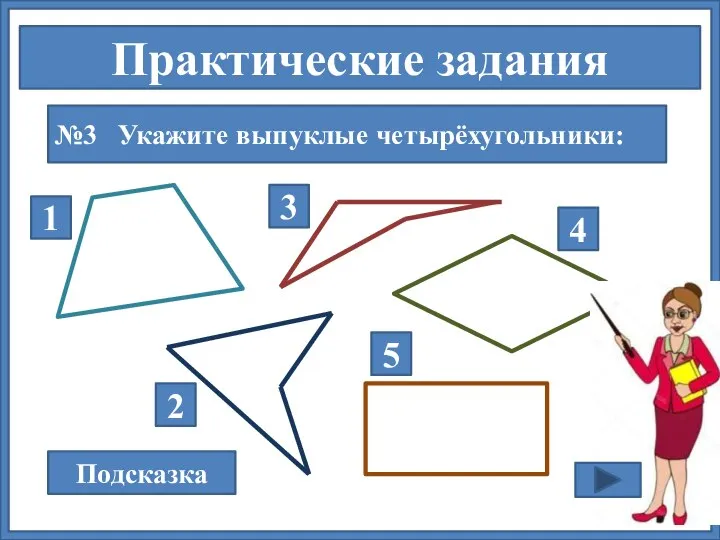
- 15. Практические задания №3 Укажите выпуклые четырёхугольники: Подсказка 1 2 3 4 5
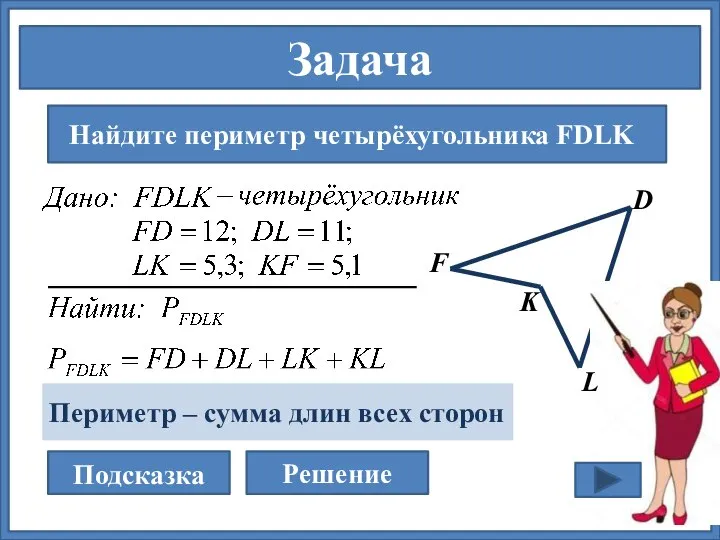
- 16. Задача Найдите периметр четырёхугольника FDLK F D L K Подсказка Решение Периметр – сумма длин всех
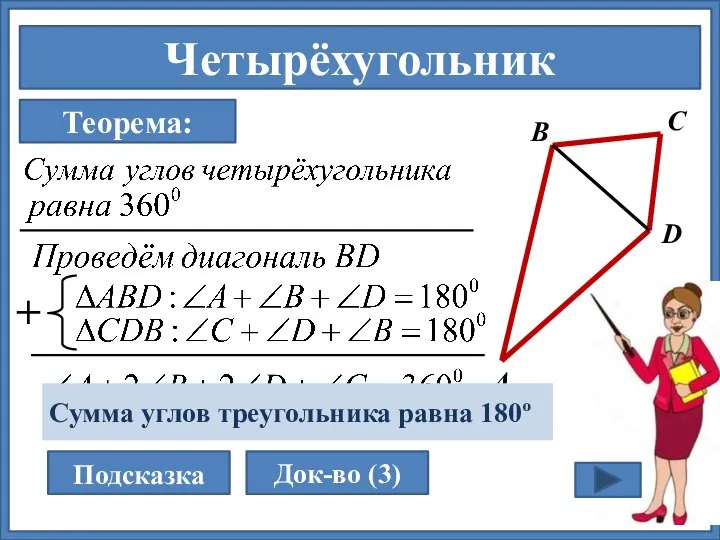
- 17. Четырёхугольник А В С D Теорема: Подсказка Док-во (3) + Сумма углов треугольника равна 180º
- 19. Скачать презентацию



 Квадрат и куб. 4 класс
Квадрат и куб. 4 класс Интеграл
Интеграл Назначение и описание критерия Фишера
Назначение и описание критерия Фишера Показательная функция. Порядок роста и убывания функции
Показательная функция. Порядок роста и убывания функции Аксонометрические проекции
Аксонометрические проекции Пропорция
Пропорция Экономические задачи VI. Задания 1-4, ЕГЭ
Экономические задачи VI. Задания 1-4, ЕГЭ Квадратные корни. 8 класс
Квадратные корни. 8 класс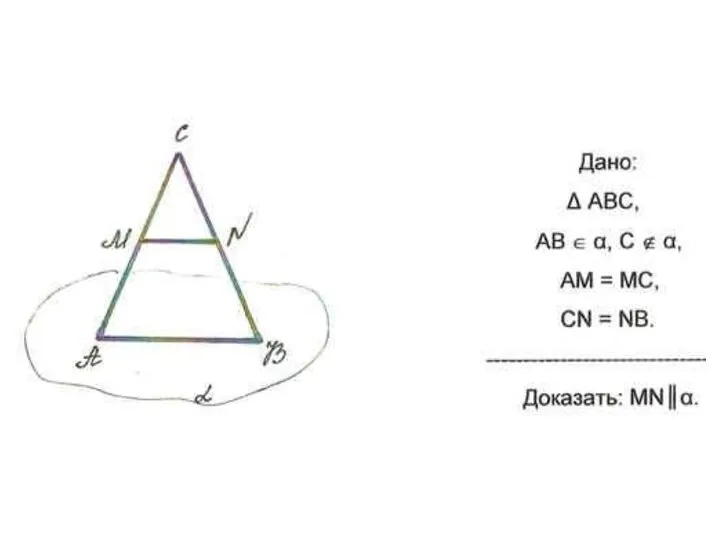 Параллельные прямые. Решение задач
Параллельные прямые. Решение задач Наибольшее и наименьшее значения непрерывной функции на промежутке
Наибольшее и наименьшее значения непрерывной функции на промежутке Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Математика для самых маленьких (младшая группа)
Математика для самых маленьких (младшая группа) Матрицы и определители
Матрицы и определители Практическая работа
Практическая работа Как построить треугольник с помощью циркуля
Как построить треугольник с помощью циркуля Спасение похищенных чисел. Урок-сказка
Спасение похищенных чисел. Урок-сказка Теория вероятностей
Теория вероятностей Операции, функции, выражения
Операции, функции, выражения Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении Показательные уравнения и неравенства
Показательные уравнения и неравенства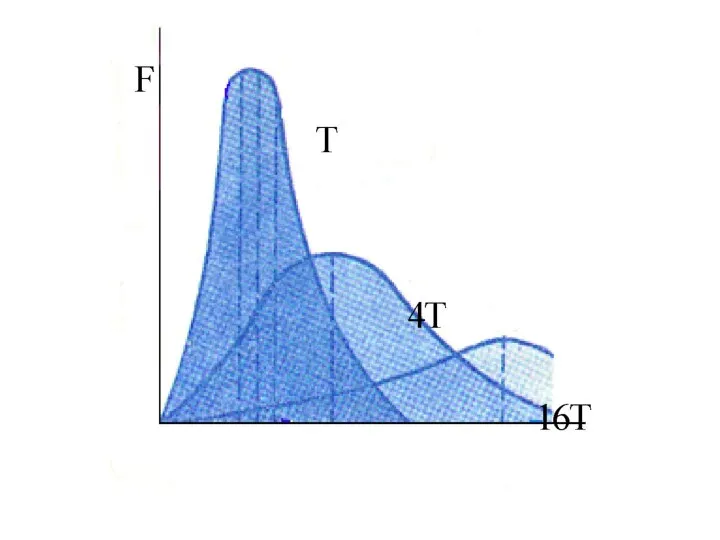 Функция распределения Максвелла
Функция распределения Максвелла Презентация на тему Решение неравенств с одной переменной (11 класс)
Презентация на тему Решение неравенств с одной переменной (11 класс)  Параллельные прямые в пространстве. Урок геометрии в 10 классе
Параллельные прямые в пространстве. Урок геометрии в 10 классе Золотое сечение
Золотое сечение Решение неравенств
Решение неравенств Алгоритмы нахождения независимого множества
Алгоритмы нахождения независимого множества Презентация по математике "Пропорциональные величины" -
Презентация по математике "Пропорциональные величины" -