Пересечение поверхностей

МЕТОД КОНЦЕНТРИЧЕСКИХ СФЕР
Для применения метода концентрических сфер необходимо выполнение трех условий:
1) Обе пересекающиеся поверхности должны быть поверхностями вращения;
2) Оси поверхностей должны пересекаться;
3) Поверхности должны иметь общую плоскость симметрии, т.е.оси поверхностей должны лежать в одной плоскости.

Алгоритм решения.
Находим центр секущих сфер – точку пересечения осей вращения заданных поверхностей.
Находим минимальный радиус сферы (Rmin). Сфера минимального радиуса должна одну поверхность пресекать, а другой касаться, т.е. быть вписанной.
Находим радиус максимальной секущей сферы, она должна проходить через самую дальнюю точку пересечения очерков поверхностей.
Строим линии пересечения сферы Rmin с заданными поверхностями.
Определяем точки пресечения построенных линий.
Произвольно выбираем последовательно ряд промежуточных секущих сфер и повторяем построения по пунктам 4 и 5.
Соединяем точки плавной кривой линией с учетом видимости.

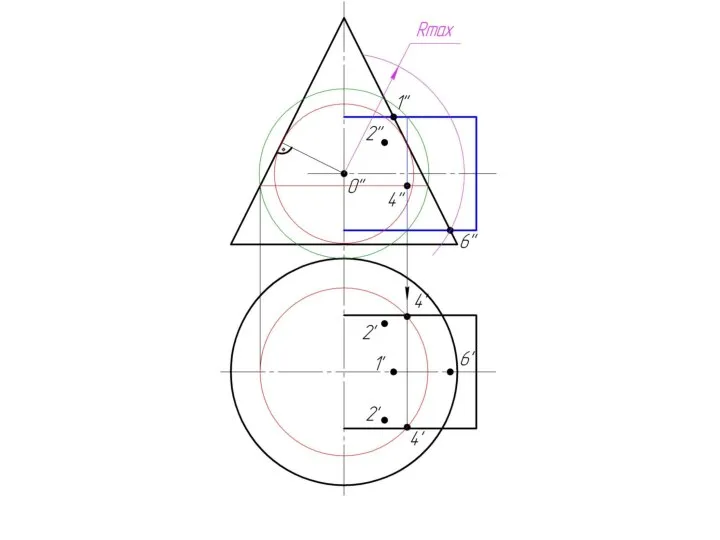
Находим центр секущих сфер –
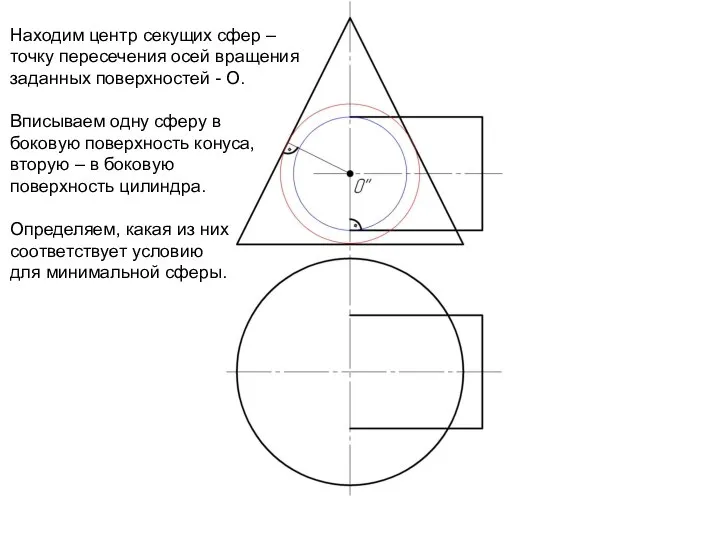
точку пересечения осей вращения заданных поверхностей - О.
Вписываем одну сферу в
боковую поверхность конуса,
вторую – в боковую
поверхность цилиндра.
Определяем, какая из них
соответствует условию
для минимальной сферы.

Находим минимальный радиус
сферы (Rmin).
Сфера минимального радиуса
должна одну поверхность
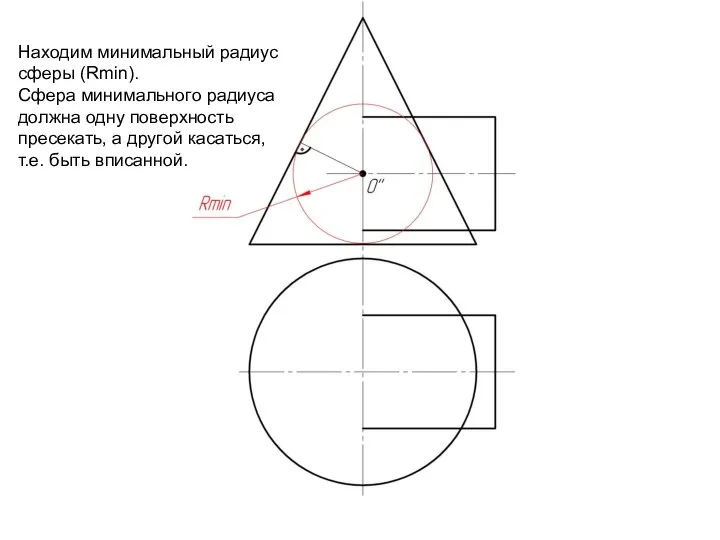
пресекать, а другой касаться,
т.е. быть вписанной.

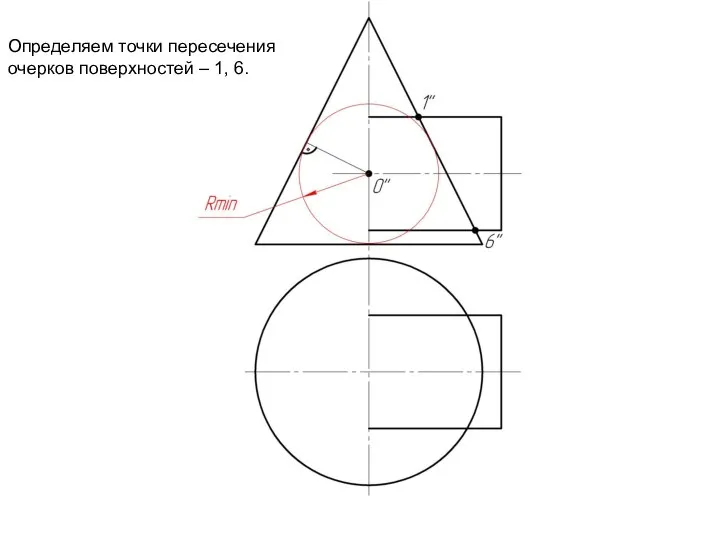
Определяем точки пересечения
очерков поверхностей – 1, 6.

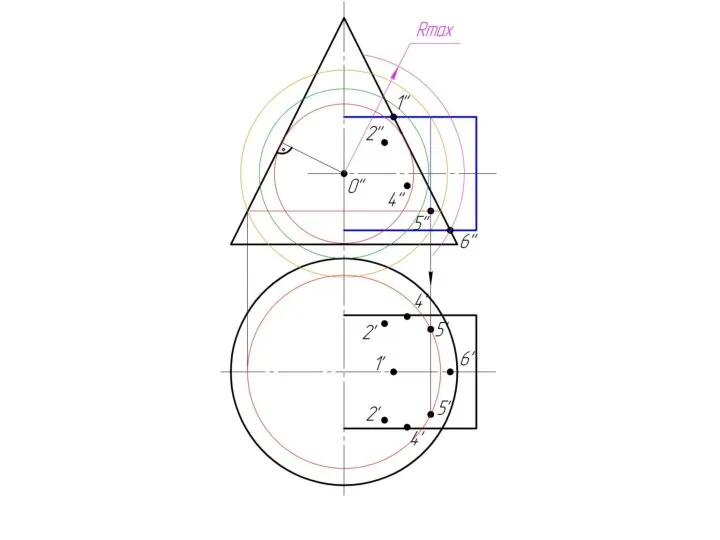
Находим радиус максимальной
секущей сферы, она должна
проходить через самую дальнюю
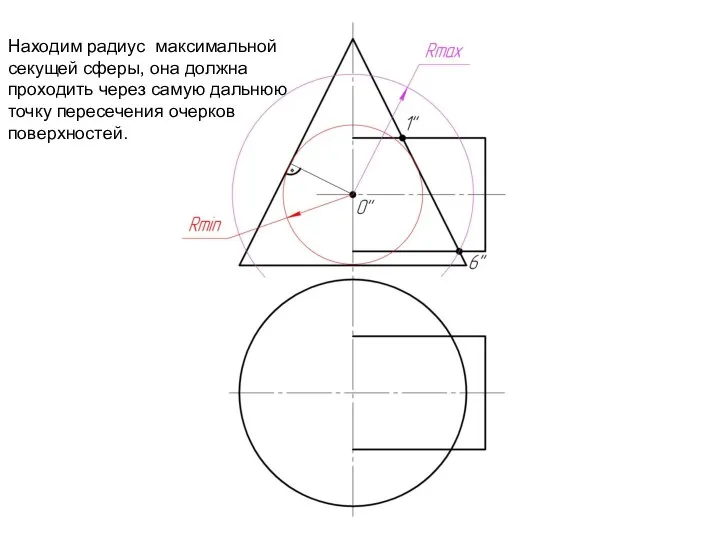
точку пересечения очерков поверхностей.

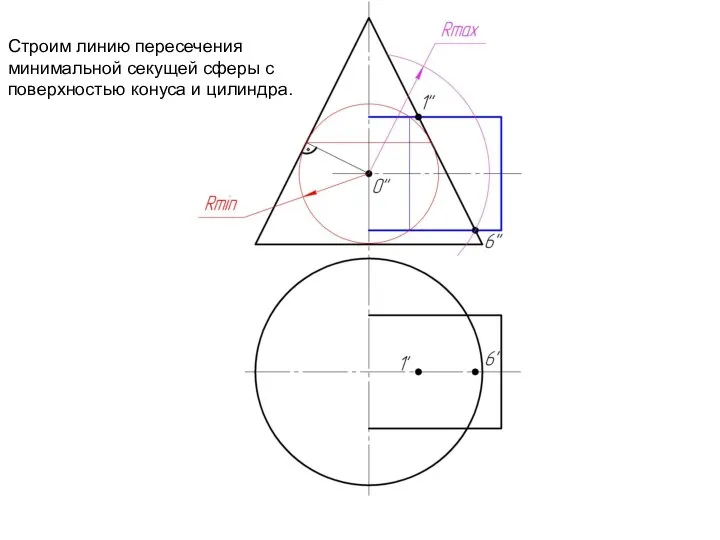
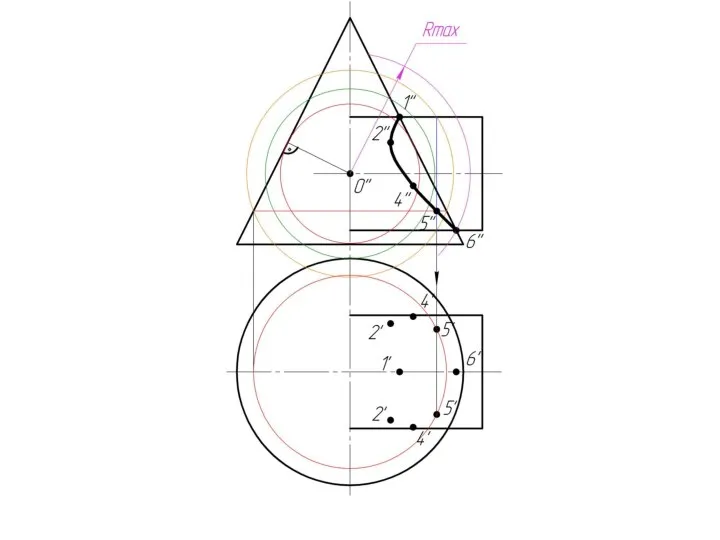
Строим линию пересечения минимальной секущей сферы с
поверхностью конуса и цилиндра.

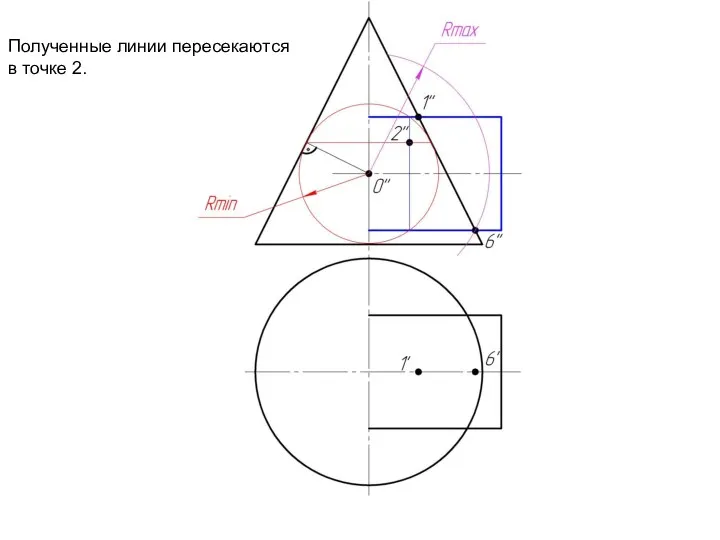
Полученные линии пересекаются
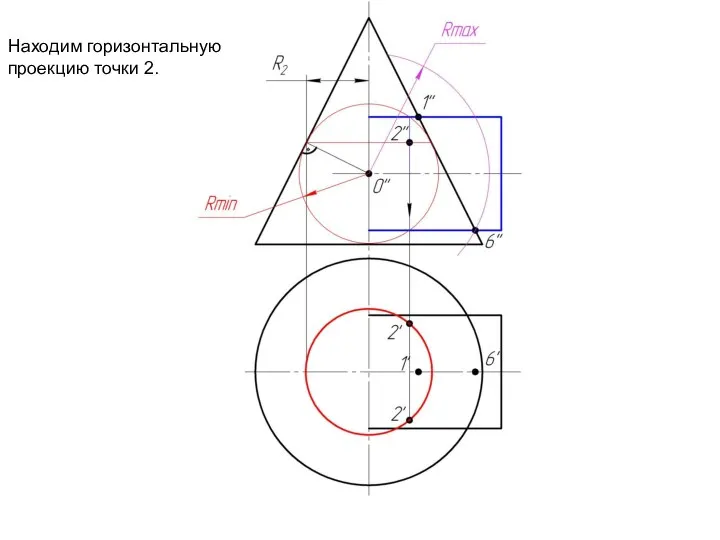
в точке 2.

Находим горизонтальную
проекцию точки 2.

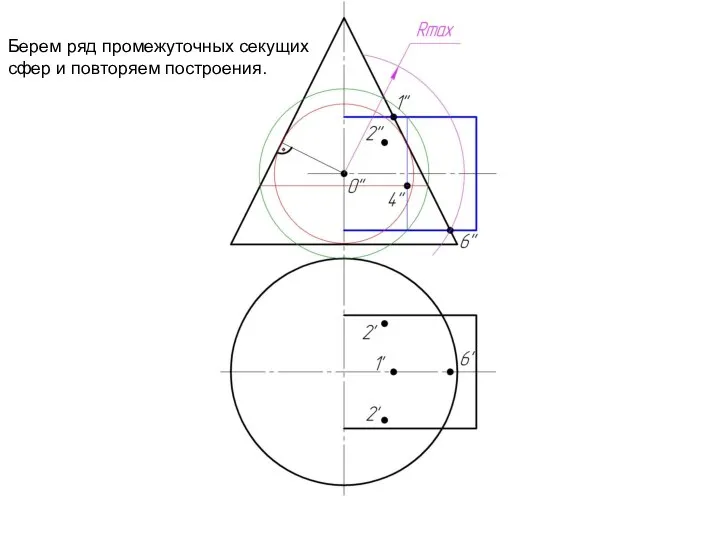
Берем ряд промежуточных секущих
сфер и повторяем построения.