Содержание
- 2. Показательная функция Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим
- 3. Определение. Показательной функцией называется функция y=ax, где а – заданное число, а>0, а≠1.
- 4. Свойства показательной функции 1. Область определения показательной функции – множество R всех действительных чисел. 2. Множество
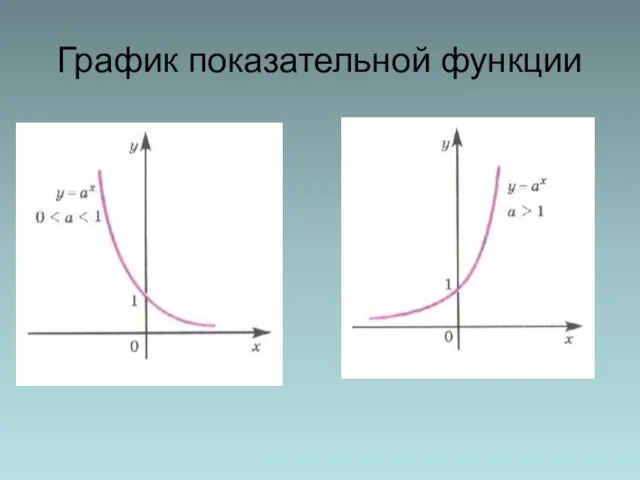
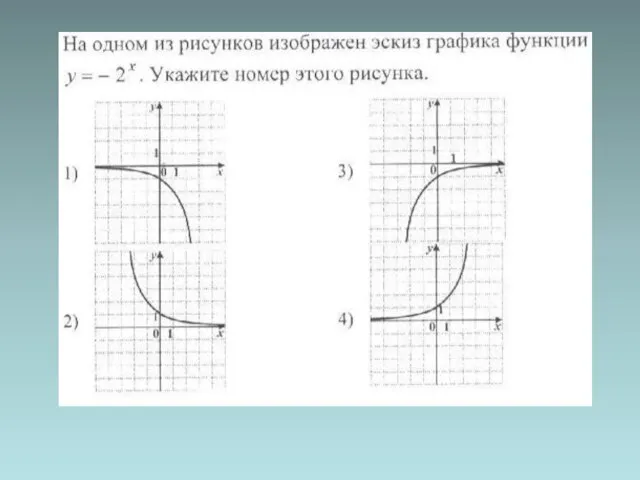
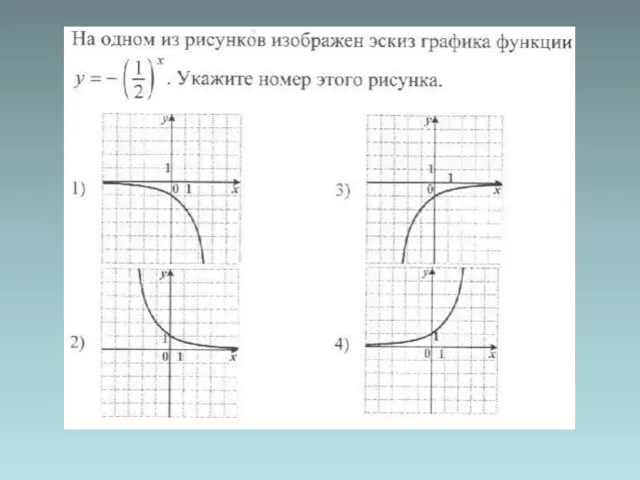
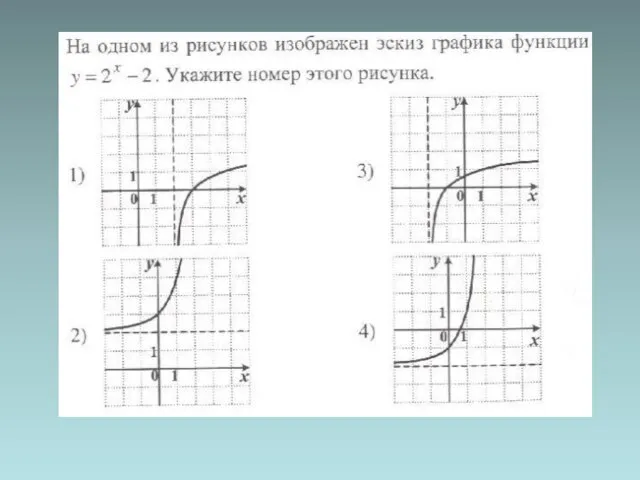
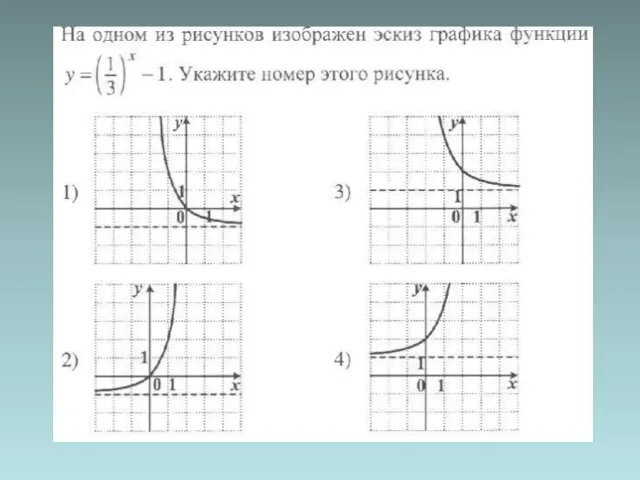
- 5. График показательной функции
- 6. Сравнение чисел Сравните числа: а) 2π и 23,14. Решение. Так как π>3,14 и у=2х возрастает на
- 9. Методы решения показательных уравнений 1. Ответ x= -3
- 10. 2.
- 11. 3.
- 12. 4.
- 13. 5.
- 14. 6.
- 15. 7.
- 16. 8.
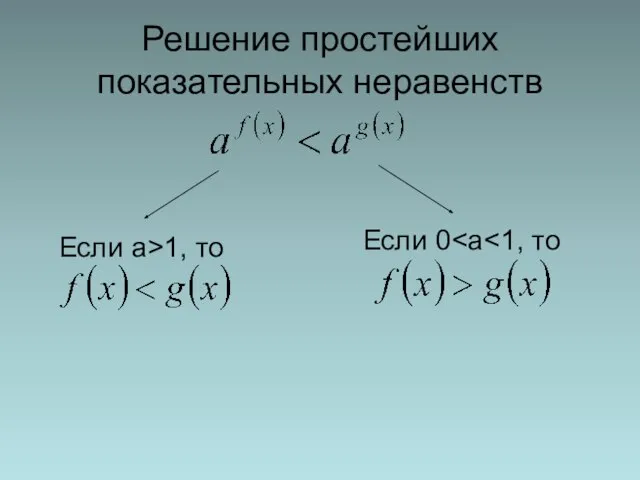
- 17. Решение простейших показательных неравенств Если а>1, то Если 0
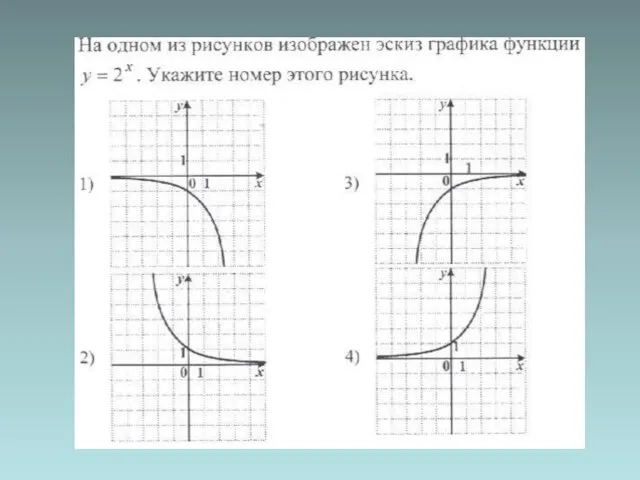
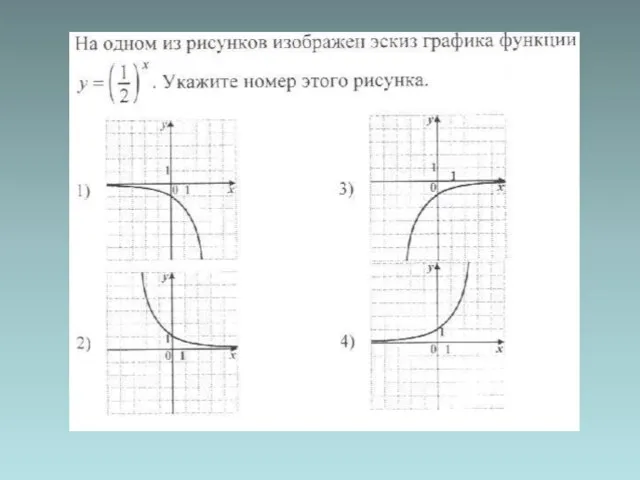
- 18. Графики показательной функции
- 26. Скачать презентацию















 Дәрігердің деонтологиясы
Дәрігердің деонтологиясы Массаж , виды массажа и влияние массажа на функциональное состояние организма
Массаж , виды массажа и влияние массажа на функциональное состояние организма Клебсиеллалар, микоплазмалар. Сипаттамасы. Қасиеттері. Диагноз қою, алдын алу, емдеу
Клебсиеллалар, микоплазмалар. Сипаттамасы. Қасиеттері. Диагноз қою, алдын алу, емдеу Бинтовые повязки. Краткосрочные курсы
Бинтовые повязки. Краткосрочные курсы Сестринское обследование пациентов терапевтического профиля
Сестринское обследование пациентов терапевтического профиля Вирусный гепатит А
Вирусный гепатит А Визначення вмісту консервантів та поживних речовин в продуктах харчування
Визначення вмісту консервантів та поживних речовин в продуктах харчування Ағзаға инсулин еңгізгенде қандай процесс байқалады: гипергликемия, гликогенолиз, гликогеннің глюкозаға ауысуы
Ағзаға инсулин еңгізгенде қандай процесс байқалады: гипергликемия, гликогенолиз, гликогеннің глюкозаға ауысуы Альфа–адреноблокаторы
Альфа–адреноблокаторы Пациент: Беляева Екатерина Николаевна
Пациент: Беляева Екатерина Николаевна Оценка функционального состояния человека. Термометрия. Лихорадка
Оценка функционального состояния человека. Термометрия. Лихорадка Ранний период беременности
Ранний период беременности Артериальная гипертензия
Артериальная гипертензия Перкутанная нефролитотрипсия
Перкутанная нефролитотрипсия Медициналық мекемелер 2 ге бөлінеді. Амбулаториялық. Статционарлық
Медициналық мекемелер 2 ге бөлінеді. Амбулаториялық. Статционарлық Психопатологическая семиотика. Психопатологическая синдромология. Первая помощь при эпилепсии
Психопатологическая семиотика. Психопатологическая синдромология. Первая помощь при эпилепсии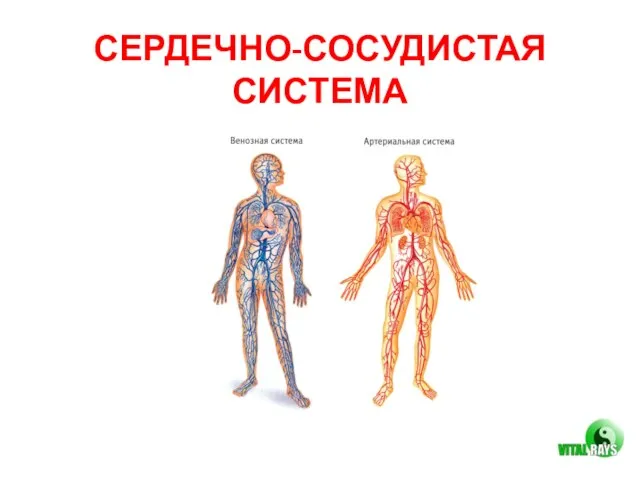 Сердечно-сосудистая система
Сердечно-сосудистая система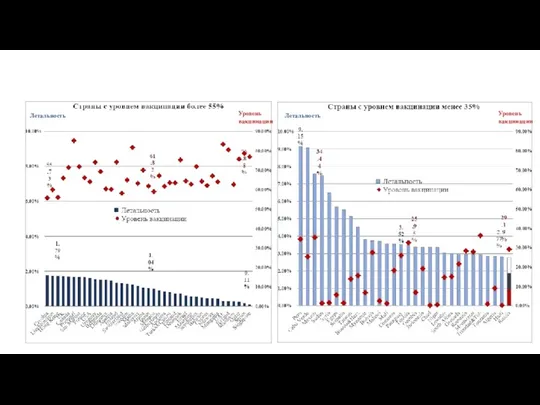 Летальность и вакцинация
Летальность и вакцинация Кишечные бактерии. Сальмонеллы. Шигеллы
Кишечные бактерии. Сальмонеллы. Шигеллы Частная микробиология КожВенЗаболевания. Сифилис
Частная микробиология КожВенЗаболевания. Сифилис Сальмонеллез. Эпидемиология. Клиническая классификация сальмонеллезов
Сальмонеллез. Эпидемиология. Клиническая классификация сальмонеллезов Өкпе артериясының тромбоэмболиясы. Терең көктамырлар тромбозы
Өкпе артериясының тромбоэмболиясы. Терең көктамырлар тромбозы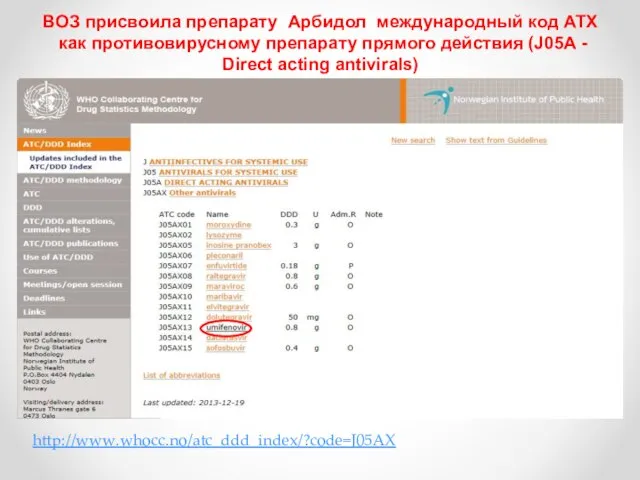 Арбидол. Противовирусная активность Арбидола
Арбидол. Противовирусная активность Арбидола Родовой травматизм матери и плода
Родовой травматизм матери и плода Эндодонтиялық ем жүргізу кезінде қолданылатын коффердам
Эндодонтиялық ем жүргізу кезінде қолданылатын коффердам Суставы: проблемы, профилактика и комплексная терапия заболеваний
Суставы: проблемы, профилактика и комплексная терапия заболеваний Роль сказки при работе в семейном консультировании
Роль сказки при работе в семейном консультировании Zanyatie_1_tverdye_myagkie_lek_formy
Zanyatie_1_tverdye_myagkie_lek_formy