Аттестационная работа. Невозможное возможно

«НЕВОЗМОЖНОЕ ВОЗМОЖНО!»

«КРАСОТА ПРИВЛЕКАЕТ,
ИССЛЕДОВАНИЕ УВЛЕКАЕТ»

Фрактальные невозможные фигуры, созданные Камероном Брауном

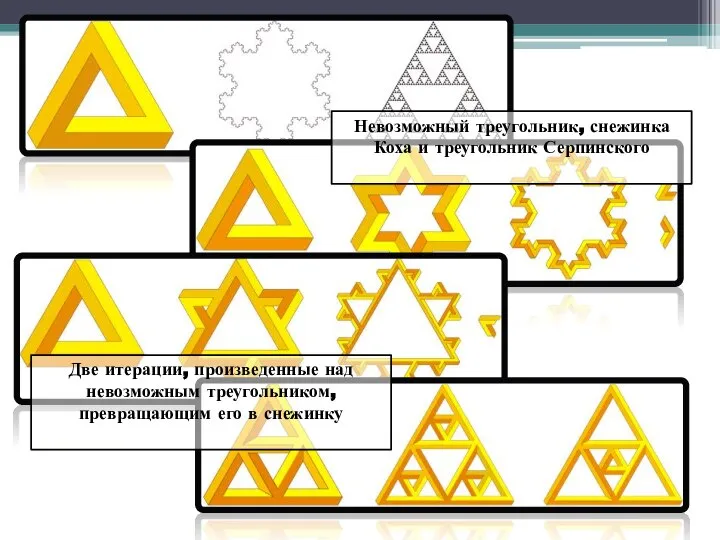
Невозможный треугольник, снежинка Коха и треугольник Серпинского
Две итерации, произведенные над невозможным треугольником, превращающим его в снежинку

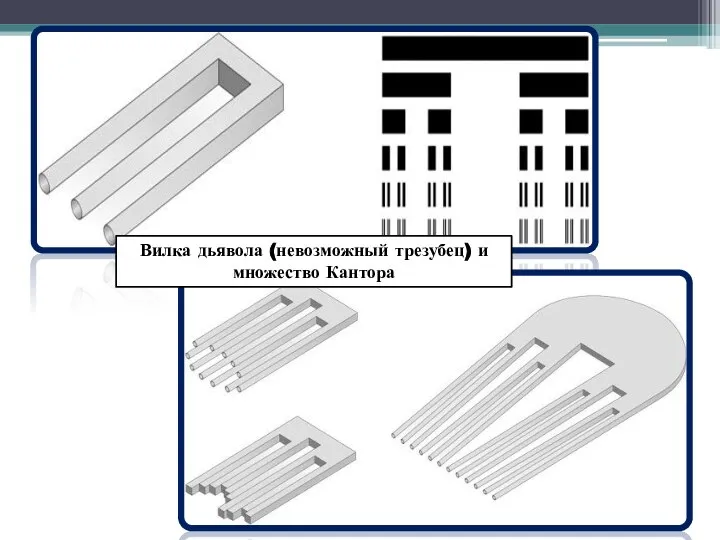
Вилка дьявола (невозможный трезубец) и множество Кантора

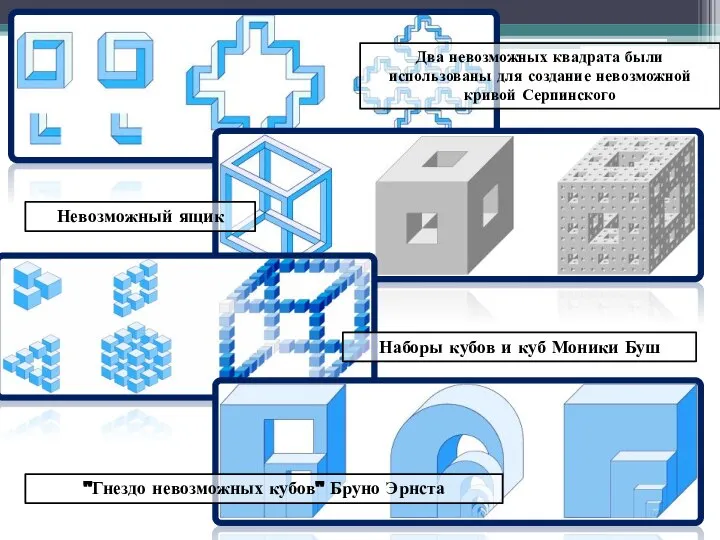
Два невозможных квадрата были использованы для создание невозможной кривой Серпинского
Невозможный ящик
Наборы кубов и куб Моники Буш
"Гнездо невозможных кубов" Бруно Эрнста

Невозможная кривая

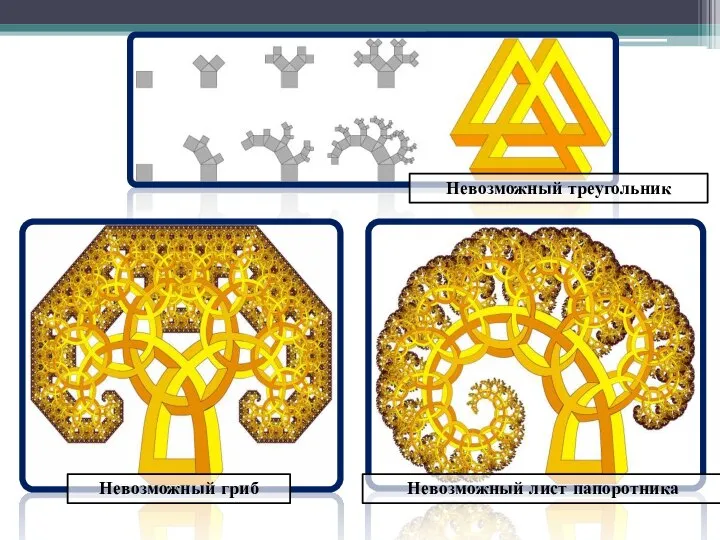
Невозможный гриб
Невозможный треугольник
Невозможный лист папоротника

Спиралевидный треугольник и шестиугольные изометрические спирали

Как вы думаете , чем же актуальны фракталы?

Бенуа Мандельброт
фр. Benoît B. Mandelbrot
Дата рождения:
20 ноября 1924-14 октября 2010
Научная сфера:
фрактальная геометрия

МНОЖЕСТВО МАНДЕЛЬБРОТА
И ЖЮЛЕА

БАССЕЙН НЬЮТОНА

ТРЕУГОЛЬНИК (ПИРАМИДА) СЕРПИНСКОГО

КОВЁР СЕРПИНСКОГО

КРИВАЯ ,СНЕЖИНКА КОХА

КРИВАЯ ПЕАНО

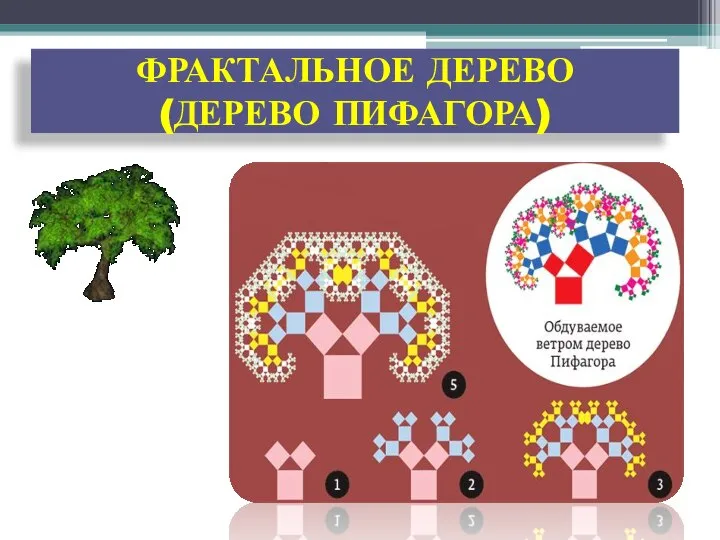
ФРАКТАЛЬНОЕ ДЕРЕВО
(ДЕРЕВО ПИФАГОРА)

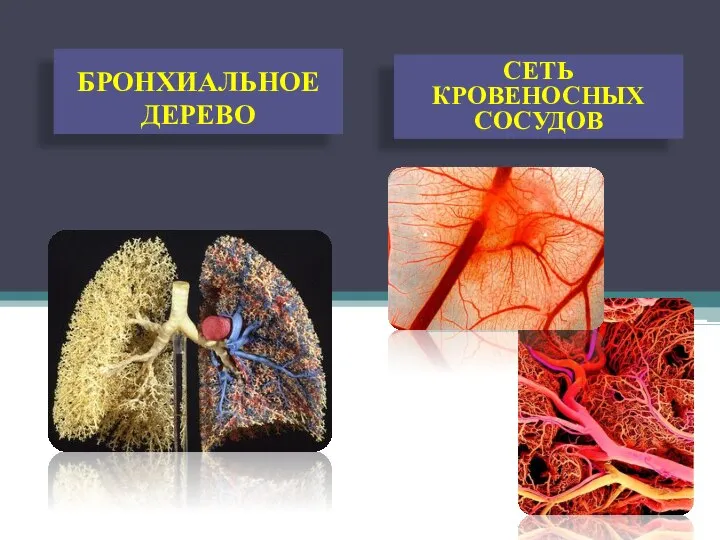
БРОНХИАЛЬНОЕ ДЕРЕВО
СЕТЬ КРОВЕНОСНЫХ СОСУДОВ

МОЛНИЯ
КАПУСТА БРОКОЛЛИ

ФРАКТАЛЬНЫЕ АНТЕННЫ
(фракталы в радиотехнике)

ФРАКТАЛЫ В ИНФОРМАТИКЕ

ФРАКТАЛЫ В ЭКОНОМИКЕ

ФРАКТАЛЫ В НАРОДНОМ ТВОРЧЕСТВЕ

ФРАКТАЛЫ В КУЛИНАРИИ

ФРАКТАЛЫ В ИНТЕРЬЕРЕ

Лист Мебиуса – символ математики,
Что служит высшей мудрости венцом…
Он полон неосознанной романтики:
В нем бесконечность свернута кольцом.
В нем – простота, и вместе с нею – сложность,
Что недоступна даже мудрецам:
Здесь на глазах преобразилась плоскость
В поверхность без начала и конца.
Здесь нет пределов, нет ограничений,
Стремись вперед и открывай миры,
Почувствуй силу новых ощущений,
Прими познанья высшего дары…

Август Фердинанд Мёбиус
August Ferdinand Möbius
Дата рождения:
17 ноября 1790-26 сентября 1868
Место рождения:
Шульпфорте, курфюршество Саксония
Научная сфера:
математика, астрономия

А в то же время…
Одновременно с Мёбиусом изобрел этот лист и другой ученик К. Ф. Гаусса —
Иоганн Бенедикт Листинг
(1808— 1882),
профессор Геттингенского университета.
Свою работу он опубликовал на три года раньше,
чем Мёбиус,— в 1862 году
А называется лента именем Мёбиуса

Лента Мёбиуса
Что произойдет, если разрезать по центральной линии ленту Мебиуса?
Сколько она имеет поверхностей:
одну или две?
А если красить по поверхности, то лента закрасится с одной стороны или с двух?

Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным.
Блез Паскаль

МАСТЕР-КЛАСС

Основополагающий вопрос :
Можно ли подержать бесконечность в своих руках?

Эксперименты
с бумагой

Берем бумажную ленту АВСD. Прикладываем ее концы АВ и СD друг к другу и склеиваем. Но не как попало, а так, чтобы точка А совпала с точкой С, а точка B с точкой D.
А
В
С
D

Получим перекрученное кольцо

ВОПРОС №1:
сколько сторон у этого куска бумаги? Две, как у любого другого?
У него ОДНА сторона. Не верите?
Хотите – проверьте: попробуйте провести линию на этом кольце с одной стороны.

Проводим линию,
не отрываемся, на другую сторону не переходим. Провели?
А где же вторая, чистая сторона?
Нет?

ВОПРОС №2:
Что будет, если разрезать обычный лист бумаги?
Конечно же, два обычных листа бумаги. Точнее, две половинки листа.
А что случится, если разрезать вдоль посередине это кольцо (это и есть лист Мёбиуса, или лента Мёбиуса) по всей длине?
Два кольца половинной ширины?
А что? Разрежьте сами.

А вот что получилось …
Лента перекручена два раза

Теперь сделайте новый лист Мёбиуса
и скажите, что будет,
если разрезать его вдоль, но не посередине,
а ближе к одному краю?
То же самое?

А вот что получилось …

А если на три части?
Сколько получится лент?
Три ленты?

Получим два сцепленных кольца.
Одно из них вдвое длиннее исходного и перекручено два раза.
Второе- лист Мёбиуса, ширина которого втрое меньше, чем у исходного.

Эксперименты
с веревкой и жилетом

Есть гипотеза, что
спираль ДНК
сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия.
Такая структура вполне логично объясняет причину наступления биологической смерти –
спираль замыкается сама на себя и происходит самоуничтожение.

Обычная бутылка Клейна
Многослойная бутылка Клейна
БУТЫЛКА КЛЕЙНА

В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
В 1971 году изобретатель Чесноков П.Н. применил фильтр в виде листа Мёбиуса.

Международный символ переработки

Главной ландшафтной метафорой на «Сибирской ярмарке» стала лента Мебиуса, предложенная дизайнерами

В ИНТЕРЬЕРЕ

Лист Мёбиуса в литературе
Лента Мебиуса - любимый объект фантастических рассказов. В одном из них, например, пропал поезд нью-йоркского метро. Оказалось, что один из маршрутов пролегал по ленте Мебиуса, и поезд затерялся во времени.

Лист Мёбиуса в астрономии
Существует гипотеза что наша вселенная устроена в форме листа Мебиуса

Свойства односторонностей листа Мёбиуса было использовано в технике:
1. Если у релейной передачи ремень сделать в виде ленты Мёбиуса, то его поверхность будет изнашиваться в да раза медленнее чем у обычного кольца, в работе ремня принимает участие вся поверхность, а не только внутренняя ее часть, как у обычной ременной передачи.
2. Были созданы особые кассеты для магнитофона, которые дали возможность слушать магнитофонные кассеты “с двух сторон”, не меняя их местами.
3. Абразивные ремни для заточки инструментов
4. В матричных принтерах красящая лента имела вид ленты Мёбиуса
5. А лет 18 назад лента стала использоваться как пружина
В ТЕХНИКЕ

Лист Мёбиуса –
жёлтая страница,
Односторонний сказочный маршрут,
Летит метелью, песенкой, синицей,
Бульварной лентой склеенный маршрут.
Эх, Мёбиус, спасибо за науку!
Поверхность одинокой стороны
Подобна заколдованному звуку,
Вибрирующей неоновой струны

ВЫВОД
Лист Мёбиуса –
удивительный феномен.
Его можно исследовать до бесконечности, мы рассмотрели лишь некоторые его свойства.
Надеемся, что мы вас заинтересовали и вы продолжите исследования этого непредсказуемого листа.

Лист Мебиуса имеет один край, одну сторону
Лист Мёбиуса - топологический объект. Как и любая топологическая фигура, он не меняет своих свойств, пока его не разрезают, не разрывают или не склеивают его отдельные куски.
Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.
Лист Мёбиуса находит многочисленные применения в кулинарии, в технике, в физике, в живописи, в архитектуре, в оформлении ювелирных изделий и бижутерии.
Лента Мебиуса вдохновляет многих художников на создание известных скульптур и картин.
Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.
СВОЙСТВА ЛИСТА МЕБИУСА

ИНТЕЛЛЕКТ-КАРТА