«Московский государственный университетимени М. В. Ломоносова»   Экономический факультет   ПРЕЗЕНТАЦИЯ К ВЫПУСКНОЙ КВАЛИФИКАЦИ

Давайте посмотрим, в каком мире нам с Вами предстоит жить. Что я имею ввиду в первую очередь, конечно это то, что очень тяжело предсказать, что будет в будущем. В начале 2008г. большинство аналитиков с Wall Street мало могли себе представить то, что будет в конце этого же года!

John K. Galbrith (1908–2006)
однажды сказал: «Единственная функция экономического прогнозирования – это заставить уважать астрологию». Т.е. в нашем быстроменяющемся мире очень трудно или почти невозможно предсказать, что будет в будущем. Мы не знаем, что день грядущий нам готовит.

Целью же данной работы является с помощью эконометрических методов выявить фундаментальные факторы, которые влияют на доходность фьючерса нефти сорта Brent, а также возможность использования применяемых моделей, в целях дальнейшего прогнозирования. Для анализа используются такие известные эконометрические модели как: МНК, ARMA, ARCH-CARCH. Также, в работе рассмотрено возможное влияние на доходность фьючерса на нефть марки Brent других активов, и в частности таких как: стоимость фьючерса на нефть сорта WTI, значение индекса S&P 500, а также данные по добыче нефти, производственным мощностям и ряд других.

Тема исследования видится автору весьма актуальной, особенно касаемо Российской экономики. Как-бы это не казалось негативным, но именно цены на энергоносители, являются основным источником для пополнения бюджета России, да и в целом очень сильно влияют, или лучше сказать влияли, на наш экономический рост. В последнее время все больше экономистов ставят во главу угла не сырьевой рост Российской экономики, но энергоносители еще долго будут оказывать существенное влияние на нашу экономику. Соответственно встает вопрос об основных факторах, которые способствуют ценообразованию на сырьевых рынках. Учитывая тот факт, что цена на основной сорт Российской нефти сорта Urals, напрямую зависит от цен на нефть сорта Brent, в данной работе анализируется именно доходность на фьючерс этой нефти.

Анализ представлен за разные периоды и разные интервалы. За период с января 2000г. по март 2012г., с использованием данных за месяц. Кроме данных с месячным интервалом, проводится анализ данных с дневным интервалом за период с 01.01.2008 по 31.12.2011.
В работе учтен финансовый кризис, который имеет свое начало в 2007 году и который внес существенный вклад в стоимость соответствующих активов.

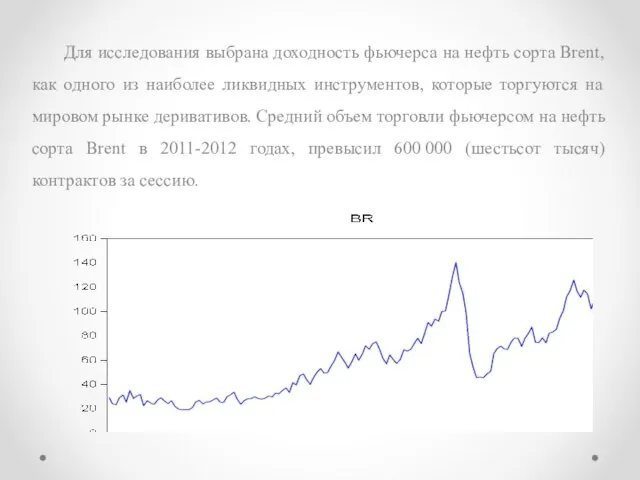
Для исследования выбрана доходность фьючерса на нефть сорта Brent, как одного из наиболее ликвидных инструментов, которые торгуются на мировом рынке деривативов. Средний объем торговли фьючерсом на нефть сорта Brent в 2011-2012 годах, превысил 600 000 (шестьсот тысяч) контрактов за сессию.

В разделе, исследование временных рядов, проведен анализ временных рядов. В ходе анализа исследуются описательные статистики, протестированы ряды на наличие единичного корня и соответственно выясняется, являются ли они стационарными.
Входе анализа было выяснено, что большинство изначальных рядов являются нестационарными. Однако с помощью первой разности, большинство из них становятся стационарными. В свою очередь ряды доходностей, изначально являются стационарными рядами.

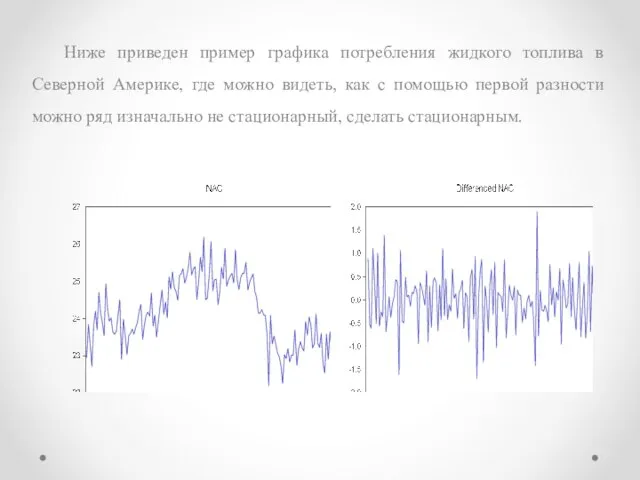
Ниже приведен пример графика потребления жидкого топлива в Северной Америке, где можно видеть, как с помощью первой разности можно ряд изначально не стационарный, сделать стационарным.

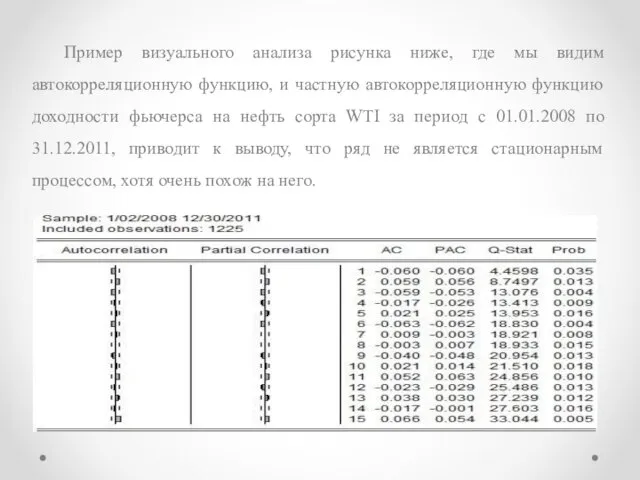
Пример визуального анализа рисунка ниже, где мы видим автокорреляционную функцию, и частную автокорреляционную функцию доходности фьючерса на нефть сорта WTI за период с 01.01.2008 по 31.12.2011, приводит к выводу, что ряд не является стационарным процессом, хотя очень похож на него.

Следующие тесты также проверяют на наличие единичного корня. Это расширенный тест Дики–Фуллера (ADF). Еще один очень часто используемый тест, тест Филлипса–Перрона (PP). Оба теста проверяют нулевую гипотезу о нестационарности процесса при альтернативной гипотезе о том, что процесс стационарен. Тест Филлипса–Перрона учитывает возможность гетероскедастичности ошибок, что может пригодиться при исследовании моделей типа ARCH.

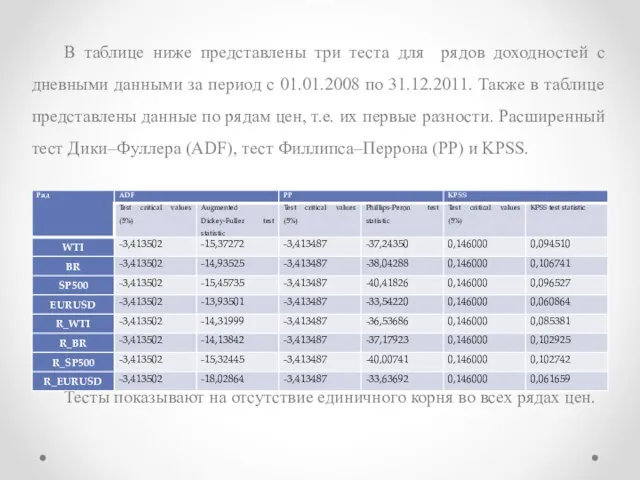
В таблице ниже представлены три теста для рядов доходностей с дневными данными за период с 01.01.2008 по 31.12.2011. Также в таблице представлены данные по рядам цен, т.е. их первые разности. Расширенный тест Дики–Фуллера (ADF), тест Филлипса–Перрона (PP) и KPSS.
Тесты показывают на отсутствие единичного корня во всех рядах цен.

Перед тем, как оценивать модели нескольких временных рядов, проверим наличие истинной/ложной регрессии. Первым шагом будет оценка обычной регрессии. Если регрессия не значима, то значит, между рядами нет зависимости. Если же, регрессия значима и ряды стационарны, то это означает, что регрессия истина. В случаи значимой регрессии и нестационарных рядов переходим ко второму шагу. На втором шагу мы делаем ряды стационарными, например, с помощью первой разности, и снова проверяем на значимость. Если регрессия значимая, то она истинная, если же не значимая, то ложная.
Еще одним тестом на зависимость между рядами, является тест Гранжера на причинно-следственную зависимость. Идея теста, предложенного в работе (Granger, 1969), проста: если x влияет на y, то изменения x должны предшествовать изменениям y, но не наоборот. Если же обе переменные влияют друг на друга, то, скорее всего, есть другая переменная, влияющая на обе.

Наше исследование показало, что среди таких моделей как: ARCH(1), GARCH(1) и GARCH(1,1), наилучшие показатели у последней.
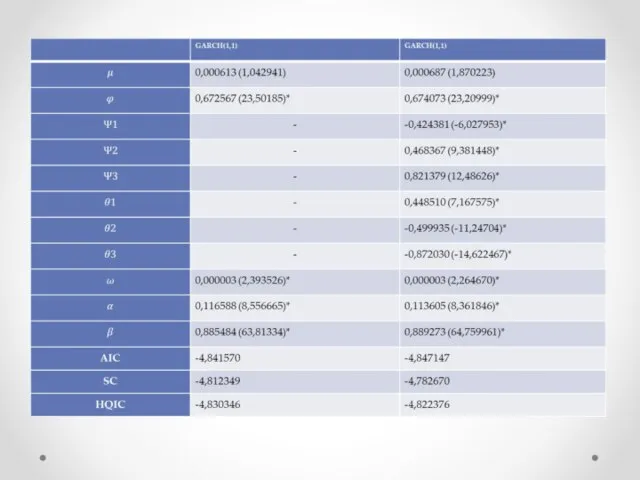
В таблице ниже представлено сравнение двух моделей GARCH за период 01.01.2008 - 31.12.2011, где в качестве зависимой переменной используется доходность фьючерса на нефть сорта Brent, а в качестве независимой доходность курса евро/доллар.
Примечание. В таблице использованы следующие обозначения: μ – константа в уравнении доходности, ψ1 – параметр AR(1) и два три соответственно, θ1 – параметр MA(1) и два три соответственно, φ – параметр доходности фьючерса на нефть сорта Brent, ω – константа в уравнении волатильности, β – параметр “бета” модели GARCH, α – параметр “альфа” модели GARCH. AIC – информационный критерий Акаике, SC – информационный критерий Шварца, HQIC – информационный критерий Ханнана–Куинна. В скобках указаны t-статистики, * обозначает значимость параметра на уровне 5%.