График квадратичной функции Занятие в 9 классе Продолжительность 40 минут Учитель математики Лещенко Любовь Владимировна в
Содержание
- 2. Здравствуйте!
- 3. График квадратичной функции
- 4. Содержание Давайте вспомним График функции у = ах²+ bх + с Справочник
- 5. Алгоритм построения 1.Построим систему координат х0у. 2. Найдем вершину параболы. 3. Построим ось симметрии параболы х
- 6. Некоторые способы нахождения вершины О (х ;у )параболы у=ах²+ bх+с 0 0 0 0 0 0
- 7. Найти координаты вершины параболы у = 2х²- 12х + 14 Выполним преобразования: 2х²- 12х + 14
- 8. Найти координаты вершины параболы у = 2х²- 12х + 14 2х²- 12х + 14 = 0
- 9. Найти координаты вершины параболы у = 2х²- 12х + 14 Используя формулы , Получаем ; 0
- 10. Справочник Определение функции Определение графика функции Вывод формул
- 11. Справочник Функция – это соответствие, при котором каждому элементу одного множества сопоставляется единственный элемент другого множества
- 12. Справочник График числовой функции – множество точек плоскости с координатами (х; f(х)), где х принимает всевозможные
- 13. Вывод формул ; Справочник
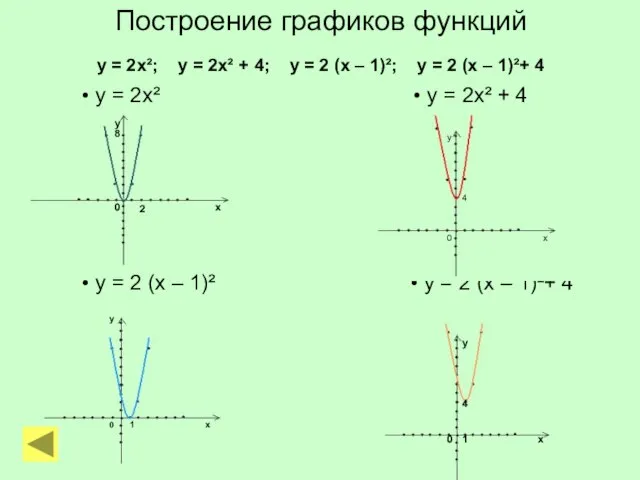
- 14. Постройте графики функций у = 2х²; у = 2х² + 4; у = 2 (х –
- 15. Построение графиков функций у = 2х²; у = 2х² + 4; у = 2 (х –
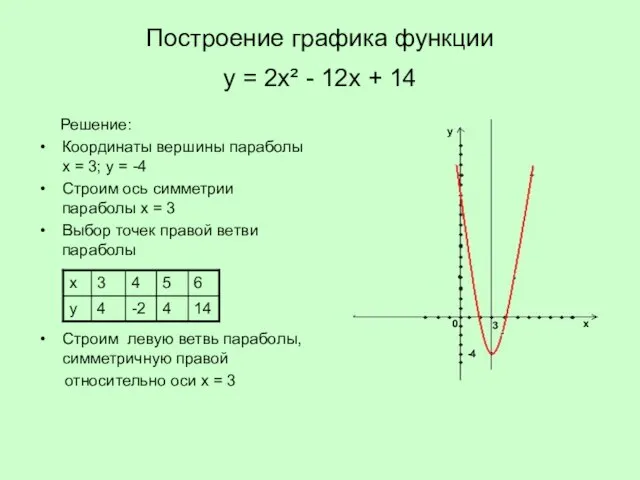
- 16. Постройте график функции у = 2х² - 12х + 14
- 17. Построение графика функции у = 2х² - 12х + 14 Решение: Координаты вершины параболы х =
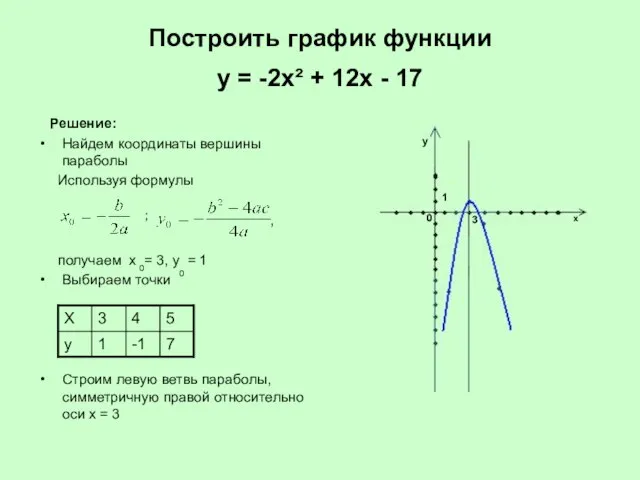
- 18. Построить график функции у = -2х² + 12х - 17 Решение: Найдем координаты вершины параболы Используя
- 19. Домашнее задание Постройте график функции у = 3х² - 2х + 8
- 21. Скачать презентацию














 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр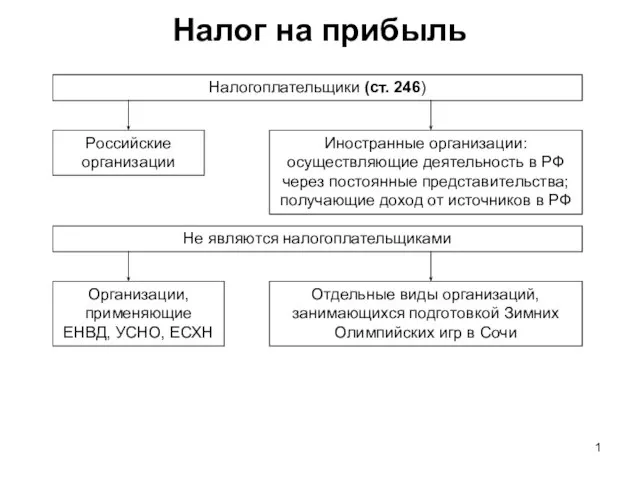 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология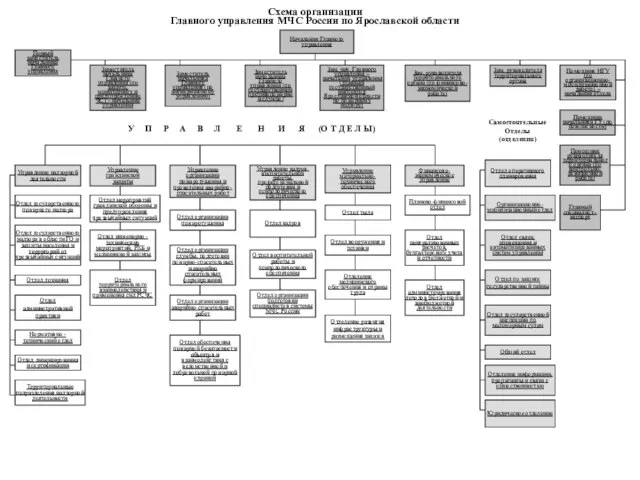 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва