МОУ «ООШ с.Никольское Духовницкого района Саратовской области» Площадь прямоугольника и треугольника Автор: учен

ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию

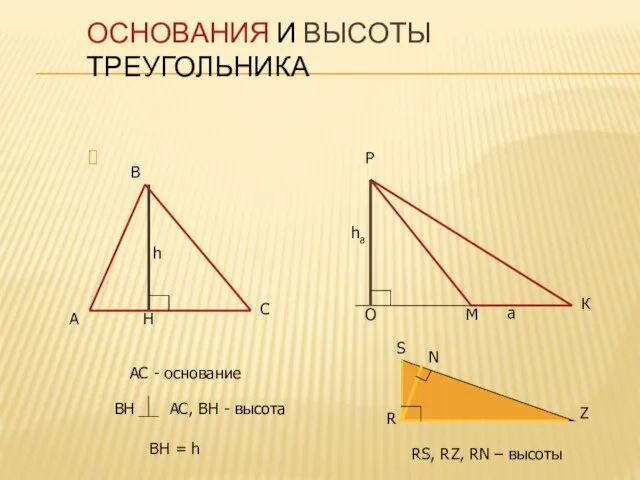
ОСНОВАНИЯ И ВЫСОТЫ ТРЕУГОЛЬНИКА
АС - основание
BH = h
RS, RZ, RN – высоты

ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Теорема: площадь треугольника равна половине
произведения основания на высоту
Доказать: SABC = 1/2 AC ∙ BH
Доказательство:
АВКС – параллелограмм, его снованием является
АС, а высотой является ВН
SABKC = AC ∙ BH
SABKC = SABC + SKCB , SABC = 1/2 SABKC
SABC = 1/2 AC ∙ BH
Треугольники АВС и КСВ равны, значит,
их площади тоже равны

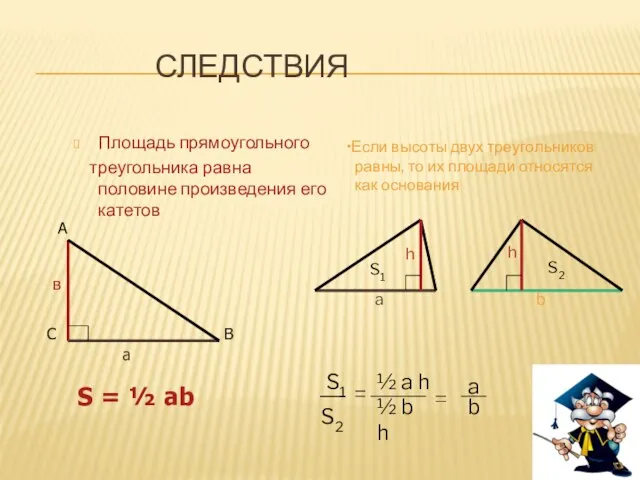
СЛЕДСТВИЯ
Площадь прямоугольного
треугольника равна половине произведения его катетов
S = ½ ab
Если высоты двух треугольников
равны, то их площади относятся
как основания

СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И ВЫСОТАМИ ТРЕУГОЛЬНИКА
SABC = 1/2 a ∙ ha
SABC = 1/2 b ∙ hb
1/2 a ∙ ha = 1/2 b ∙ hb
a ∙ ha = b ∙ hb
Вывод: меньшая высота
проведена к
большему основанию

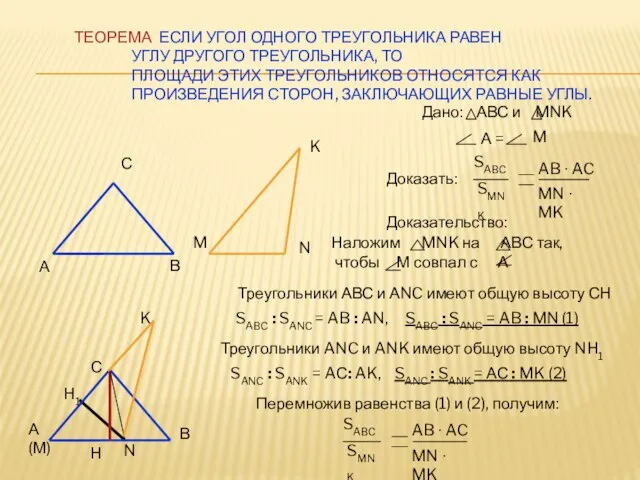
ТЕОРЕМА: ЕСЛИ УГОЛ ОДНОГО ТРЕУГОЛЬНИКА РАВЕН
УГЛУ ДРУГОГО ТРЕУГОЛЬНИКА, ТО
ПЛОЩАДИ ЭТИХ ТРЕУГОЛЬНИКОВ ОТНОСЯТСЯ КАК ПРОИЗВЕДЕНИЯ СТОРОН, ЗАКЛЮЧАЮЩИХ РАВНЫЕ УГЛЫ.
Доказательство:
Треугольники АВС и АNC имеют общую высоту СН
SABC : SANC = AB : AN, SABC : SANC = AB : MN (1)
Треугольники ANC и ANK имеют общую высоту NH1
SANC : SANK = AС: AK, SANC : SANK = АС : MK (2)

РАВНЫЕ МНОГОУГОЛЬНИКИ ИМЕЮТ РАВНЫЕ ПЛОЩАДИ

ПЛОЩАДЬ ВСЕГО МНОГОУГОЛЬНИКА РАВНА СУММЕ ПЛОЩАДЕЙ ЕГО ЧАСТЕЙ, НА КОТОРЫЕ ОН РАЗБИТ НЕКОТОРОЙ ПРЯМОЙ.

ПЛОЩАДЬ КВАДРАТА РАВНА КВАДРАТУ ДЛИНЫ ЕГО СТОРОНЫ, Т.Е. ПЛОЩАДЬ КВАДРАТА СО СТОРОНОЙ А ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ.
а
S=а2

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА:
S=а·b