«Уравнения с двумя неизвестными в целых числах »

Содержание
1.Введение.
2. Диофант и история диофантовых уравнений.
3. Теоремы о числе решений уравнений с двумя переменными.
4. Нахождение решений для некоторых частных случаев.
5. Примеры решений уравнений С6 из ЕГЭ -2010.
6. Заключение.
7. Литература.

Анализ ситуации
В этом учебном году одиннадцатиклассникам предстоит сдавать Единый государственный экзамен по математике, где КИМы составлены по новой структуре. Нет части «А», но добавлены задания в часть «В» и часть «С». Составители объясняют добавление С6 тем, что для поступления в технический ВУЗ нужно уметь решать задания такого высокого уровня сложности.

Проблема
Решая примерные варианты заданий ЕГЭ, мы заметили, что чаще всего встречаются в С6 задания на решение уравнений первой и второй степени в целых числах. Но мы не знаем способы решения таких уравнений. В связи с этим возникла необходимость изучить теорию таких уравнений и алгоритм их решения.

Цель
Уметь решать уравнения с двумя неизвестными первой и второй степени в целых числах.

Задачи
1)Изучить учебную и справочную литературу;
2)Собрать теоретический материал по способам решения уравнений;
3)Разобрать алгоритм решения уравнений данного вида;
4)Решить уравнения с двумя переменными в целых числах из материалов ЕГЭ-2010 С6.

1. Диофант и история диофантовых уравнений.
Решение уравнений в целых числах является одной из древнейших математических задач. Наибольшего расцвета эта область математики достигла в Древней Греции. Основным источником, дошедшим до нашего времени, является произведение Диофанта – «Арифметика». Диофант суммировал и расширил накопленный до него опыт решения неопределенных уравнений в целых числах.
В истории сохранилось мало фактов биографии замечательного александрийского ученого-алгебраиста Диофанта. По некоторым данным Диофант жил до 364 года н.э.

Он специализировался на решении задач в целых числах. Такие задачи в настоящее время известны под названием диофантовых.
Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения

2. Теоремы о числе решений линейного диофантового уравнения

Теорема 1
Если в уравнении ax+by=1, (a,b)=1, то уравнение имеет, по крайней мере, одно решение.

Теорема 2
Если в уравнении ax+by=c, (a,b)=d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 3
Если в уравнении ax+by=c, (a,b)=d>1 и , то оно равносильно уравнению a1x+b1y=c1, в котором (a1,b1)=1.

Теорема 4
Если в уравнении ax+by=c, (a,b)=1, то все целые решения этого уравнения заключены в формулах:
x=x0c+bt
y=y0c-at
где х0, у0 – целое решение уравнения ax+by=1, t- любое целое число.

3. Алгоритм решения уравнения в целых числах
Сформулированные теоремы позволяют составить следующий алгоритм решения в целых числах уравнения вида ax+by=c.
1. Найти наибольший общий делитель чисел a и b,
если (a,b)=d>1 и с не делится на d , то уравнение целых решений не имеет;
если (a,b)=d>1 и , то

2. Разделить почленно уравнение ax+by=c на d, получив при этом уравнение a1x+b1y=c1, в котором (a,b)=1;
3. Найти целое решение (х0, у0) уравнения a1x+b1y=1 путем представления 1 как линейной комбинации чисел a и b;
4. Составить общую формулу целых решений данного уравнения
где х0, у0 – целое решение уравнения , - любое целое число.

4 .Примеры решений уравнений первой степени двумя переменными ( С6 из ЕГЭ -2010)

Пример №1
Решить в натуральных числах уравнение:
, где т>п
Решение:
Выразим переменную п через переменную т:

Найдем делители числа 625: т-25 Є{1; 5; 25; 125; 625}
1) если т-25 =1, то т=26, п=25+625=650
2) т-25 =5, то т=30, п=150
3) т-25 =25, то т=50, п=50
4) т-25 =125, то т=150, п=30
5) т-25 =625, то т=650, п=26
Ответ: т=150, п=30
т=650, п=26

Пример №2
Решить уравнение в натуральных числах: тп +25 = 4т
Решение: тп +25 = 4т
1) выразим переменную т через п:
4т – тп =25
т(4-п) =25
т =

найдем натуральные делители числа 25: ( 4-п) Є {1; 5; 25}
если 4-п =1, то п=3, т=25
4-п =5, то п=-1, т=5 (посторонние корни)
4-п =25, то п=-21, т=1 (посторонние корни)
Ответ: (25;3)

5.Уравнения второй степени с двумя неизвестными

Пример №1
1. Решить уравнение: х2 - у2 =3 в целых числах.
Решение:
1) Применим формулу сокращенного умножения
х2 - у2=(х-у)(х+у)=3
2) Найдем делители числа 3 = {-1;-3;1;3}
3) Данное уравнение равносильно совокупности 4 систем:

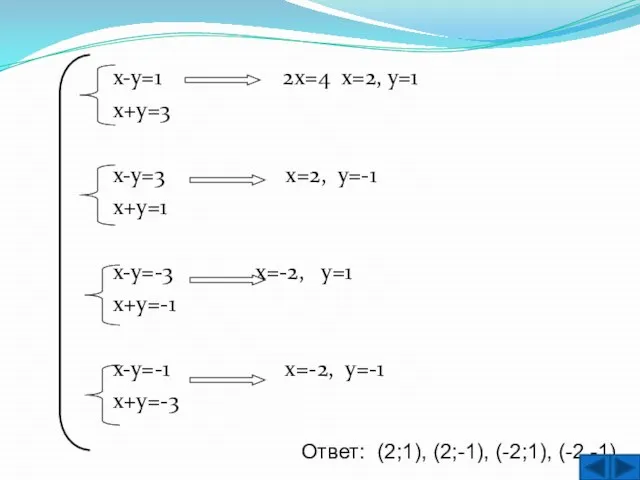
х-у=1 2х=4 х=2, у=1
х+у=3
х-у=3 х=2, у=-1
х+у=1
х-у=-3 х=-2, у=1 х+у=-1
х-у=-1 х=-2, у=-1
х+у=-3
Ответ: (2;1), (2;-1), (-2;1), (-2,-1)

2. Решить уравнение: х2+ху=10
Решение:
1) Выразим переменную у через х:
2) Дробь будет целой, если х Є {±1;±2; ±5;±10}
3) Найдем 8 значений у.
Если х=-1, то у= -9 х=-5, то у=3
x=1, то у=9 х=5, то у=-3
x=-2 ,то у=-3 х=-10, то у=9
x=2, то у=3 х=10, то у=-9

3. Решить уравнение : х3 – у3 =91
Решение: найдем делители числа 91: {±1; ±7; ±13; ±91}
Значит, уравнение равносильно совокупности 8 систем.
4.Решить уравнение в целых числах:
2х2 -2ху +9х+у=2
Решение: выразим из уравнения то неизвестное, которое входит в него только в первой степени- в данном случае у: 2х2 +9х-2=2ху-у

выделим у дроби целую часть с помощью правила деления многочлена на многочлен «углом». Получим:
Следовательно, разность 2х-1 может принимать только значения -3,-1,1,3.
Осталось перебрать эти четыре случая.
Ответ: (1;9), (2;8), (0;2), (-1;3)

5.Найдите все пары ( х; у) целых чисел, удовлетворяющие системе неравенств:
х2 +у 2< 18х – 20у - 166,
32х - у2 > х2 + 12у + 271
Решение: Выделяя полные квадраты, получим:
(х-9)2 + (у+10)2 <15
(х-16)2 + (у+6)2 <21
Из первого и второго неравенства системы :
(х-9)2 < 15 6≤ х ≤ 12
(х-16)2 < 21, 12≤ х ≤ 20 , х=12.
Подставляя х = 12 в систему, получим:
(у+10)2 < 6 -2 ≤ у+10 ≤ 2 -12 ≤ у ≤ -8
(у+6)2 < 5 -2 ≤ у+6 ≤ 2 -8 ≤ у ≤ -4 у=-8
Ответ: (12; -8)

Заключение.
Решение различного вида уравнений является одной из содержательных линий школьного курса математики, но при этом методы решения уравнений с несколькими неизвестными практически не рассматриваются. Вместе с тем, решение уравнений от нескольких неизвестных в целых числах является одной из древнейших математических задач. Большинство методов решения таких уравнений основаны на теории делимости целых чисел, интерес к которой в настоящее время определяется бурным развитием информационных технологий. В связи с этим, учащимся старших классов будет небезынтересно познакомиться с методами решения некоторых уравнений в целых числах, тем более что на олимпиадах разного уровня очень часто предлагаются задания, предполагающие решение какого-либо уравнения в целых числах, а в этом году такие уравнения включены еще и в материалы ЕГЭ.