0 0 0 1 1 0 ? 01 1 0 1 1 0 ? 1Простое высказывание – повествовательное предложение, принимающее одно из двух возможных значений – истина или

1
1
0
1
1
0
?
1

Простое высказывание –
повествовательное предложение,
принимающее одно из двух возможных значений –
истина или ложь.

Элементы алгебры логики
Высказывания.
Операции над высказываниями

А = В марте 31 день.
А = 1
В = 13 > 27.
В = 0
С = 24 – 1 – простое число.
С = 1
Закрой окно.
Который час?

Предикат –
высказывание с переменными, которое при одних значениях переменных может стать истинным высказыванием, при других – ложным.
Х>0
Город – столица России

Рассуждение –
цепочка взаимосвязанных фактов и умозаключений, вытекающих друг из друга.

Логика –
наука о доказательных рассуждениях
Аристотель
Формальная логика
Правильность рассуждения определяется только его логической конструкцией (структурой), и не зависит от
конкретного содержания входящих в него рассуждений.

Логика –
наука о доказательных рассуждениях
Джордж Буль
Математическая логика=
Формальная логика
+
алгебраические операции

Алгебра логики
(булева алгебра) -
раздел математической логики, изучающий строение логических высказываний
и способы установления их истинности с помощью алгебраических методов.

Составное высказывание – комбинация простых высказываний, соединенных логическими операциями.

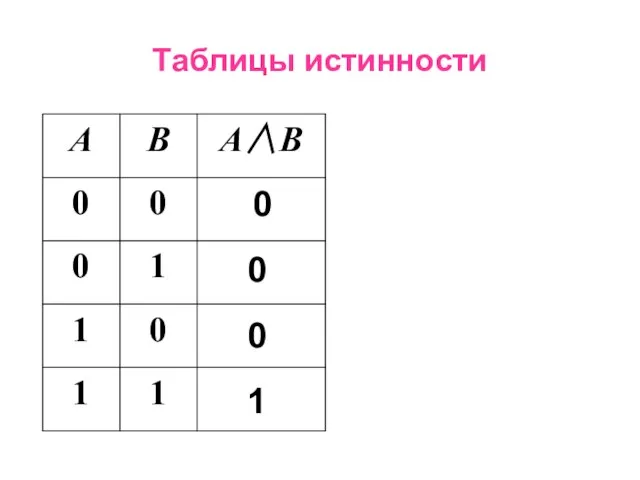
Операции над высказываниями
Логическое умножение (конъюнкция) – ∧, и, and, & -
бинарная операция, в результате которой получается составное высказывание, истинное, если истинны оба простых высказывания, и ложное, если хотя бы одно из них ложно.

Таблицы истинности
0
0
0
1

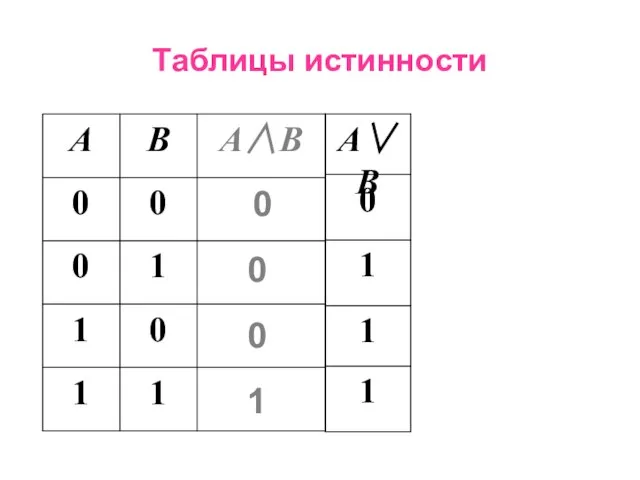
Операции над высказываниями
Логическое сложение (дизъюнкция) – ∨, или, or -
бинарная операция, в результате которой получается составное высказывание, истинное, если истинно хотя бы одно простое высказывание, и ложное, если оба ложны.

Таблицы истинности
0
0
0
1
1
1
1
0
А∨В

Операции над высказываниями
Логическое отрицание (инверсия) – А, не, not -
унарная операция, в результате которой получается составное высказывание, имеющее значение, противоположное исходному высказыванию

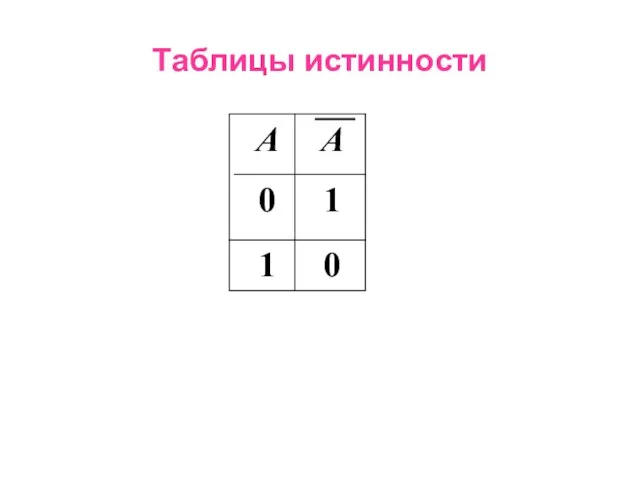
Таблицы истинности
0
1
А
1
0
А

Операции над высказываниями
Логическое следование -(импликация) – → ⇒, следовательно, если …, то … -
бинарная операция, в результате которой получается составное высказывание, ложное тогда и только тогда, когда из истины следует ложь.

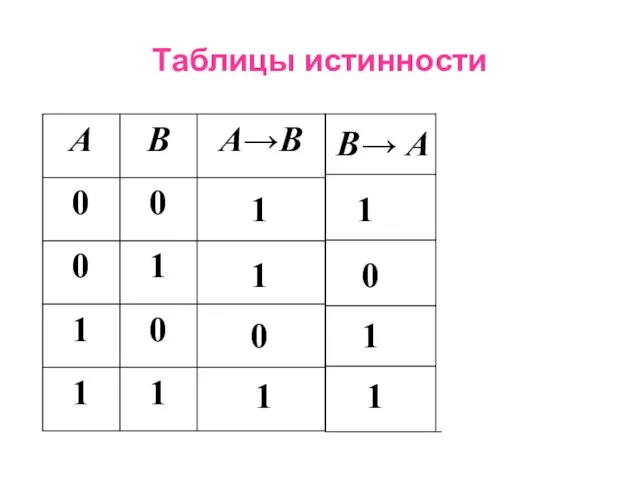
Таблицы истинности
1
1
0
1
1
0
1
1

Операции над высказываниями
Равнозначность - (эквиваленция) – ↔ … тогда и только тогда, когда …
бинарная операция, в результате которой получается составное высказывание, истинное при одинаковых значениях простых высказываний, и ложное при разных значениях.

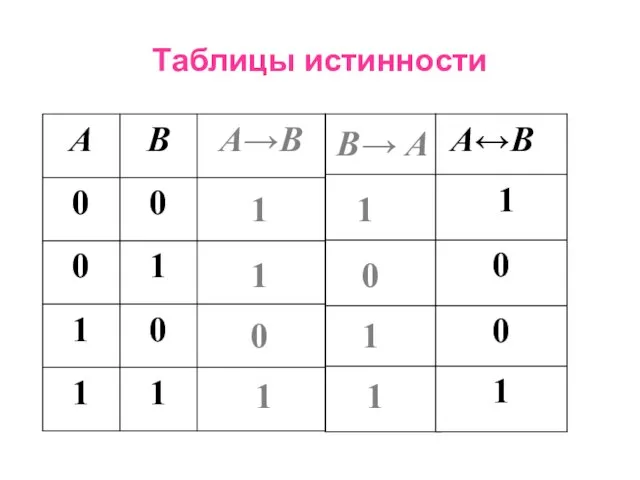
Таблицы истинности
1
1
0
1
1
0
1
1
1
0
0
1
А↔В

Операции над высказываниями
Исключащее ИЛИ ⊕, xor либо …, либо….
бинарная операция, в результате которой получается составное высказывание, истинное при разных значениях простых высказываний, и ложное при одинаковых значениях.

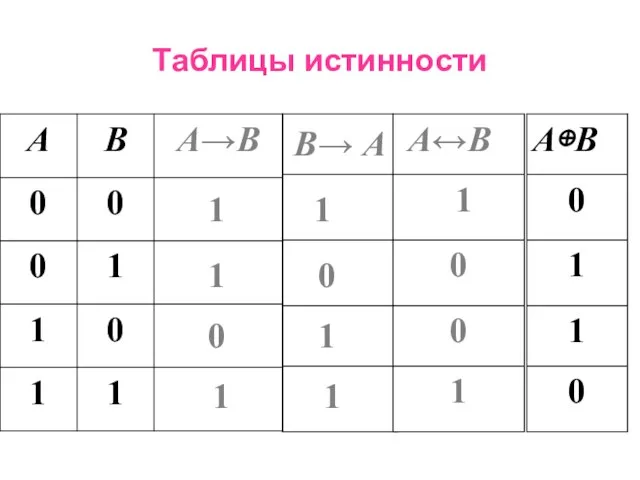
Таблицы истинности
0
1
1
0
А⊕В

Приоритетность логических операций
Скобки
Инверсия
Конъюнкция
Дизъюнкция, исключающее ИЛИ
Импликация
Эквиваленция