212685

План
Понятие задачи. Основные компоненты задачи
Роль задач в обучении математике
Типология задач
Этапы решения задачи
Методические основы обучения учащихся решению задач
Организационные формы обучения решению задач

Трактовки понятия «задача»
(по исследованиям Г.А. Балла)
Термин «задача» употребляется по отношению к объектам, относящимся к трем категориям:
цель действия субъекта, требования поставленные перед субъектом (А.Н.Леонтьев);
ситуация, включающая не только цель, но и условия, в которых цель должна быть достигнута (Ю.М. Колягин, П.М. Эрдниев);
словесная формулировка, описывающая ситуацию (Л.М. Фридман).

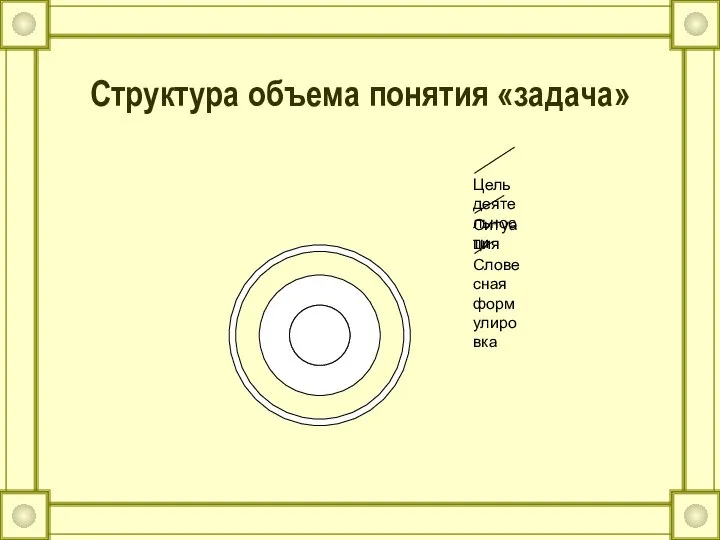
Структура объема понятия «задача»

Основные компоненты задачи
условие - начальное состояние;
базис решения – теоретическое обоснование решения;
решение – преобразование условия для нахождения требуемого заключением искомого;
заключение – конечное состояние.

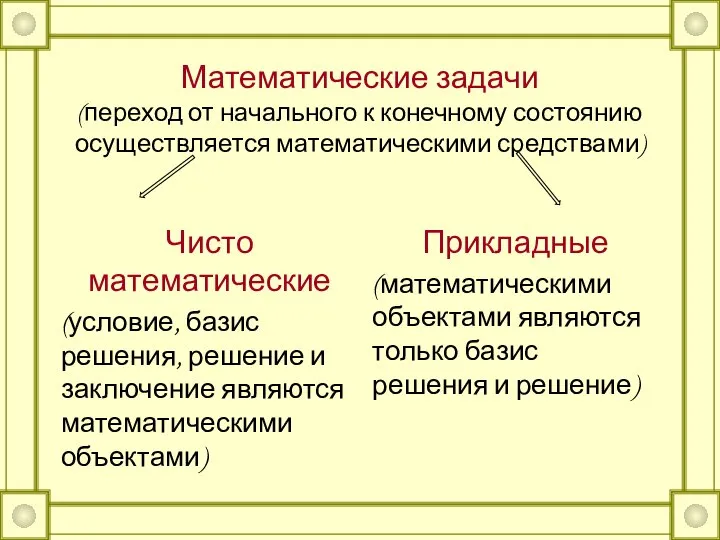
Математические задачи
(переход от начального к конечному состоянию осуществляется математическими средствами)
Чисто математические
(условие, базис решения, решение и заключение являются математическими объектами)
Прикладные
(математическими объектами являются только базис решения и решение)

Этапы истории использования задач
в обучении математике
I. Изучение математики с целью обучения решению задач.
II. Обучение математике, сопровождаемое решением задач.
III. Обучение математике через решение задач.

Двуединая роль задач в обучении математике:
задачи выступают и как цель, и как средство обучения математике
Место и функции задач в обучении математике определяются в зависимости от целей обучения и могут иметь образовательное, воспитательное и практическое значение

Учебные цели решения задач
формирование мотивации и интереса учащихся к математической деятельности;
иллюстрация и конкретизация изученного учебного материала;
выработка специальных умений и навыков;
контроль и оценка знаний, умений учащихся и результатов их деятельности.

Функции решения математических задач
Функция задачи - проектируемое учителем изменение в деятельности и психике учащихся
В педагогической практике выделяют:
дидактические функции;
познавательные функции;
развивающие функции

Функции задач как цели обучения
Усвоение:
понятия задачи, ее структуры и компонентов;
сущности процесса решения;
приемов работы с текстом задачи;
способов решения отдельных видов задач;
общих методов поиска решения.

Функции задач как средства обучения
обучение математической деятельности;
формирование знаний, умений, навыков;
обучение моделированию явлений действительности;
развитие учащихся (качеств мышления);
воспитание через организацию деятельности, общение.

Следует иметь в виду следующие обстоятельства:
Большинство математических задач полифункционально, т.е. одна и та же задача может выполнять одновременно различные функции, т.к. в результате решения может происходить не одно, а несколько изменений.
Среди всех функций всегда можно выделить главную, ради которой решается задача.
Любая типология или классификация является условной.
Любая математическая задача обладает признаками различных классификационных схем.

Классификации задач
По функциональному назначению:
с дидактическими функциями;
с познавательными функциями;
с развивающими функциями.
По компонентам учебной деятельности:
организационно-действенные;
стимулирующие;
контрольно-оценочные.
По связи между компонентами:
алгоритмические;
полуалгоритмические;
эвристические.

Классификации задач
По величине проблемности:
стандартные (все компоненты известны);
обучающие (один из компонентов неизвестен);
поисковые (два компонента неизвестны);
проблемные (три компонента неизвестны).
По отношению между условиями и требованием:
определенные;
недоопределенные;
переопределенные.

Классификации задач
По числу объектов в условии задачи:
простые;
составные.
По характеру требований:
на доказательство;
на вычисления;
на построение;
на исследование и др.
По специфике языка:
текстовые;
сюжетные;
абстрактные (предметные).

Классификации задач
По принадлежности к определенному разделу математики:
арифметические;
алгебраические;
геометрические;
тригонометрические;
комбинаторные и др.

Примеры задач различных типов
Алгоритмическая задача – задача, решаемая с помощью непосредственного применения определения, правила или теоремы
Например:
найти гипотенузу треугольника, если известны его катеты.
Полуалгоритмическая задача – задача, решаемая с помощью правил, имеющих обобщенный характер и не сводящихся к выполнению определенной последовательности элементарных актов, но при этом связи между элементами задачи легко обнаруживаются и каждая из подзадач является алгоритмической
Например:
Найти периметр равнобедренного треугольника по боковой стороне и высоте, проведенной к основанию.

Примеры задач различных типов
Эвристическая задача – задача со скрытыми связями между элементами или способом решения, не являющимся конкретизацией обобщенного правила.
Например:
Найти расстояние от середины высоты треугольника, проведенной к меньшей из его сторон, до большей стороны, если длины всех сторон треугольника известны.
Стандартная задача – четко определено условие, известен способ ее решения, его обоснование , а также известен способ воспроизведения известного.
Например:
Зная два угла треугольника, вычислить третий;
Решить квадратное уравнение общего вида: х2 – 5х +6 = 0

Примеры задач различных типов
Обучающая задача – задача, в которой не известен или плохо определен один из компонентов
Например:
Придумайте квадратное уравнение, корнями которого являются числа 2 и -2, если известно, что для решения уравнения использовалась формула разности квадратов.
Поисковая задача – задача, в которой неизвестны или плохо определяются два компонента
Например:
Решите уравнение: (х2 +5х +6) 2 + 5(х +1) + х2 +1 = 0
Проблемная задача – задача, в которой неизвестны три компонента.
Например (до изучения квадратных уравнений):
Составьте текст сюжетной задачи, для решения которой можно составить уравнение

Примеры задач различных типов
Определенные задачи – задачи, в которых задано необходимое и достаточное число элементарных условий для удовлетворения требованиям.
Недоопределенные задачи – задачи, в которых недостаточно условий для ее решения
Например:
С двух цветков, расстояние между которыми 200м, в разных направлениях вылетели две стрекозы с одинаковой скоростью 25 м в минуту. Какое расстояние между ними будет через 2 минуты?
Переопределенные задачи – задачи, имеющие для решения лишние условия, которые могут быть либо следствием других, либо противоречить другим
Например:
Найдите радиус окружности, описанной вокруг прямоугольного треугольника со сторонами 5см, 12 см и 13 см.
Длины сторон прямоугольного треугольника равны 3см, 4сми 6 см. Определите величину угла, лежащего против меньшего из катетов.

Сложность и трудность задачи
Сложность – объективная характеристика задачи, зависящая от числа объектов задачи, от количества и характера связей между объектами, конструкции текста, языка, на котором приведена формулировка и т.п.
Трудность – субъективная характеристика задачи, зависящая от знаний, умений и опыта решающего задачу субъекта, от уровня его интеллектуальных умений, связанных с типологическими свойствами личности, от жизненного опыта и т.п.

Трактовки термина «решение задачи»
Решение задачи – план (способ, метод) осуществления требования задачи;
Решение задачи – процесс выполнения плана, приводящего к осуществлению требования задачи;
Решение задачи – результат выполнения плана осуществления требования задачи.

Структура процесса решения задачи
(по Л.М. Фридману)
Содержательный и логический анализ.
Схематическая запись условия (построение высказывательной модели задачи с использованием схем, чертежей, графиков, математической символики и т.п.).
Поиск способа (плана) решения, нахождение его теоретической базы.
Осуществление способа (плана) решения.
Проверка найденного решения.
Исследование задачи и найденного решения.
Формулировка ответа.
Учебно-познавательный анализ задачи и ее решения.

«Если хотите научиться решать задачи, то решайте их!» (Д. Пойа)
На решение задач по математике затрачивается около половины всего учебного времени.
Количество задач, решенных учащимися за 10 лет обучения, исчисляется несколькими десятками тысяч.
Чем старше учащиеся, тем чаще при решении малознакомой задачи они произносят печально-известные слова « …»

Итоги PISA
российских школьников
По математической грамотности
2000 год
среди 32 стран участниц 21-25 места,
2003 год
среди 40 стран участниц 29-31 места.
2006 год
?

Причины несформированности
умения решать задачи
Психологическая причина: основным мотивом решения задач являются внешние мотивы благополучия в виде отметки, престижа, поощрения и т.п., в то время как для успешного обучения решению задач основным мотивом должно быть желание «научиться решать задачи».
Методическая причина: для овладения такой сложной деятельностью, как решение задач, должна быть сформирована ориентировочная основа этой деятельности. А именно ее и нет при обучении математики в традиционной методике.

Структура ориентировочной основы умения решать задачи
ясное представление о сущности и основных объектах задачи;
владение элементарными действиями и операциями, из которых состоит деятельность решения математических задач;
знание основных методов решения задач и умение ими пользоваться.

I блок ориентировочной основы решения задач -
минимум знаний о сущности задач и их решений
Представление об источниках возникновения (генезисе) задач:
проблемная ситуация – основной источник возникновения задачи;
задача – знаковая модель проблемной ситуации;
в отличии от реальных ситуация в задачах можно абстрагироваться от некоторых свойств субъектов или объектов, поэтому задачи можно придумывать и переделывать.

I блок ориентировочной основы решения задач -
минимум знаний о сущности задач и их решений
Знание о структуре задачи:
в каждой задаче рассматривается один или несколько объектов;
относительно каждого объекта указываются количественные или качественные характеристики в виде высказываний, принимаемых за истинные;
высказывания или высказывательные формы о свойствах объекта составляют условие задачи;
задача обязательно имеет вопрос или требование.

I блок ориентировочной основы решения задач -
минимум знаний о сущности задач и их решений
Умение развертывать условие и заключение в систему взаимосвязанных высказываний:
текст задачи дается, как правило, в свернутом виде;
для разворачивания условия или заключения удобно вводит обозначения, схемы, таблицы, чертежи, и т.п.;
очень часто следует рассматривать неявно заданные, но предполагаемые условия.

I блок ориентировочной основы решения задач -
минимум знаний о сущности задач и их решений
Понимание сущности процесса решения задачи:
решить математическую задачу – это значит найти такую последовательность общих положений теории, применение которой к условию задачи или промежуточным результатам (т.е. к следствиям условий) дает то, что требуется в задаче;
последовательность положений теории образует базу (обоснование) решения;
решение задачи состоит из определенных этапов, каждый из которых имеет важное значение для овладения умением решать задачи.

II блок ориентировочной основы решения задач -
основные действия и операции, входящие в состав умения решать задачи
Владение умениями
расчленять текста задачи на элементарные условия и требования;
устанавливать объекты задачи и их характеристики;
определять характер объектов и связи между ними как явные, так и неявные;
составлять репрезентативные модели задачи (схемы, чертежи, таблицы и т.п.);
составлять решающие модели задачи (вычислительные формулы, уравнения или их системы);
анализировать полученные решения;
формулировать ответ.

III блок ориентировочной основы решения задач -
общие методы решения задач
Общая идея, лежащая в основе всех методов и способов решения задач: чтобы решить новую задачу, нужно свести ее к одной или нескольким ранее решенным задачам
Способ решения – совокупность действий для решения конкретной задачи
Метод решения – общая схема, на которой строятся способы решения

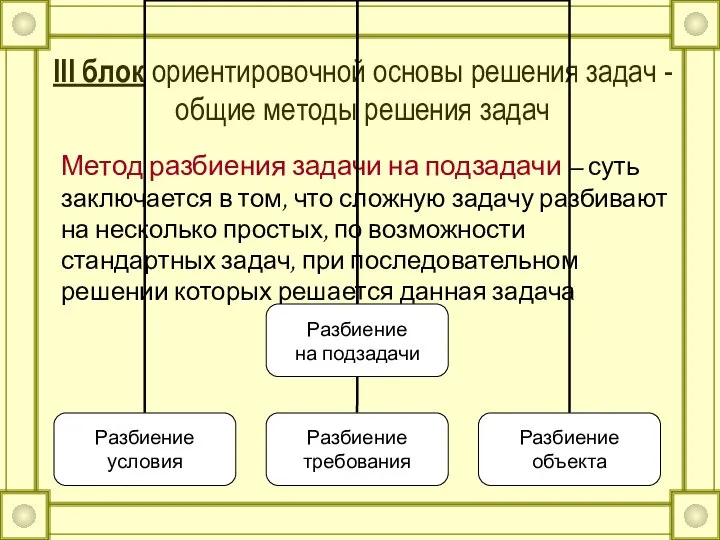
III блок ориентировочной основы решения задач -
общие методы решения задач
Метод разбиения задачи на подзадачи – суть заключается в том, что сложную задачу разбивают на несколько простых, по возможности стандартных задач, при последовательном решении которых решается данная задача

III блок ориентировочной основы решения задач -
общие методы решения задач
Следует иметь в виду, что
Для решения многих задач применяется не один, а сразу несколько общих методов.
Для решения многих задач имеется не один, а несколько способов.
Способ решения зависит от применяемых общих методов и последовательности их применения.
Существуют и некоторые менее общие методы или приемы (например, метод оценок или метод исчерпывающих проб).

III блок ориентировочной основы решения задач -
общие методы решения задач
Метод преобразования задачи – суть заключается в том, что с помощью какого-либо приема задача преобразуется в более простую, понятную или известную, но в эквивалентную задачу

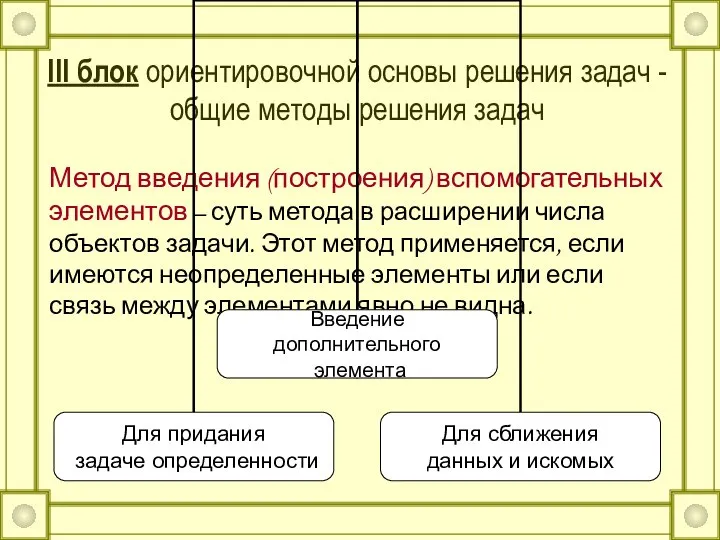
III блок ориентировочной основы решения задач -
общие методы решения задач
Метод введения (построения) вспомогательных элементов – суть метода в расширении числа объектов задачи. Этот метод применяется, если имеются неопределенные элементы или если связь между элементами явно не видна.

Умение решать задачи,
с позиций современных требований
к процессу обучения,
должно рассматриваться как
результат синтеза
знаний и умений
Вывод:

Преодоление стихийности формирования ориентировочной основы решения задач, создание прочной ориентировочной основы для решения задач
Смещение акцента с дидактической на познавательную функцию обучения решению задач
Формирование у учащихся не только частных умений решения типовых задач, но и формирование и развитие у них общих умений решения любых математических (в том числе и прикладных) задач
Дифференциация процесса обучения решению задач.
Основные направления совершенствования методики обучения учащихся решению задач

Формы организации обучения решению задач
Фронтальное решение:
фронтальное устное решение задач по готовым записям или чертежам;
фронтальное решение задачи с записью хода решения на доске учителем или отдельными учениками;
самостоятельное решение с последующей фронтальной проверкой решений.
Индивидуальное решение:
самостоятельное выполнение общих заданий с оказанием дифференцированной помощи;
самостоятельное решение дифференцированных заданий с последующим обсуждением способов решения;
домашнее решение задач;
индивидуальное решение для устранения пробелов.

Особенности решения учебной математической задачи
Учебно-познавательный анализ –
важнейший этап решения учебной задачи, включающий:
обсуждение действий поиска решения (как возникла идея решения? Что помогло найти решение?);
выявление связей с ранее решенными задачами;
поиск и осуществление других способов решения, их сравнение и выбор оптимального с точки зрения затрат решения;
фиксация поучительных выводов из проделанной работы (в каких случаях можно использовать найденный способ или прием решения).