Алгебра логики

Романов Константин Михайлович, учитель информатики
История появления логики
Построение и анализ логических элементов и схем ЭВМ основываются на применение формального метода математики к области логики
Основоположником математической логики считают великого немецкого математика Лейбница. Это он, в XVII веке попытался построить первые логические исчисления. Он сблизил логику с исчислением, усовершенствовал и уточнил логическую символику.
На фундаменте, заложенном Лейбницем, другой великий математик Джордж Буль продолжал изучать логику.

Романов Константин Михайлович, учитель информатики
Джордж Буль
В ХIXв. в трудах английского математика Дж. Буля начала формироваться новая область математических знаний - алгебра логики, созданная для решения традиционных логических задач алгебраическими методами. Он вывел для логических построений особую алгебру - алгебру логики. В ней, в отличие от обычной алгебры, символами обозначают не числа, а высказывания.

Романов Константин Михайлович, учитель информатики
Основные формы
Слово логика означает как совокупность правил, которым подчиняется процесс мышления, так и науку о правилах рассуждений. Логика, как наука о законах и формах мышления изучает абстрактное мышление как средство познания объективного мира.
Основными формами абстрактного мышления являются:
понятие
суждение
умозаключение

Романов Константин Михайлович, учитель информатики
Логические элементы в ЭВМ
В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы математической логики. Знание логики необходимо:
при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции;
при решении задач (составлении отчетов) с условиями в электронных таблицах;
для построения фильтров для запросов в базах данных;
для поиска информации в Интернете.

Романов Константин Михайлович, учитель информатики
К основным понятиям логики
относятся следующие:
Высказывание (суждение) - некоторое предложение, которое может быть истинно (верно) или ложно. Например, высказывание «Сумма внутренних углов треугольника равна 180°» - истинно, а высказывание «Все углы треугольника - прямые» - ложно.
Истинность или ложность получаемых таким образом высказываний и соответствующей трактовки связок как операций над высказываниями.
Для обозначения истинности водится символ И (или 1), а для обозначения ложности - Л (или 0).

Романов Константин Михайлович, учитель информатики
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Является ли высказыванием ?
Птицы летят на север.
Информатика- интересный предмет.
Сколько сейчас времени?
Сейчас идет снег.
Логические высказывания

Романов Константин Михайлович, учитель информатики
Основные понятия логики
Конъюнкцией высказываний (логическим умножением) называется логическая операция, которая принимает значение истинна тогда и только тогда, когда истинны исходные логические выражения. Обозначается (X∧У), читается «X и У».
Дизъюнкцией высказываний (логическим сложением) называется логическая операция, которая принимает значение истина тогда и только тогда, когда истинно хотя бы одно из исходных логических выражений. Обозначается (X∨У), читается «X или У».

Романов Константин Михайлович, учитель информатики
Основные понятия логики
Отрицание или инверсия, определяется следующим образом если выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то его отрицание будет истинным. Обозначается (¬X), читается «не X».
Импликацией высказываний (логическое следование) называется логическая операция, которая принимает значение ложь тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Обозначается (X ⇒ У), читается «Если X, то У».

Романов Константин Михайлович, учитель информатики
Основные понятия логики
Эквивалентностью высказываний называется логическая операция, которая принимает значение истинно тогда и только тогда, когда исходные выражения одновременно истинны или одновременно ложны. Обозначается (X ⇔ У) , читается «X эквивалентно У».
Употребляемые в обычной речи логические связки «и», «или», «если ..., то», «эквивалентно», частица «не» позволяют из уже заданных высказываний строить новые, более «сложные высказывания. Так, из высказываний «Х > 2», «Х ≤ 3» при помощи связки «и» можно получить «Х > 2 и Х ≤ 3», при помощи связки «или» - «Х > 2 или Х ≤ 3».

Романов Константин Михайлович, учитель информатики
Все задачи раздела «Основы логики и логические основы компьютера» можно разделить на группы:
на пересечение и объединение множеств;
построение таблиц истинности выражений;
упрощение логических формул;
написание структурных формул для переключательных схем;
написание логических формул по комбинационной схеме устройства;
текстовые задачи.

Романов Константин Михайлович, учитель информатики
При решении задач по логике необходимо помнить:

Романов Константин Михайлович, учитель информатики
Таблицы истинности
Для задания функций алгебры логики иногда используют таблицы, содержащие все наборы значений переменных и значения функций на этих наборах. Это так называемый табличный способ задания функций.
Сами же таблицы в алгебре логике называют таблицами истинности (истинностные таблицы).
Так например: таблица, задающая логическое отрицание ¬X, умножение (конъюнкция) X∧У , сложение (дизъюнкция ) X∨У, следования (импликация) X⇒У, эквивалентность X⇔У, имеет следующий вид:

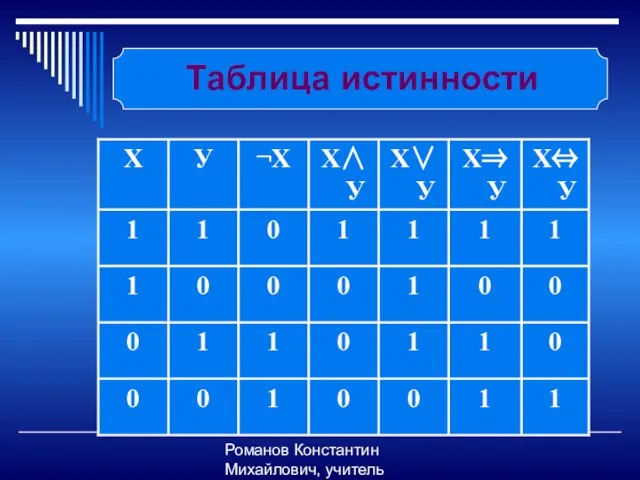
Романов Константин Михайлович, учитель информатики
Таблица истинности

Романов Константин Михайлович, учитель информатики
Законы алгебры логики

Романов Константин Михайлович, учитель информатики
Законы алгебры логики

Романов Константин Михайлович, учитель информатики
Записать в виде логического выражения следующее высказывание: «Зимой Саша поедет в деревню и, если будет хорошая погода, то он будет кататься на лыжах»
Проанализируем составное высказывание.
Оно состоит из следующих простых высказываний: «Саша поедет в деревню», «Будет хорошая погода», «он будет кататься на лыжах». Обозначим их через логические переменные:
А= Саша поедет в деревню;
В= Будет хорошая погода;
С=Он будет кататься на лыжах;
Запишем высказывание в виде логического выражения, учитывая порядок действий. Если необходимо расставим скобки:
F=A&(B C)
Пример 1

Романов Константин Михайлович, учитель информатики
Запишите следующие высказывания в виде логических выражений:
Число 19 нечетное и двузначное.
Если Катя- сестра Миша, то Миша- брат Кати.
Если число делится на 4 , то оно- четное. Не переходи улицу на красный свет.
Неверно, что кролик- хищное животное.
Упражнение 1

Романов Константин Михайлович, учитель информатики
Запишите логические выражения, соответствующие следующим высказываниям:
Ботаника изучает растения и ботаника изучает животных.
В состав атома входят электроны или в состав электронов входят атомы.
Гелий- это жидкость и вода- это газ.
Неверно, что положительный ион- это лишившийся электронов атом.
Упражнение 2

Романов Константин Михайлович, учитель информатики
Запишите следующие высказывания в виде логических выражений:
Если будет светить солнце, то ребята пойдут в зоопарк, а если пойдет дождь, то ребята займутся уборкой квартиры.
Мы поедем в деревню и, если встретим там друзей, то интересно проведем время.
Неверно, что если солнце светит, то ветер дует только тогда, когда идет дождь.
Упражнение 3

Романов Константин Михайлович, учитель информатики
Какое из суждений ложно:
1) В пятеричной системе счисления
2 + 3 = 10
2) 1 байт = 8 бит
3) Некоторые простые числа, большие 101 , делятся на 3
4) В семеричной системе счисления 10 - нечетное число

Романов Константин Михайлович, учитель информатики
. Закон нарушили двое из 4-х граждан: А, В, С, D. Напишите в алфавитном порядке без запятой кто это, если известно что:
1) Если нарушил А или не нарушил В, то нарушил С и не нарушил D
2) Если не нарушил D или нарушил С, то не нарушил А и не нарушил В
Задача