Слайд 2История судоку
Прообразом судоку -“Магический квадрат”, появился в Китае 2000 лет назад.
Квадрат

размером 3х3 клетки. В каждую клетку число от 1 до 9. Сумма чисел в любом столбце, строке и по диагонали равнялась 15.
Леонард Эйлер(1707-1783). Магические квадраты для 9, 16, 25 и 36 ячеек.
1979г. Word Games magazine. Гарвард Гаррис.
Su – число, duko – единственное.
12 ноября 2004г. The Times.
Слайд 3 Правила и цель игры
Квадрат 9х9. Цифры от 1 до 9. В
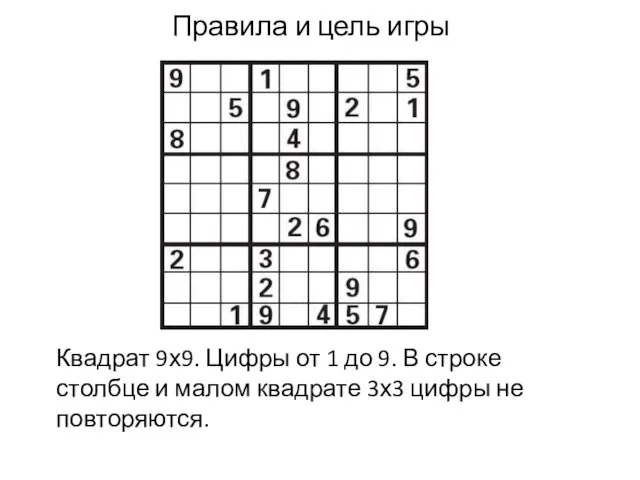
строке столбце и малом квадрате 3х3 цифры не повторяются.
Слайд 4Правила и цель игры
Несколько уровней сложности(сложность зависит не только от количества заполненных

клеток, а и от положения).
Разные по размеру(4х4, 9х9,16х16 и так далее. В журналах встречаются нестандартного размера, пр. 9х12).
Приёмы решения одинаковы(не зависят от размера и сложности, так что один и тот же алгоритм подойдёт как для 9х9, так и для 16х16).
Слайд 5Способы решения судоку
Как задачи CSP
Множество переменных, Х1,Х2,…,Хn и множеством ограничений, C1,C2,…,Cm. Каждая

Xi имеет непустую область определения Di (числа от 1 до 9) возможных значений.
Каждое Ci включает некоторое подмножество переменных и задаёт допустимые комбинации значений для этого подмножества. Состояние задачи - присваивание значений некоторым переменным.
Присваивание, которое не нарушает никаких ограничений, называется совместимым, или допустимым присваиванием.
Полным называется такое присваивание, в котором учавствует каждая переменная, а решением CSP задачи является полное присваивание, которое удовлетворяет всем ограничениям.
Слайд 6Способы решения судоку
Любой задаче CSP может быть дана инкрементная формулировка, как и

любой стандартной задаче поиска:
Начальное состояние. Изначально в некоторых клетках вписаны числа, то есть переменные, соответствующие этим клеткам, инициализированы некоторыми значениями, не нарушающими ограничения.
Функция определения преемника. Значение может быть присвоено любой переменной с неприсвоенным значением, при условии, что переменная не будет конфликтовать с другими переменными, значения которым были присвоены ранее.
Проверка цели. Проверка того, что текущее присваивание является полным, то есть заполнены все 81 клетки и не нарушается ни одно из ограничений.
Слайд 7Способы решения судоку
Методы решения таких задач:
Поиск в ширину (n!*dn ветвей дерева)
Поиск в

глубину
Поиск в глубину может быть усовершенствован:
Эвристики(Minimum Remaining Values - MRV)
Предварительная проверка(распространение ограничений)
Хронологический поиск с возвратами(при неудаче возврат к предыдущей переменной, либо к переменной из конфликтного множества. Его определяет предварительная проверка)
Слайд 8Приёмы решения судоку
Приёмы, упрощающие дерево поиска
Одиночки
Скрытые одиночки
Запертый кандидат
Открытые пары(тройки, четвёрки)
Скрытые пары(тройки, четвёрки)
X-wing
Одиночки.

Метод заключается в отыскании в таблице одиночек, т.е. ячеек, в которых возможна только одна цифра и никакая другая. Вписываем её и исключаем её из других клеток этой строки, таблицы и блока.
Слайд 9 Приёмы решения судоку
Скрытые одиночки. 4 в зелёном блоке только в одной
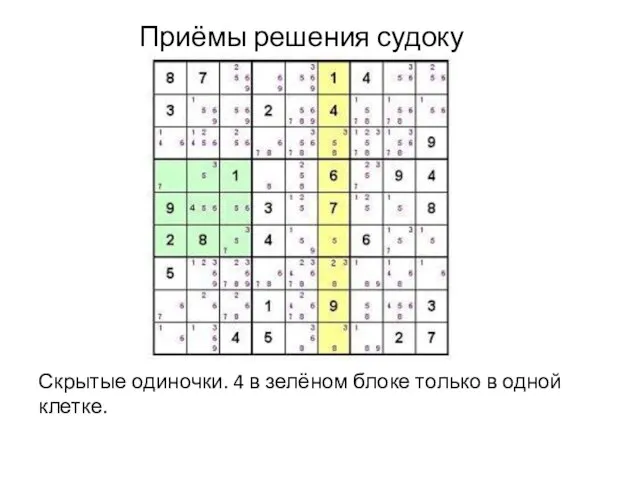
клетке.
Слайд 10 Приёмы решения судоку
Запертый кандидат. В пределах блока цифра только в одной
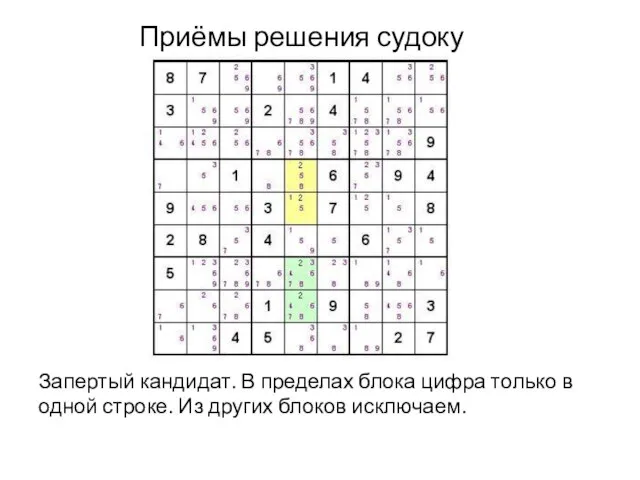
строке. Из других блоков исключаем.
Слайд 11 Приёмы решения судоку
Открытые пары. Если две ячейки в группе (строке, столбце,

блоке) содержат идентичную пару кандидатов и ничего более, то никакие другие ячейки этой группы не могут иметь значения этой пары.
Слайд 12 Приёмы решения судоку
Скрытые пары. Если в двух ячейках в группе (строке,

столбце, блоке) содержат кандидаты, среди которых идентичная пара, не встречающаяся ни в одной другой ячейке данного блока, то никакие другие ячейки этой группы не могут иметь значения этой пары.
Слайд 13 Приёмы решения судоку
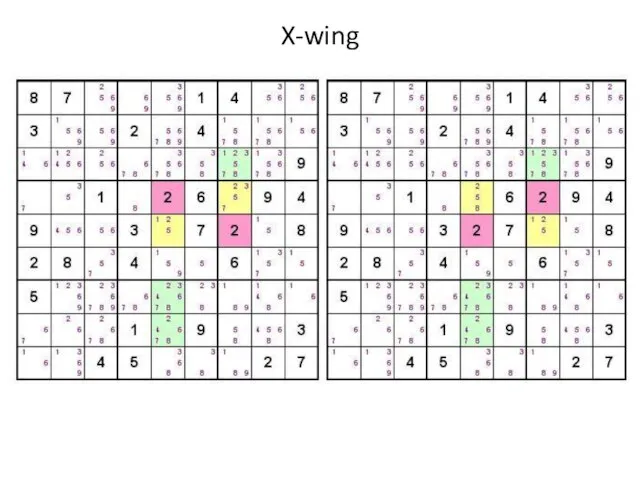
X-wing. Если значение имеет только два возможных местоположения в

какой-то строке (столбце), то оно обязательно должно быть назначено в одну из этих ячеек. Если же существует еще одна строка (столбец), где этот же кандидат также может быть только в двух ячейках и столбцы (строки) этих ячеек совпадают, то ни одна другая ячейка этих столбцов (строк) не может содержать данную цифру.
Слайд 15Реализация программы
Среда разработки – Delphi 7.
3 режима :
Решение вводимого судоку программой
Решение судоку,

сгенерированного программой, пользователем
Генерация судоку, определённого уровня сложности
Работает с судоку общего вида, однако тестировалась в основном для 9х9.
Слайд 16Реализация программы
Решение вводимого судоку программой.
Программа генерирует пустой квадрат с количеством ячеек, определяемым

пользователем.
Пользователь может кликнуть на любую из ячеек и вписать туда цифру, нажатием соответствующей клавиши на клавиатуре.
После введения некоторого количества чисел, пользователь может кликнуть по кнопке “Решить” и программа предоставит ему возможный вариант решения, либо сообщит о том, решение данного судоку не существует.
Слайд 17Реализация программы
Введеный судоку программа решает с помощью
Простой перебор с возвратами с эвристикой

типа MRV (то есть вначале заполняются такие клетки, в которые можно подставить наименьшее количество цифр)
Второй алгоритм представляет собой тот же поиск с возвратами, однако в нём программа пытается найти ситуации, описанные ранее в “приёмах решения судоку”.
Программа выдаёт количество присваиваний, которое сделала в процессе решения, таким образом предоставляя возможность сравнить эффективность второго алгоритма, по сравнению с первым.
Так же программа может выдавать количество возможных решений введённого судоку.
Слайд 18Реализация программы
Решение судоку, сгенерированного программой, пользователем.
После выбора уровня сложности и количества ячеек,

программа создаёт квадрат N x N, некоторые числа которого заполнены цифрами.
Пользователь, кликая по ячейкам и нажимая на цифры на клавиатуре, заполняет данный квадрат до того момента, пока остаются пустые клетки.
В случае введения ошибочной цифры, пользователь может выбрать эту же клетку и поставить в неё другую цифру.
Слайд 19Реализация программы
Режим контроля ввода. При включении этой опции, программа будет выдавать ошибку

в случаях, когда введённая пользователем цифра недопустима из-за того, что по горизонтали, вертикали или в блоке 3х3 такая цифра уже имеется.
Режим подсказок. В случаях, когда пользователь затрудняется в выборе того, какую цифру и в какую клетку поставить, он может включить режим подсказок. В этом режиме, программа будет выдавать для каждой клетки перечень цифр, которые возможно поставить в эту клетку, без нарушения правил игры.
Слайд 20Реализация программы
Генерация судоку выбранного уровня сложности.
Модификация готового судоку.
Генерация ответа с последующим вычёркиванием

некоторых цифр с проверкой единственности решения на каждом этапе.
Заполнение пустого квадрата цифрами, с проверкой существования и единственности решения.
Слайд 21Итоги и цели
Генерация судоку выбранного уровня сложности
Тестирование работы алгоритмов решения для судоку

произвольного размера
Поиск новых приёмов решения судоку
Задача судоку, имеющего единственное решение при минимальном количестве цифр.
http://units.maths.uwa.edu.au/~gordon/sudokumin.php



















 Художник в театре
Художник в театре Кукла Карельская рванка
Кукла Карельская рванка Языки народов мира
Языки народов мира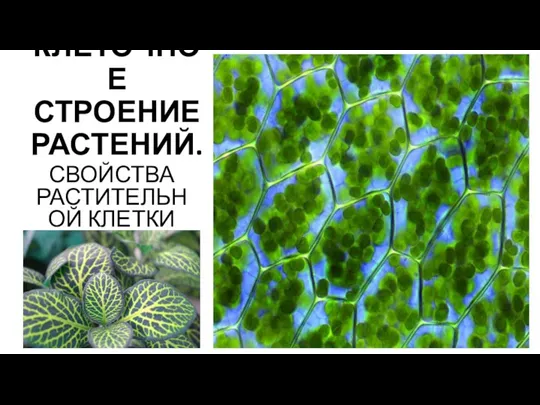 РАСТИТЕЛЬНАЯ КЛЕТКА
РАСТИТЕЛЬНАЯ КЛЕТКА Презентация на тему День Ивана Купалы
Презентация на тему День Ивана Купалы  Действия туристской группы в ЧС по организации поиска туриста, отставшего от группы
Действия туристской группы в ЧС по организации поиска туриста, отставшего от группы Услуги АО Федеральная корпорация по развитию малого и среднего предпринимательства
Услуги АО Федеральная корпорация по развитию малого и среднего предпринимательства Troubleshooting guide (h/s)
Troubleshooting guide (h/s) FCG Academy: Подготовка к экзамену по международному стандарту финансовой отчетности АССА ДипИФР
FCG Academy: Подготовка к экзамену по международному стандарту финансовой отчетности АССА ДипИФР Сравнительный анализ пространственных структур белков
Сравнительный анализ пространственных структур белков Типовые условия работы. Внедрение и сопровождение 1С в Тосно и Тосненском районе
Типовые условия работы. Внедрение и сопровождение 1С в Тосно и Тосненском районе Обеспечение взаимосвязи фундаментальных и специальных дисциплин в учебном процессе Вуза И.Е. Денежкина, А.Б. Шаповал ФИНАНСОВЫЙ У
Обеспечение взаимосвязи фундаментальных и специальных дисциплин в учебном процессе Вуза И.Е. Денежкина, А.Б. Шаповал ФИНАНСОВЫЙ У История Советского и Российского оружия
История Советского и Российского оружия Марафон похудения Гузель Уразовой
Марафон похудения Гузель Уразовой Презентация на тему Анализ рассказа Ю.П. Казакова «Тихое утро»
Презентация на тему Анализ рассказа Ю.П. Казакова «Тихое утро» Подготовка и оснащение аудитории для проведения ОГЭ по химии, комплектование лабораторного оборудования
Подготовка и оснащение аудитории для проведения ОГЭ по химии, комплектование лабораторного оборудования Измерение времени (2 класс)
Измерение времени (2 класс) Типы текстовых редакторов
Типы текстовых редакторов Презентация на тему Испания
Презентация на тему Испания Шары из фольги
Шары из фольги Физика в детских игрушках
Физика в детских игрушках Осуществление и защита частных прав
Осуществление и защита частных прав Виды игровых средств для сенсорного развития
Виды игровых средств для сенсорного развития 14 жовтня
14 жовтня Влияние рекламных роликов на формирование выбора избирателей
Влияние рекламных роликов на формирование выбора избирателей Атомные технологии
Атомные технологии Международные отношения и внешняя политика СССР в 1930 гг
Международные отношения и внешняя политика СССР в 1930 гг ЛИЧНОСТНОЕ РАЗВИТИЕ ОБУЧАЮЩИХСЯ В ПРОЦЕССЕ ФОРМИРОВАНИЯ КОЛЛЕКТИВА КЛАССА
ЛИЧНОСТНОЕ РАЗВИТИЕ ОБУЧАЮЩИХСЯ В ПРОЦЕССЕ ФОРМИРОВАНИЯ КОЛЛЕКТИВА КЛАССА