Анализ состояния фондового рынка на основе многомерных копула-функций

Цель и задачи
Целью работы является исследование внутренней зависимости во временных рядах цен акций с помощью копула- и автокорреляционных функций.
Задачи:
Разработка методики применения многомерных копула-функций к анализу временных рядов курсов акций;
Построение статистических оценок трехмерных копула-функций и определение на их основе типа связи во временных рядах;
Построение автокорреляционных функций временных рядов;
Анализ результатов, полученных с помощью копула- и автокорреляционных функций.

Копула (лат. Copula-пара) — это функция многомерного распределения, определённая на n-мерном единичном кубе [0,1]n, такая, что каждое её маргинальное распределение равномерно на интервале [0,1].
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятыми со сдвигом по времени.
Автокорреляционная функция (АКФ) определяется интегралом:
и показывает связь функции с копией самой себя, смещенной на величину .
Основные определения

Независимая копула-функция:
С┴(u1…un)= u1*…*un.
Комонотонная копула-функция:
Cmax(u1…un)=min{u1…un}.
Эталонные копула-фунции

Берется временной ряд цен акций компании, а также два ряда, полученные из исходного с помощью сдвига на величины t1 и t2, находящиеся в промежутке от 1 до 10, причём t1 < t2.
Строится статистическая оценка трёхмерной копула-функции на решётке с шагом 1/N.
Дано:
- результаты наблюдений, где u0 - исходный временной ряд,
u1 и u2 -временные ряды, сдвинутые относительно исходного на величины t1 и t2,
n – число наблюдений (причем n>>N),
u0(i), u1(j) , u2(g) - соответствующие порядковые статистики,
n(i,j,g)/n – оценка значения копула-функции ,
где n(i,j,g) – число троек выборки ,
для которого выполняются неравенства:
Этапы исследования

3. Вычисляются расстояния до эталонной копула-функции C* , в качестве которой поочередно используются С┴ и Cmax. Расчет производится по формуле:
Строятся автокорреляционные функции:
Проводится сравнительный анализ расчётов, полученных с помощью копула- и автокорреляционных функций.
Этапы исследования

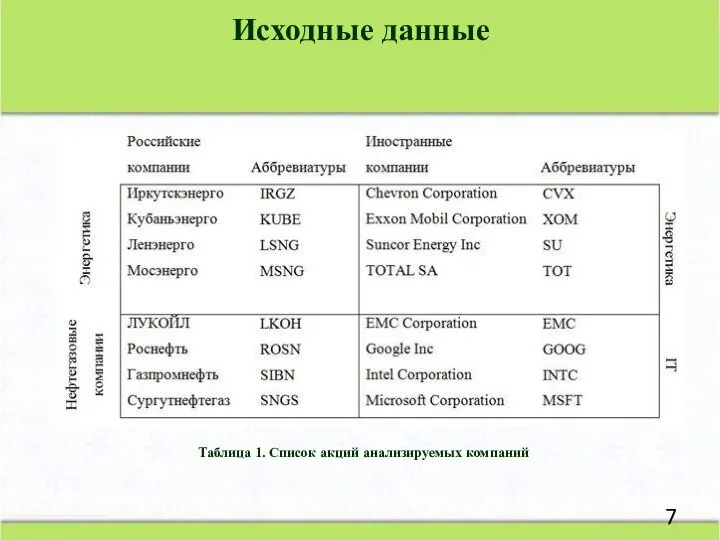
Исходные данные
Таблица 1. Список акций анализируемых компаний

Применение аппарата копула-функций для исследования акций Google Inc.
Таблицы 2. Суммы отклонений статистических оценок копула-функций от эталонных за 2008-2012гг
Таблица 3. Динамика связей в ряду данных в зависимости от макроэкономических факторов за 2008-2012гг
t2
t1

Рисунок 1. Динамика сумм отклонений расчетных копула-функций от комонотонной за 2008-2012 гг (для t1=3)
Применение аппарата копула-функций для исследования акций Google Inc.

Рисунок 2. Динамика сумм отклонений расчетных копула-функций от независимой за 2008-2012 гг (для t1=3)
Применение аппарата копула-функций для исследования акций Google Inc.

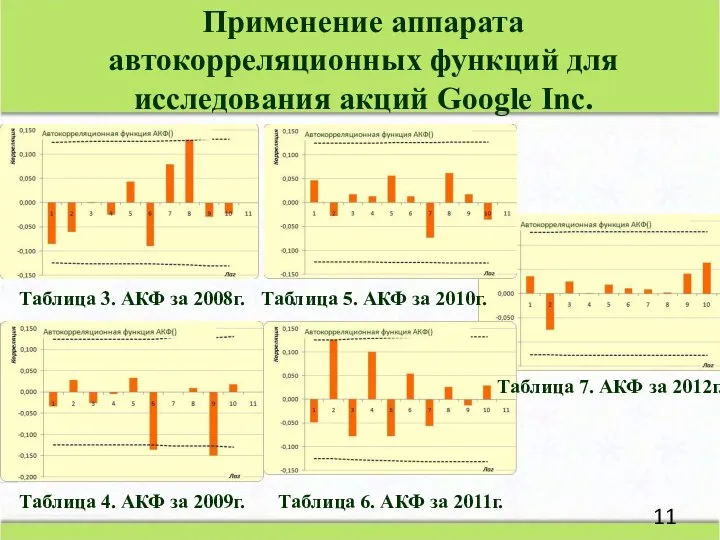
Таблица 3. АКФ за 2008г.
Таблица 4. АКФ за 2009г.
Таблица 5. АКФ за 2010г.
Таблица 6. АКФ за 2011г.
Таблица 7. АКФ за 2012г.
Применение аппарата автокорреляционных функций для исследования акций Google Inc.

Произведена оценка характера связи внутри временного ряда в зависимости от величины временных лагов с использованием копула-функций.
Было выявлено, что:
Комонотонная связь внутри ряда выражена сильнее, чем независимая.
Во время экономического подъёма во временном ряду усиливается независимость, а во время экономического спада – комонотонная связь между наблюдениями.
При увеличении комонотонной связи разброс расстояний до эталонных копула-функций при увеличении временных лагов уменьшается, то есть прогноз цены акции становится более обоснованным.
Были построены автокорреляционные функции и произведено сравнение результатов, полученных с помощью копула- и автокорреляционных функций.
Выводы

А. И. Авзалова, М.В. Филиппова. Исследование динамики цен акций с помощью копула-функций.
Молодой ученый:
ежемесячный научный журнал.
Том 2 №5(40)/2012.
Чита: ООО Молодой ученый.
С. 232-238

Спасибо за внимание!

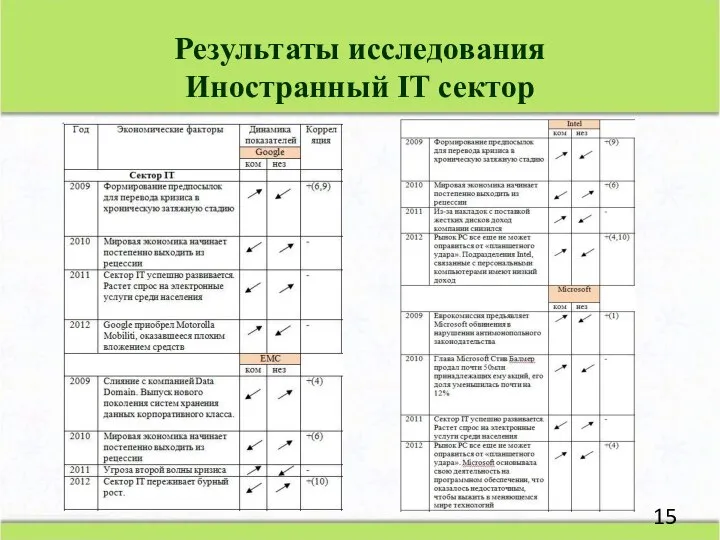
Результаты исследования
Иностранный IT сектор

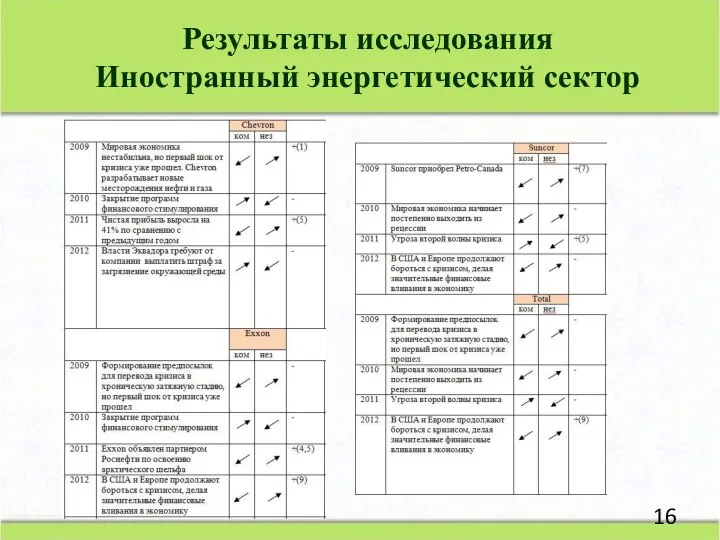
Результаты исследования
Иностранный энергетический сектор

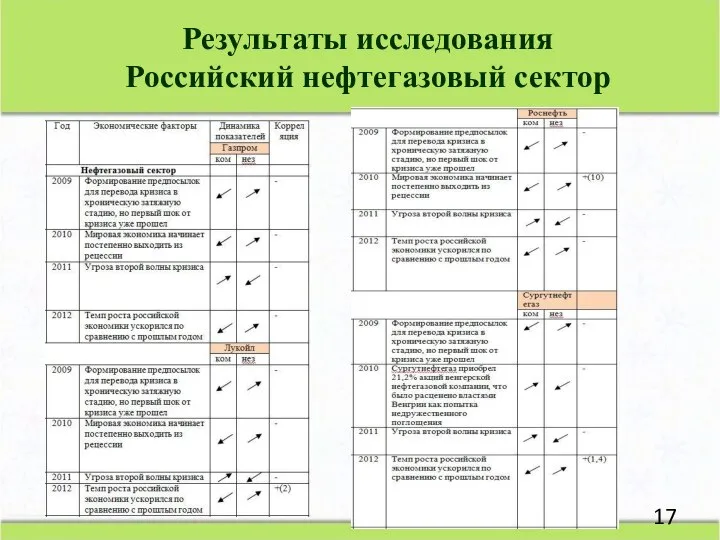
Результаты исследования
Российский нефтегазовый сектор