АНАШЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

ГРАФИКИ ФУНКЦИЙ,
СВЯЗАННЫХ С МОДУЛЕМ.
Занятие по элективному курсу «Избранные вопросы математики» в 11 классе.

ПОВТОРЕНИЕ:

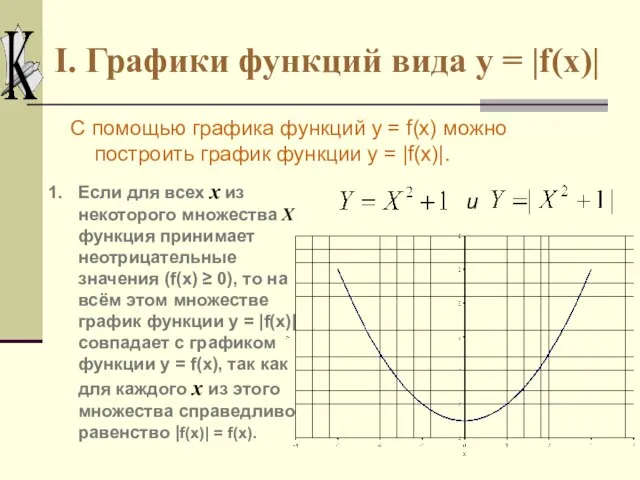
I. Графики функций вида y = |f(x)|
С помощью графика функций y = f(x) можно построить график функции y = |f(x)|.
Если для всех х из некоторого множества Х функция принимает неотрицательные значения (f(x) ≥ 0), то на всём этом множестве график функции y = |f(x)| совпадает с графиком функции y = f(x), так как для каждого х из этого множества справедливо равенство |f(x)| = f(x).
и

I. Графики функций вида y = |f(x)|
2. Если же для всех х из некоторого множества х1 функция y = f(x)
принимает отрицательные значения (f(x) < 0), то на этом множестве
график функции y = |f(x)| получается отражением графика функции
y = f(x) относительно оси Ох, так как для каждого х из этого множества справедливо равенство |f(x)| = - f(x).
Таким образом, для построения графика функции y = |f(x)| надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше этой оси, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.

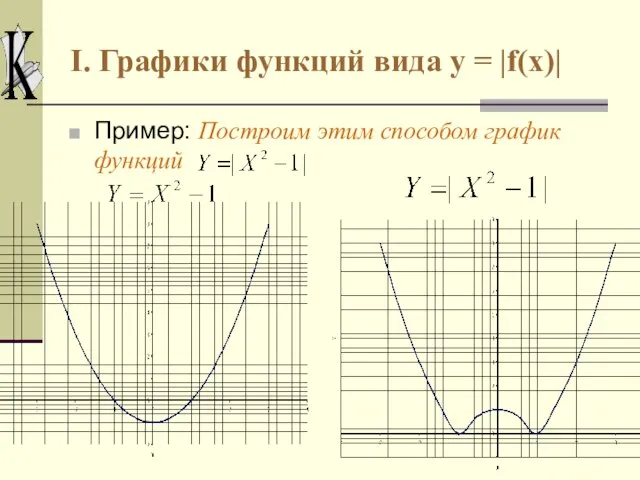
I. Графики функций вида y = |f(x)|
Пример: Построим этим способом график функций

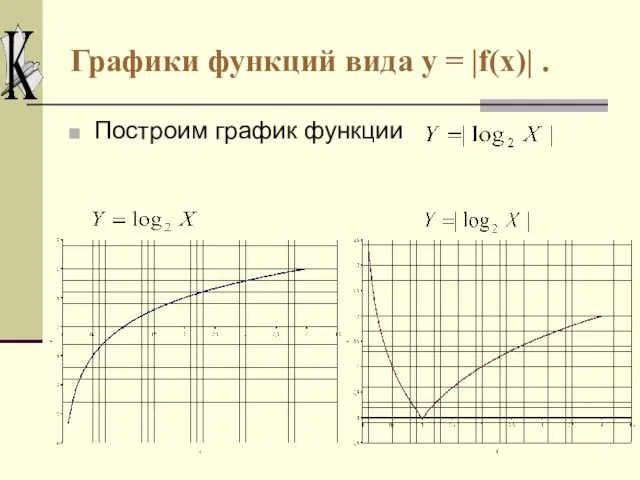
Графики функций вида y = |f(x)| .
Построим график функции

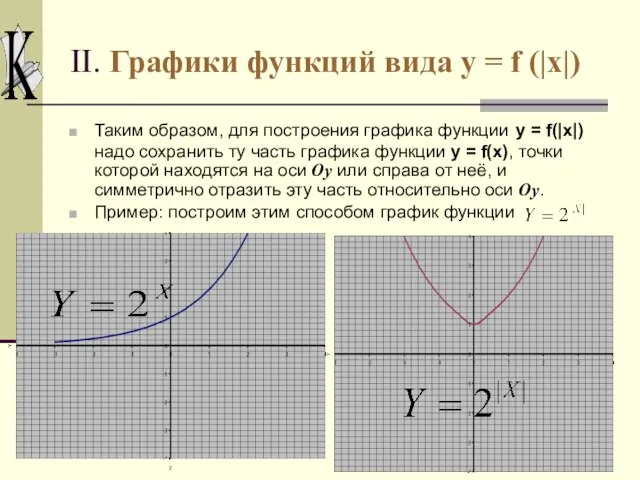
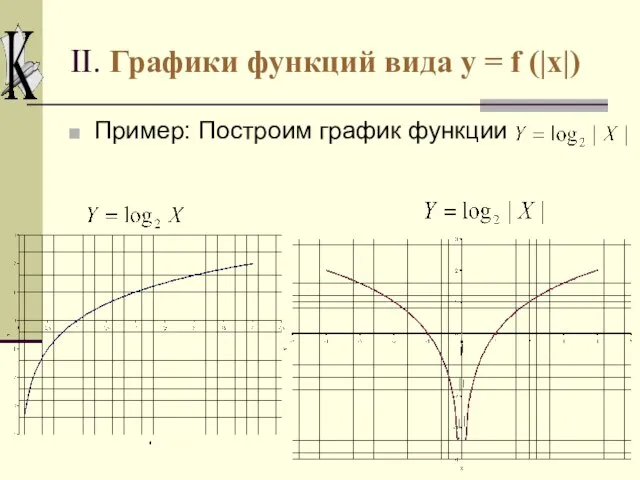
II. Графики функций вида y = f (|x|)
С помощью графика функции y = f(x) можно построить график функции y = f(|x|).
Заметим, что если точка х принадлежит области определения функции y = f(|x|) , то и точка – х также ей принадлежит, так как |-х| = |х|. Тогда для любого х из области определения функции y = f(|x|) справедливо равенство f(|-x|) = f(|x|) , то есть функция y = f(|x|) чётная.
Для всех x ≥ 0 график функции y = f(|x|) совпадает с графиком функции y = f(x), так как для каждого x ≥ 0 справедливо равенство f(|x|) = f(x). Эта правая часть графика, а левая часть графика симметрична правой относительно оси Оу, так как функция y = f(|x|) чётная.

II. Графики функций вида y = f (|x|)
Таким образом, для построения графика функции y = f(|x|) надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Оу или справа от неё, и симметрично отразить эту часть относительно оси Оу.
Пример: построим этим способом график функции

II. Графики функций вида y = f (|x|)
Пример: Построим график функции

Контрольное задание:
Постройте графики функций