Астрономические системы отсчета и методы их построения

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Основные Элементы:
Общая Теория Относительности (или альтернативная теория гравитации)
Калибровочная свобода
Мультипольные гравитационные поля
Пост-Ньютоновские приближения
Асимптотические сшивки полей
Теория систем отсчета: резолюции МАС 2000
Теория прецессии и нутации МАС 2000
Компьютерные коды: NASA GEODYNE, Orbit Determination Program, CALC VLBI, etc.

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Существующие стандарты
Общая Теория Относительности – резолюции МАС 2000
Устраняет нефизические степени свободы из наблюдаемых величин
Адекватная интерпретация гравитационных экспериментов
Параметризованный пост-Ньютоновский (ППН) формализм – морально устарел, требует модернизации. Причина:
Нединамичен
Системы отсчета не разработаны
Нековариантен
Калибровочные степени свободы перепутаны с физическими эффектами
Не вполне адекватен в интерпретации гравитационной физики и тестов ОТО

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Параметризованная теория систем отсчета:
Ковариантна
Калибровочно-инвариантна
Оперирут непосредственно с наблюдаемыми величинами
Исключает калибровочно-зависимые решения и эффекты

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочная свобода электродинамики
Полевые переменные эл.-эм. поля
Калибровочное преобразование
Калибровочная инвариантность эл.-эм. поля

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Полевые переменные в гравитодинамике
Метрический тензор
Афинная связность
Тензор кривизны

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочная инвариантность гравитодинамики

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Гармоническая калибровка и «остаточная» калибровочная свобода
Гармонические условия
Уравнения Эйнштейна
«Остаточная» калибровочная свобода

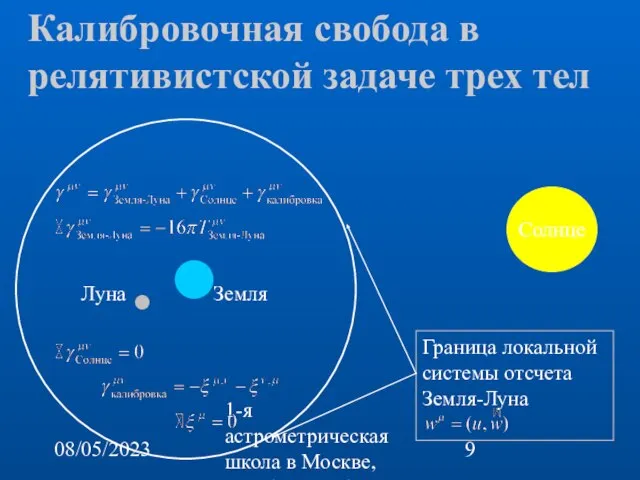
08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочная свобода в релятивистской задаче трех тел
Луна
Земля
Солнце
Граница локальной
системы отсчета
Земля-Луна

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочные степени свободы гравитационного поля в системе Земля-Луна

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Примеры калибровочной свободы:
TT-TCB преобразование времени
Лоренцево сокращение
Эйнштейновское сжатие
Релятивистская прецессия (de Sitter, Lense-Thirring, Thomas)

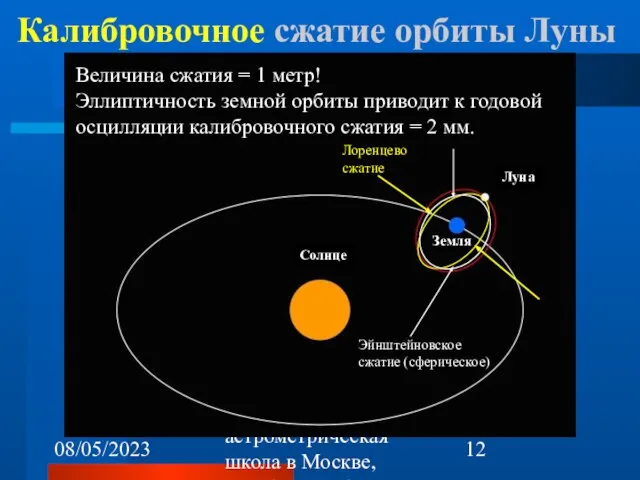
08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочное сжатие орбиты Луны
Величина сжатия = 1 метр!
Эллиптичность земной орбиты приводит к годовой
осцилляции калибровочного сжатия = 2 мм.
Земля
Лоренцево
сжатие
Эйнштейновское
сжатие (сферическое)
Солнце
Луна

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Являются ли калибровочные степени свободы наблюдаемыми?
Эйнштейн: нет – отсутствуют в наблюдаемых данных, не имеют отношения к физическим эффектам
Нордведт: да – отсутствуют в наблюдаемых данных, их отсутствие указывает на присутствие гравимагнитного поля (эффект «голого короля»)
Kopeikin, S., Phys. Rev. Lett., vol. 98, id. 229001 (2007)
The LLR technique involves processing data with two sets of mathematical equations, one related to the motion of the moon around the earth, and the other related to the propagation of the laser beam from earth to the moon. These equations can be written in different ways based on "gauge freedom," the idea that arbitrary coordinates can be used to describe gravitational physics. The gauge freedom of the LLR technique shows that the manipulation of the mathematical equations is causing JPL scientists to derive results that are not apparent in the data itself.

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Аберрация и сокращение размеров движущихся тел
В частности, это означает, что размер сферы, полученный при её фотографировании посредством параллельного пучка лучей, не будет зависеть от конкретного наблюдателя, и всегда будет равен размеру сферы на фотографии, сделанной в системе покоя сферы, то есть Δr′. Аберрация изменяет направление пучка лучей. Фотографическая пластинка должна быть поставлена так, чтобы лучи света падали на неё перпендикулярно. Протяженная двигающаяся сфера наблюдается как повернутая на некоторый угол (равный углу аберрации!); при этом наблюдаемое поперечное сечение сферы остается неизменным – то есть Лоренцево сокращение сферы не наблюдается!
Фотография
движущейся сферы

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Калибровочные степени свободы в уравнениях Эйнштейна-Инфельда-Гоффмана для системы Земля-Луна:
“Ньютоновские” преобразования релятивистской гравитационной 4-х силы
Устраняет все калибровочные степени свободы из преобразований координат!
Переводит все калибровочные степени свободы в уравнения движения Луны вокруг Земли, где они появляются как фиктивные (ненаблюдаемые) силы

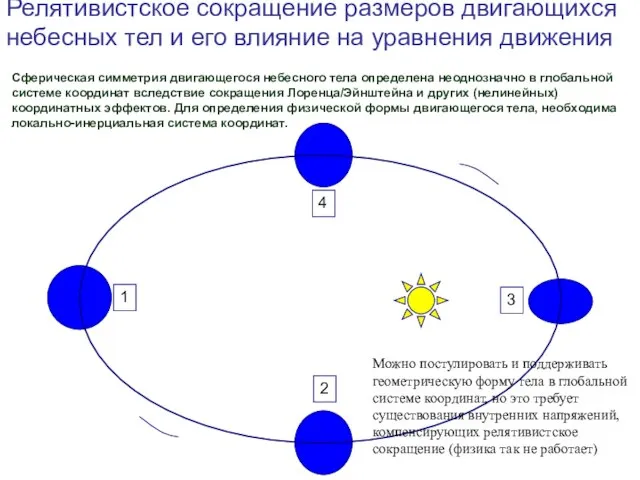
08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Сферическая симметрия двигающегося небесного тела определена неоднозначно в глобальной системе координат вследствие сокращения Лоренца/Эйнштейна и других (нелинейных) координатных эффектов. Для определения физической формы двигающегося тела, необходима локально-инерциальная система координат.
Можно постулировать и поддерживать
геометрическую форму тела в глобальной
системе координат, но это требует
существования внутренних напряжений,
компенсирующих релятивистское
сокращение (физика так не работает)
Релятивистское сокращение размеров двигающихся небесных тел и его влияние на уравнения движения

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Пример: постулат сферической симметрии тел в глобальной системе координат приводит к появлению фиктивной пост-Ньютоновской силы (Брумберг 1972; Копейкин и Власов 2004)

08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Выводы:
Калибровочная свобода в релятивистской гравитационной физике играет ключевую роль, но трудна для конкретного понимания
Неправильное истолкование калибровочной свободы влечет:
появление нефизических эффектов в уравнениях движения;
неправильной интерпретации наблюдаемых данных;
предложение ошибочных гравитационных экспериментов;
нефизическую трактовку прецесии и нутации, неправильным выводам о внутренней структуре Земли и Луны;
неточностям в построении навигационных систем и геодезических координатных сетей;
ошибкам в прецезионной космической навигации в ближнем и дальнем космосе
Внимательно изучаем труды классиков и осваиваем тонкости теорий, обладающих калибровочной свободой

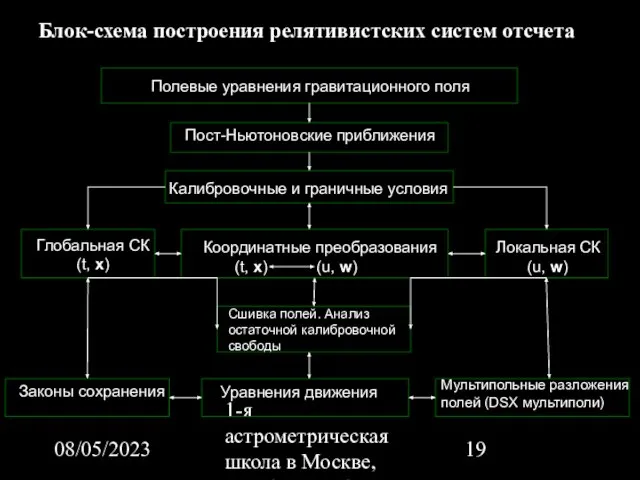
08/05/2023
1-я астрометрическая школа в Москве, октябрь 22-26, 2007
Блок-схема построения релятивистских систем отсчета
Полевые уравнения гравитационного поля
Пост-Ньютоновские приближения
Калибровочные и граничные условия
Глобальная СК
(t, x)
Локальная СК
(u, w)
Координатные преобразования
(t, x) (u, w)
Сшивка полей. Анализ
остаточной калибровочной
свободы
Законы сохранения
Уравнения движения
Мультипольные разложения
полей (DSX мультиполи)