БАЙЕСОВСКИЕ СЕТИ:

ПЛАН ИЗЛОЖЕНИЯ
Объект, предмет и контекст исследования
Обозначения
Вероятностная логика
Фрагменты знаний
Байесовские сети доверия (сжато)
Алгебраические байесовские сети
ФЗ АБС
непротиворечивость, априорный и апостериорный вывод, устойчивость
АБС
непротиворечивость, априорный и апостериорный вывод
Презентация Д.А. Никитина
Презентация С.И. Николенко
Применение байесовских сетей
Заключение

ОБЪЕКТ ИССЛЕДОВАНИЯ
Распределение вероятностей (или их семейство) над пропозициональными формулами, в общем виде представимое как

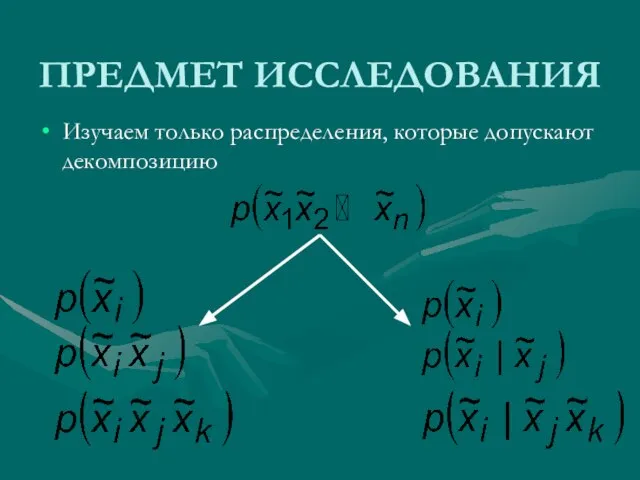
ПРЕДМЕТ ИССЛЕДОВАНИЯ
Изучаем только распределения, которые допускают декомпозицию

КОНТЕКСТ ИССЛЕДОВАНИЯ
Знания хранятся и передаются фрагментами (паттернами)
Атомарные высказывания о предметной области представляем пропозициональными формулами
Меру их истинности и тесноту связи между ним характеризуем с помощью вероятности
Фактически, мы пытаемся изучать один из возможных классов моделей баз фрагментов знаний с неопределенностью

ПРАГМАТИКА
Изучая свойства нашего предмета исследования и разрабатывая алгоритмы, мы опираемся на методы математики и теоретической информатики.
Тем не менее, наша конечная цель --- дать спецификацию программисту, чтобы он воплотил результаты исследований в программном приложении.
При этом алгоритмы и спецификации хотелось бы писать так, чтобы максимально учитывать достижения современной практической информатики: возможности сред разработки приложений, математических пакетов, алгоритмических библиотек…

НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
Аргументное место
Цепочка конъюнкций
Положит. означенная цеп. конъ.
Набор атомарных пропозиций
Кванты
Пропоз. формулы над множеством А
Идеал цепочек конъюнкций --- модель фрагмента знаний АБС

ЕСЛИ БЫТЬ ЧРЕЗМЕРНО ФОРМАЛЬНЫМ

ПРИМЕР (1)
.
,
,
,
.

ПРИМЕР (2)
.
,
,
,

ВЕРОЯТНОСТНАЯ ЛОГИКА
Подход по Н. Нильссону (1986 г.)
Более глубокая формализация дана в работах коллектива Фагина, Хальперна, Миггидо (пригодня для рассуждений об оценках сложности)
Другие глубокие формализации
Спор о приоритетах (de Finetti…)
Дж. Буль --- тоже писал о вероятности пропозиции

НАБОР ПРОПОЗИЦИЙ

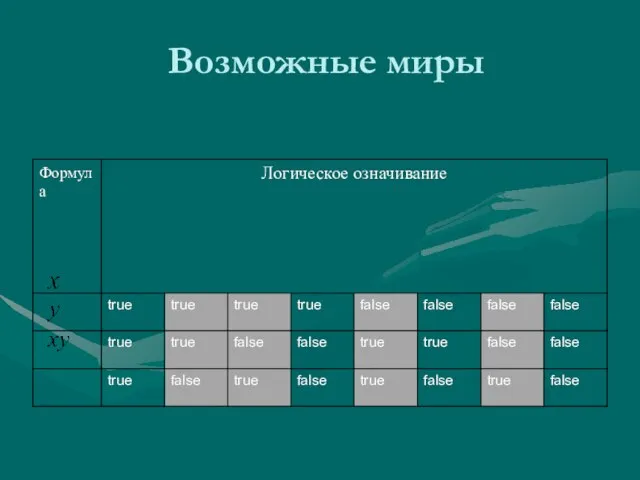
Возможные миры

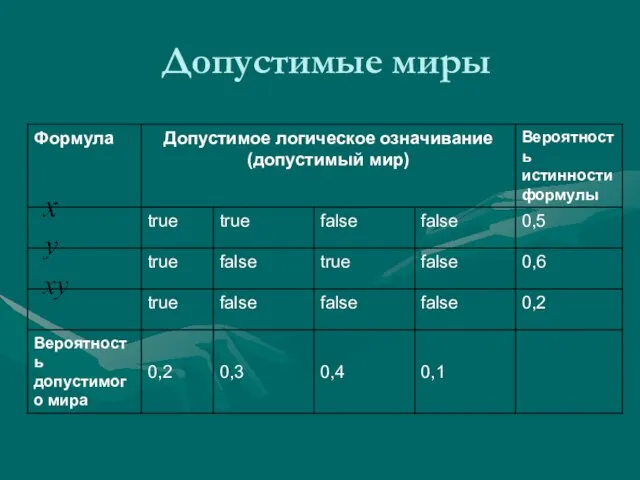
Допустимые миры

Вероятность истинности
В рамках подхода Н. Нильссона мы рассуждаем о вероятности истинности пропозиции;
Для краткости говорят вероятность пропозиции

Подход Н. Нильссона
Формальное изложение

Теорема о СДНФ

КВАНТЫ:
Множество элементарных событий

ВЕРОЯТНОСТЬ ПРОПОЗИЦИИ

ФРАГМЕНТ ЗНАНИЙ

ФЗ --- ФИЛОСОФИЯ ВОПРОСА
Эксперты связывают 1—2—3… пропозиции в своих рассуждениях (свойство переработки, передачи, хранения знаний человеком)
В статистике мы можем с какой-то степенью уверенности рассуждать об 1—2—3… пропозициях (иначе придется делать объем выборки слишком большим)
Фактически нам приходится рассуждать о наборах (базах) фрагментов знаний с неопределенностью
А работаем мы с различными моделями фрагментов знаний (моделями моделей предметной области)

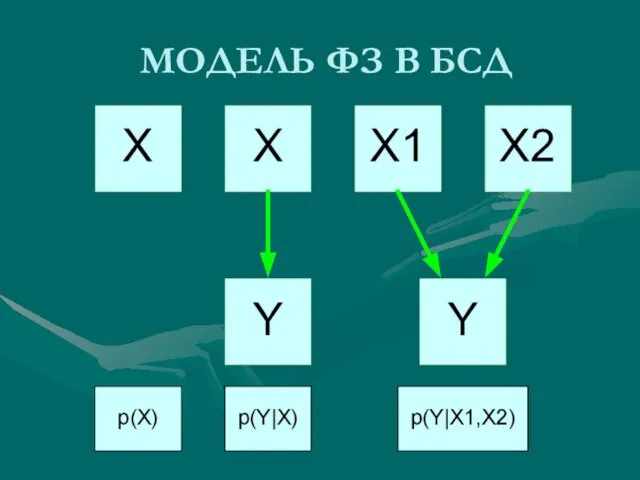
МОДЕЛЬ ФЗ В БСД

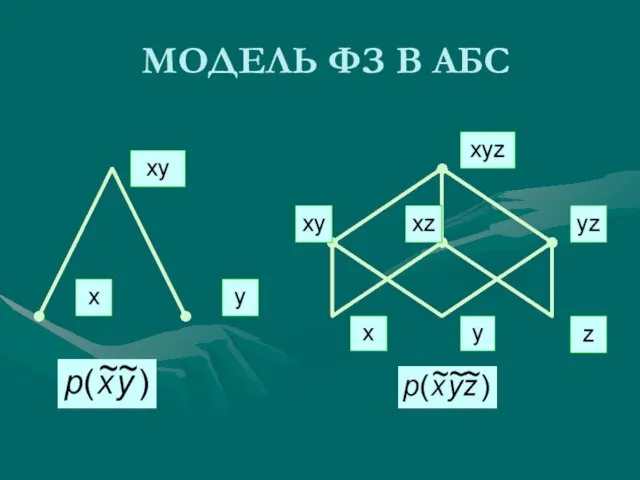
МОДЕЛЬ ФЗ В АБС

БАЙЕСОВСКИЕ СЕТИ ДОВЕРИЯ
В необходимом объеме (максимально сжатом)

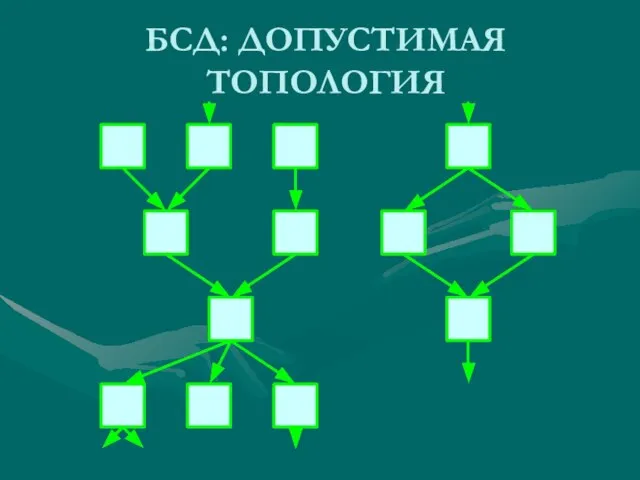
БСД: ДОПУСТИМАЯ ТОПОЛОГИЯ

БСД: FEEDBACK CYCLES

АЛГЕБРАИЧЕСКИЕ БАЙЕСОВСКИЕ СЕТИ

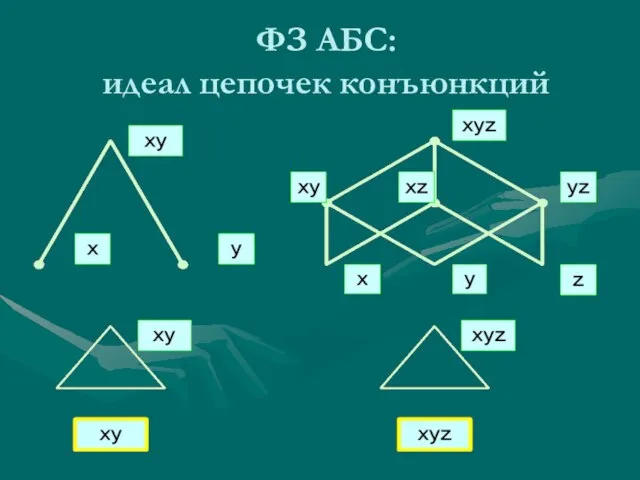
ФЗ АБС:
идеал цепочек конъюнкций

ОПЕРАЦИИ В ФЗ АБС
Поддержание непротиворечивости
Априорный вывод
Апостериорный вывод
Анализ устойчивости (чувствительности)

НЕПРОТИВОРЕЧИВОСТЬ ФЗ АБС

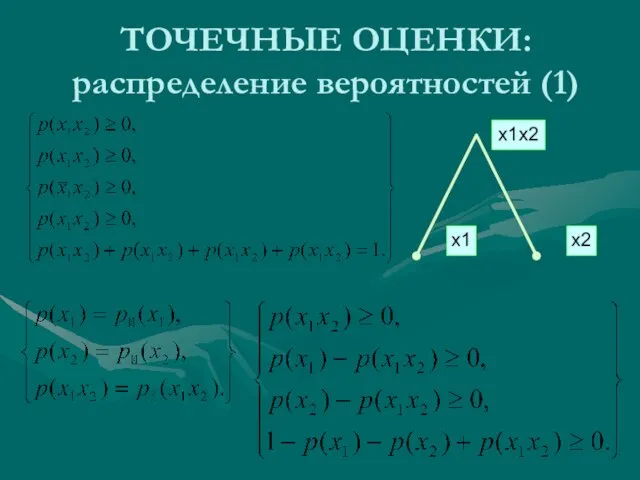
ТОЧЕЧНЫЕ ОЦЕНКИ:
распределение вероятностей (1)

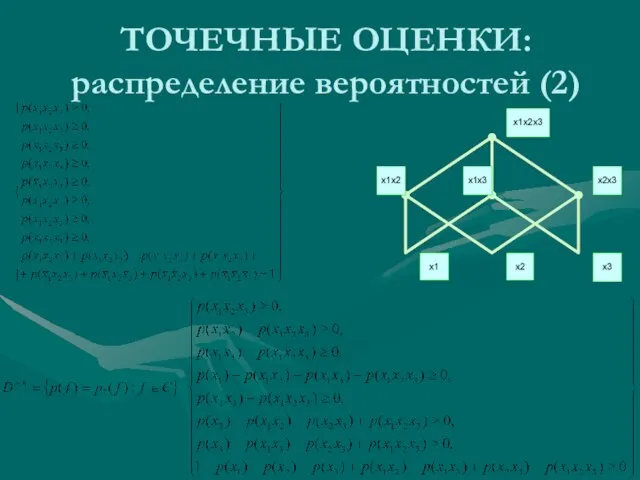
ТОЧЕЧНЫЕ ОЦЕНКИ:
распределение вероятностей (2)

ИНТЕРВАЛЬНЫЕ ОЦЕНКИ:
семейство распределений(1)

ИНТЕРВАЛЬНЫЕ ОЦЕНКИ:
семейство распределений (2)

ИНТЕРВАЛЬНЫЕ ОЦЕНКИ:
поддержание непротиворечивости

АПРИОРНЫЙ ВЫВОД В ФЗ

АПРИОРНЫЙ ВЫВОД: точечные оценки
Вероятность любой формулы, построенной над атомарными пропозициями из заданного ФЗ, можно линейно выразить через вероятности элементов этого ФЗ.
В точечном случае, таким образом, априорный вывод сводится к прямому вычислению вероятности новой пропозиции через вероятности известных.

АПРИОРНЫЙ ВЫВОД: интервальные оценки
Вероятность любой формулы, построенной над атомарными пропозициями из заданного ФЗ, можно линейно выразить через вероятности элементов этого ФЗ.
В интервальном случае вероятность новой формулы придется рассмотреть как целевую функцию соответствующей ЗЛП, найти максимум и минимум этой функции
В результате решения оптимизационной задачи будет получена интервальная оценка вероятности истинности новой формулы.

АПОСТЕРИОРНЫЙ ВЫВОД В ФЗ

СВИДЕТЕЛЬСТВО
Детерминированное свидетельство:
Недетерминированное свидетельство

КОРТЕЖ СВИДЕТЕЛЬСТВ
Детерминированные свидетельства:
Недетерминированные свидетельства

ДВЕ ЦЕЛИ
апостериорного вывода
Оценка вероятности свидетельства (кортежа свидетельств) над заданным ФЗ
Оценка апостериорных вероятностей элементов ФЗ при заданном свидетельстве (кортеже свидетельств)

АПОСТЕРИОРНЫЙ ВЫВОД:
формулы
… более подробно возникающие задачи оптимизации будут рассмотрены в специальной части презентации (Д. А. Никитин)

УСТОЙЧИВОСТЬ
(чувствительность)

УСТОЙЧИВОСТЬ ПРОЦЕССОВ:
«философия» вопроса
Поддержание непротиворечивости
Априорный вывод
Апостериорный вывода

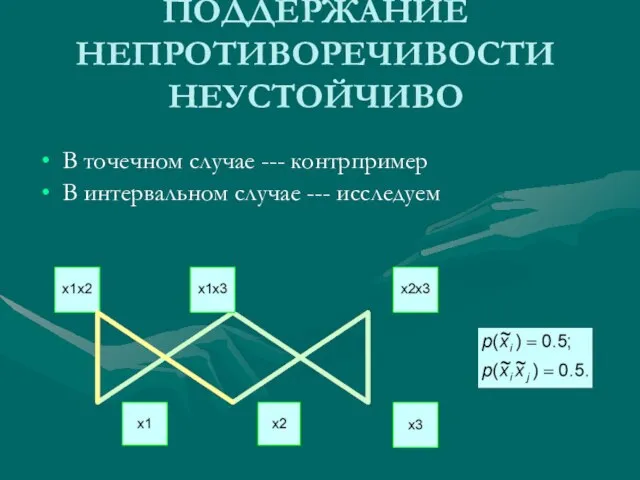
ПОДДЕРЖАНИЕ НЕПРОТИВОРЕЧИВОСТИ НЕУСТОЙЧИВО
В точечном случае --- контрпример
В интервальном случае --- исследуем

АПРИОРНЫЙ ВЫВОД УСТОЙЧИВ
Вычислительные эксперименты показывают устойчивость как в случае точечных, так и в случае интервальных оценок (относительно допустимых вариаций)
Показатели, на которые мы опираемся:
Изменение результата вывода (т.сл.)
Изменение границ результата вывода (и. сл.)
Изменение величины интервала, представляющего результат (и. сл.)
Эмпирическое определение показателей сводится к решению задач линейного программирования

Апостериорный вывод: поиск показателей устойчивости
Относительно чего устойчивость
Что можно «варьировать», «допустимо варьировать», как это формализовать
Изменение каких целевых переменных отслеживать
Какие (метрические) пространства выбирать (хотим получать удобные задачи оптимизации)

АЛГЕБРАИЧЕСКИЕ БАЙЕСОВСКИЕ СЕТИ
(АБС)

АБС: определение
Алгебраическая байесовская сеть состоит множества идеалов цепочек конъюнкций, построенных над подмножествами одного и того же множества атомарных пропозициональных формул. Идеалы могут иметь общие элементы.
Как правило рассматривают только связные АБС, поскольку компоненты связности можно рассмотреть как отдельные самостоятельные АБС.

АБС: изображение детализированное

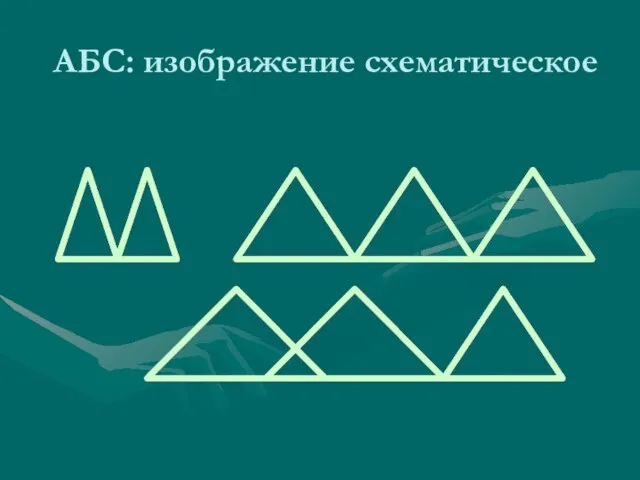
АБС: изображение схематическое

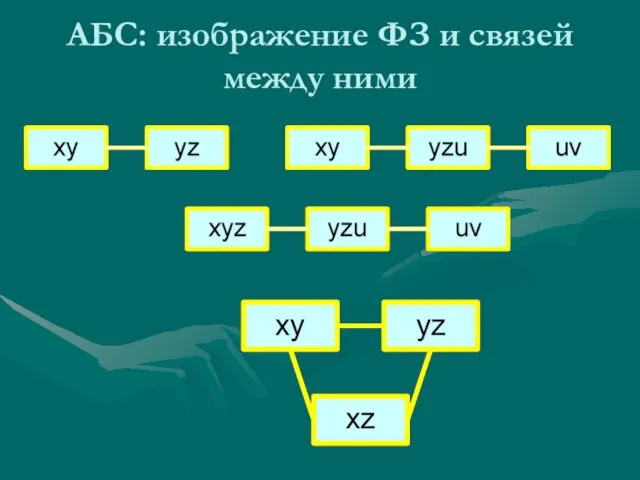
АБС: изображение ФЗ и связей между ними

АБС: степени непротиворечивости
Непротиворечивость локальная
Непротиворечивость внутренняя
Непротиворечивость внешняя
Непротиворечивость в целом
k-непротиворечивость

АБС: локальная непротиворечивость
АБС еще и нет
Непротиворечив каждый отдельный ФЗ, вошедший в АБС

Внутренняя и внешняя непротиворечивость
Неожиданное открытие

Внутренняя непротиворечивость АБС
Ранее использовавшееся определение
… когда выполняется требование локальной непротиворечивости, и оценка каждого отдельного элемента, входящего в более чем один ФЗ, согласована;

Внешняя непротиворечивость АБС
Ранее использовавшееся определение
… когда выполнено требование локальной непротиворечивости и оценки, требующие согласования, рассматриваются все вместе

Формализация «согласия»
А что такое --- оценки совпадают?
Первый подход: для одного и того же элемента, входящего в разные идеалы цепочек конъюнкций, его оценки во всех этих идеалах, совпадают;
Второй подход: для одного и того же элемента, входящего в разные идеалы цепочек конъюнкций, его оценки во всех этих идеалах, совпадают; кроме того, мы рассматриваем только те распределения вероятностей, которые совпадают на общих элементах идеалов, удовлетворяя при этом всем ограничениям, наложенным во соответствующих иделалах.

Интересный контрпример
Рассмотрим два «расширенных» идеала: один --- над u, v, w, x, а другой --- над v, w, x, y.
Пусть заданы в каждом идеале соттветсвенно заданы ограничения:
p(v)+p(w)+p(x)>= 1.6;
p(v)+p(w)+p(x)<= 1.5.
Тогда интервальные оценки любого элемента этих идеалов остануться [0;1].
Эти идеалы непротиворечивы по первому подходу, но противоречивы (абсолютно) по второму подходу.

Интересный контрпример (*)
Внешне противоречий не видно, а при совместном рассмотрении --- несовместные оценки.
Но пример касается некоторого «расширения» ФЗ.
Как ведет себя распределения вероятностей на идеалах цепочек конъюнкций --- исследуем.

Новая «внешняя» непротиворечивость
Накладываем ограничение только на «внешние признаки», т.е. так, чтобы границы интервалов совпадали

Новая «внутренняя» непротиворечивость
Требуется совпадение распределений, а не только границ интервалов.

Непротиворечивость в целом
В точечном случае
В интервальном случае

Ациклическая АБС
Из новой «внутренней» непротиворечивости следует непротиворечивость в целом

Априорный вывод в АБС

Формула над ФЗ
Поиск априорной оценки истинности формулы осуществляется как в отдельно взятом ФЗ

Формула над несколькими ФЗ
Над участвующими ФЗ надстраиваем ФЗ, их объемлющий; далее рассуждаем как для случая с отдельно взятым ФЗ;
Получить оценки верхней и нижней границы формулы через уже имеющиеся переменные, не надстраивая объемлющий ФЗ; ()
Разложить формулу в СДНФ, оценить каждого кванта из СДНФ на основе апостериорного вывода; ()
Приближенные оценки (например, на основе работы с минимальными элементами); ()

Апостериорный вывод
Базируется на выводе в отдельно взятом ФЗ
В определенном смысле используется метод «пропагации» (т.е. распространения, продвижения) свидетельств

«Идеальная» организация апостериорного вывода в ФЗ
Свидетельство входит по одним переменным;
Вероятности внутри ФЗ пересчитываются;
Новое «свидетельство» выходит по наборам переменных, общих с другими ФЗ

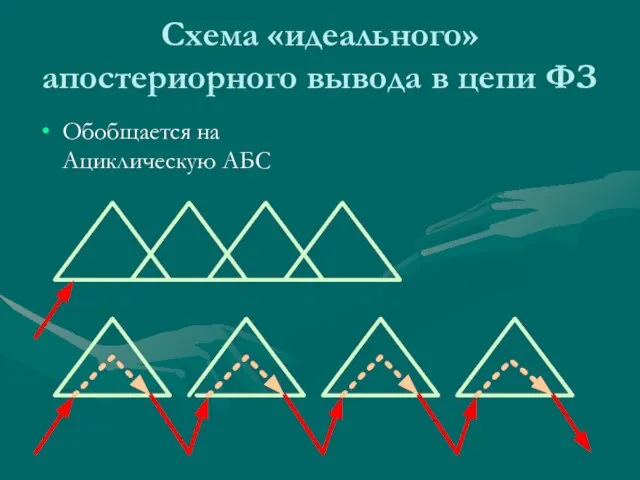
Схема «идеального» апостериорного вывода в цепи ФЗ
Обобщается на Ациклическую АБС

АБС и БСД
В случае точечных оценок при соблюдении гипотезы условной независимости существует алгоритм апостериорного вывода над АБС для кортежа детерминированных свидетельств.
БСД над пропозициями можно конвертировать в ациклическую АБС с точечными оценками; результаты вывода в БСД и апостериорного вывода в такой АБС будут совпадать

Проблема циклов
Циклы погружаются в объемлющий ФЗ
Циклы разрываются, если соответствующие наборы переменных независимы
Приближенные методы: степени согласованности оценок, полученных разными путями
Вопросы, связанные с обработкой циклов, требуют еще очень большой работы