bda8428bad5e4516a9f1726e635d7bab

Математический диктант

1. Выбери правильный ответ
Тангенсом ( котангенсом) острого угла прямоугольного
треугольника называется отношение:
а) противолежащего катета к прилежащему катету;
б) прилежащего катета к гипотенузе;
в) противолежащего катета к гипотенузе;
г) прилежащего катета к противолежащему катету;
Вариант 1 (2)

2. Используя рисунок, выбери правильный ответ
а)
б)
в)
г)
а)
б)
в)
г)

3. Используя рисунок, выбери правильный ответ
а)
б)
в)
г)
а)
б)
в)
г)

4. Для треугольника АВС, какое справедливо равенство:
а)
б)
а)
в)
г)
б)
в)
г)

Что общего на этих рисунках?

05. 04. 19
Классная работа
Определение подобных треугольников

Определение
Подобные фигуры - это фигуры, имеющие одинаковую форму, но различные размеры.

Например
Подобны две фотографии, отпечатанные с одного негатива, но с разными увеличениями.

Например
Подобны архитектурное сооружение и его макет.

Например
Подобны животное и его игрушечная фигурка .

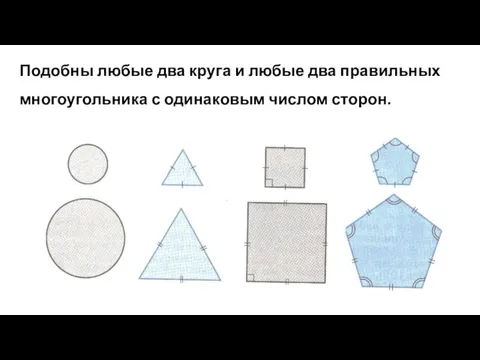
Подобны любые два круга и любые два правильных многоугольника с одинаковым числом сторон.

Из этих примеров можно увидеть, что соответствующие линейные размеры одной фигуры, подобной некоторой другой фигуре, в одно и то же число раз меньше или больше линейных размеров другой фигуры.

Так, на коробках игрушечных моделей самолётов указано, во сколько раз их детали меньше соответствующих деталей настоящих самолётов.
Поэтому все размеры одной из двух подобных фигур получают, умножая на некоторое число соответствующие размеры другой из них.

Определение
Два треугольника называются подобными, если стороны одного из них получаются из сторон другого умножением на некоторый множитель, т. е. стороны одного треугольника пропорциональны сторонам другого треугольника.

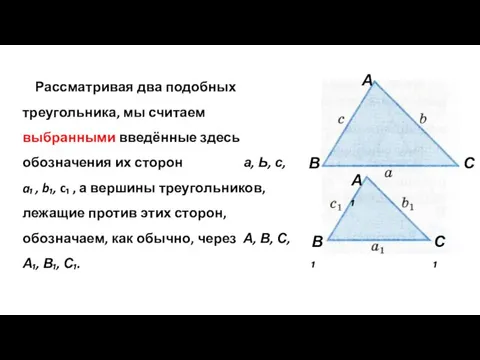
Рассматривая два подобных треугольника, мы считаем выбранными введённые здесь обозначения их сторон а, Ь, с, a₁ , b₁, c₁ , а вершины треугольников, лежащие против этих сторон, обозначаем, как обычно, через А, В, С, А₁, В₁, С₁.
А
В
С
А₁
В₁
С₁

А
В
С
А₁
В₁
С₁

А1
B1
C1
А
B
C

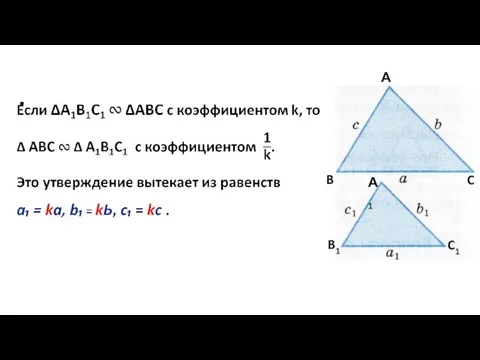
Если к = 1, то треугольники равны.
Поэтому равенство треугольников — это частный случай подобия треугольников (с коэффициентом подобия, равным единице).

Вопросы для самоконтроля
Какие фигуры называются подобными?
Какие треугольники называются подобными?
Что такое коэффициент подобия?
Верно ли, что равные треугольники подобны? Равны ли подобные тре­угольники?

Дополняем теорию
№ 9.1; № 9.2; № 9.3

№ 9.1
Прямоугольные треугольники, имеющие соответственно равные острые углы, подобны.

№ 9.2
Отношение периметров подобных треугольников равно коэффициенту подобия.

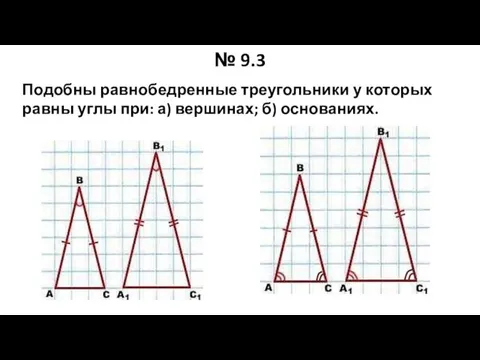
№ 9.3
Подобны равнобедренные треугольники у которых равны углы при: а) вершинах; б) основаниях.