Белорусский государственный университет Факультет прикладной математики и информатики Кафедра методов оптимального управления
Содержание
- 2. Поставленные цели и задачи Изучить структуру опоры для задачи в классе ИУВ-1 Построить опору для задачи
- 3. Поставленные цели и задачи Реализовать моделирование режима реального времени Провести сравнительный анализ программного и позиционного управления
- 4. Объект исследования. Методы исследования. Область применения Объект исследования – задачи в классах инерционных управляющих воздействий Методы
- 5. Актуальность Возможность построения реализации оптимальной обратной связи позволит управлять системой в режиме реального времени, корректировать это
- 6. Инерционные управляющие воздействия первого порядка. Постановка задачи Пусть промежуток управления. Скалярную функцию u(t), назовем инерционным
- 7. Задача с фазовыми ограничениями Если ввести дополнительную фазовую переменную , то задачу (2) можно трактовать как
- 8. Эквивалентная функциональная форма Задача (2) эквивалентна следующей задаче линейного программирования (ЛП) (4) элементы которой вычисляются с
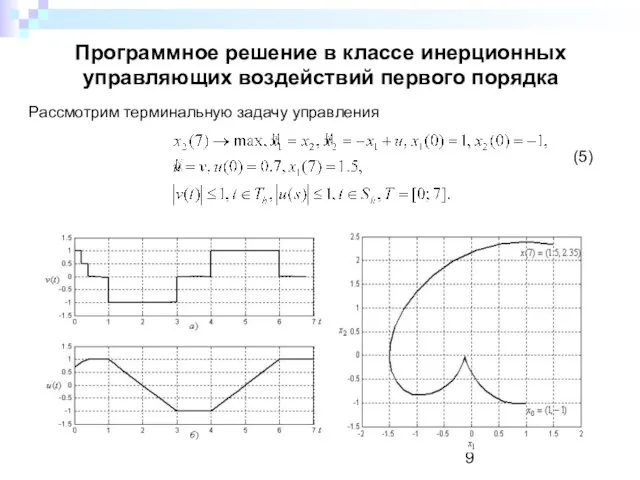
- 9. Программное решение в классе инерционных управляющих воздействий первого порядка Рассмотрим терминальную задачу управления (5)
- 10. Позиционное решение Для того, чтобы ввести понятие позиционного решения, рассматриваемую в классе инерционных управлений терминальную задачу
- 11. Оптимальная обратная связь Функцию (8) назовем оптимальным управляющим сигналом типа (дискретной) обратной связи в задаче (6).
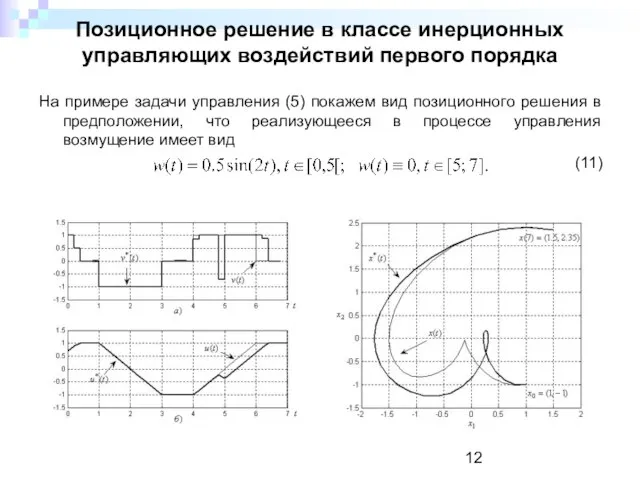
- 12. Позиционное решение в классе инерционных управляющих воздействий первого порядка На примере задачи управления (5) покажем вид
- 13. Моделирование режима реального времени На примере задачи в классе инерционных управлений первого порядка (12) проиллюстрируем влияние
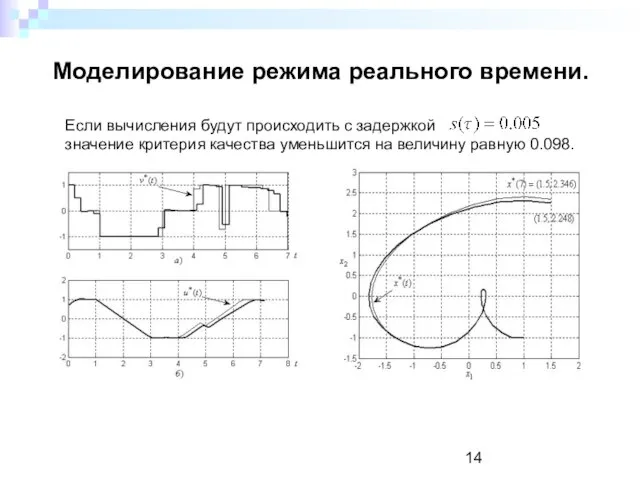
- 14. Моделирование режима реального времени. Если вычисления будут происходить с задержкой значение критерия качества уменьшится на величину
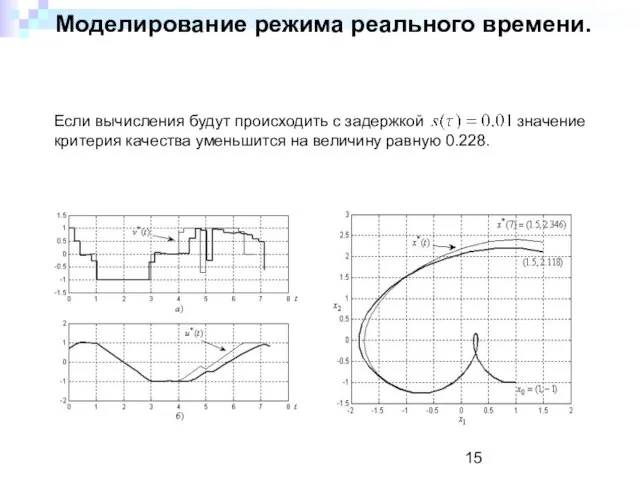
- 15. Моделирование режима реального времени. Если вычисления будут происходить с задержкой значение критерия качества уменьшится на величину
- 16. Инерционные управляющие воздействия второго порядка. Постановка задачи Пусть промежуток управления. Скалярную функцию u(t), назовем инерционным
- 17. Задача с фазовыми ограничениями Если ввести дополнительные фазовые переменные , то задачу (14) можно трактовать как
- 18. Эквивалентная функциональная форма Задача (14) эквивалентна следующей задаче линейного программирования (ЛП) (16) элементы которой вычисляются с
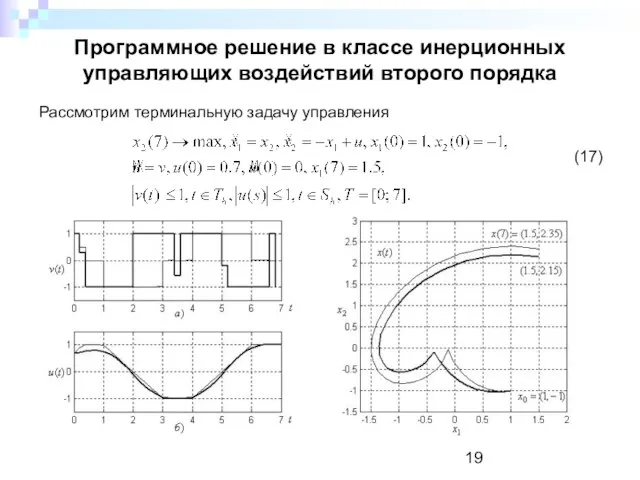
- 19. Программное решение в классе инерционных управляющих воздействий второго порядка Рассмотрим терминальную задачу управления (17)
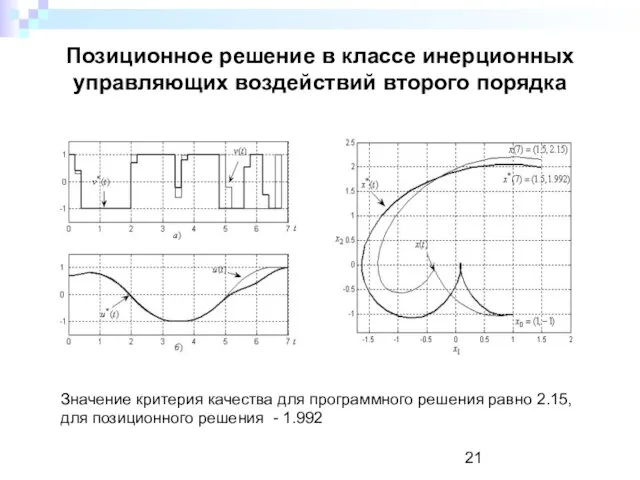
- 20. Позиционное решение в классе инерционных управляющих воздействий второго порядка В классе инерционных управляющих воздействий второго порядка
- 21. Позиционное решение в классе инерционных управляющих воздействий второго порядка Значение критерия качества для программного решения равно
- 22. Заключение В данной работе исследованы терминальные задачи ОУ в классе инерционных управлений первого и второго порядков
- 23. Опуликованность результатов Тезисы совместного с Н.С. Павленок доклада опубликованы в сборнике конференции «Еругинские чтения - 2009»
- 25. Скачать презентацию
















 phpgC5XEp_Cifra-3
phpgC5XEp_Cifra-3 Умирающие и их родственники (72-74)
Умирающие и их родственники (72-74) Автоматизация звука Л в слогах
Автоматизация звука Л в слогах Маркетинг территории. Город Тюмень
Маркетинг территории. Город Тюмень Проект «ОРГАНИЗАЦИЯ ПОХОДОВ КАК СОВМЕСТНАЯ ДОСУГОВАЯ ДЕЯТЕЛЬНОСТИ ДЕТСКОГО САДА С СЕМЬЯМИ ВОСПИТАННИКОВ»
Проект «ОРГАНИЗАЦИЯ ПОХОДОВ КАК СОВМЕСТНАЯ ДОСУГОВАЯ ДЕЯТЕЛЬНОСТИ ДЕТСКОГО САДА С СЕМЬЯМИ ВОСПИТАННИКОВ» Изготовление скворечника
Изготовление скворечника Этимология названий птиц
Этимология названий птиц Презентация на тему Специфика изображений в полиграфии по искусству 9 класс
Презентация на тему Специфика изображений в полиграфии по искусству 9 класс Второй закон Ньютона
Второй закон Ньютона Пахать и строить, все оно может,Если ему уголек в том поможет.
Пахать и строить, все оно может,Если ему уголек в том поможет. Шегарашы
Шегарашы Предвыборная программа кандидата на пост председателя студенческого совета ИРТСУ, Пацюк Тимура Тимофеевича
Предвыборная программа кандидата на пост председателя студенческого совета ИРТСУ, Пацюк Тимура Тимофеевича 258 Ты был юношей на свете
258 Ты был юношей на свете Основы государственного регулирования таможенного дела и таможенной политики в Российской Федерации
Основы государственного регулирования таможенного дела и таможенной политики в Российской Федерации Гипертекстовые технологии в Microsoft Word 2007
Гипертекстовые технологии в Microsoft Word 2007 Особенности физико-географического положения России
Особенности физико-географического положения России Причины развода
Причины развода به نام خدا
به نام خدا Диалоги об амфибиях
Диалоги об амфибиях Петровское барокко
Петровское барокко Тим Собакин
Тим Собакин Развитие биотехнологии в Республике Татарстан
Развитие биотехнологии в Республике Татарстан Пробелы в области юридических и иных знаний у сотрудников таможенных органов
Пробелы в области юридических и иных знаний у сотрудников таможенных органов Большая премена
Большая премена Свойства живых организмов
Свойства живых организмов Картины Рериха
Картины Рериха Форум СоТружество Молодежи
Форум СоТружество Молодежи Алгебраические дроби
Алгебраические дроби