Содержание
- 2. Электрические цепи Тема№1: Электрические цепи постоянного тока Тема№2: Электрические цепи синусоидального тока Тема№3: Трёхфазные цепи
- 3. Тема №1: Электрические цепи постоянного тока. Основные понятия и определения. Элементы электрической цепи и её топология.
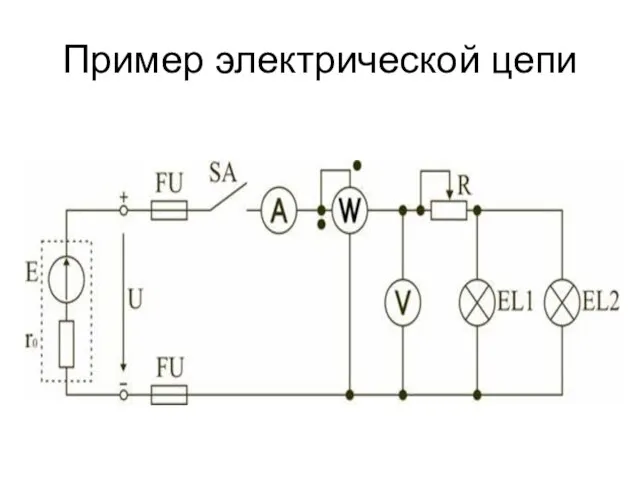
- 4. Пример электрической цепи
- 5. Источник электрической энергии Источником электрической энергии (питания) называется устройство, преобразующее какой-либо вид энергии в электрическую. Источники,
- 6. Постоянный электрический ток Постоянным электрическим током называется ток, который с течением времени не меняет величину и
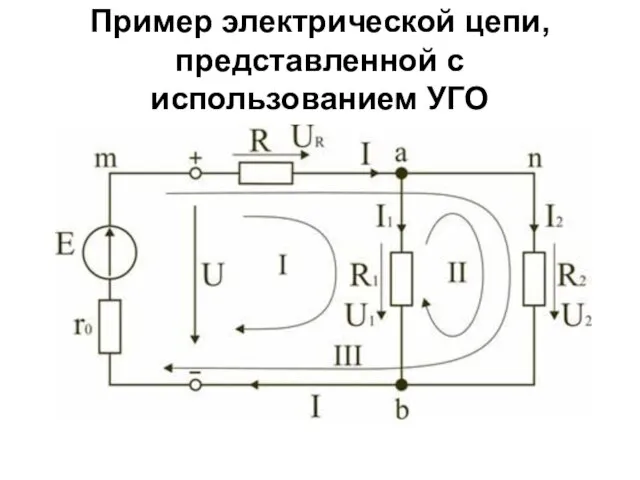
- 7. Пример электрической цепи, представленной с использованием УГО
- 8. Элементы электрической цепи и её топология Ветвь электрической цепи (схемы) – участок цепи с одним и
- 9. Выбор направлений E, U, I Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений
- 10. Линейные и нелинейные электрические цепи Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от
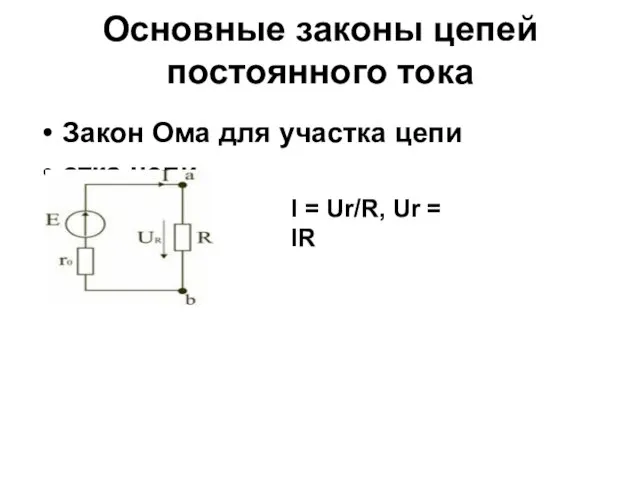
- 11. Основные законы цепей постоянного тока Закон Ома для участка цепи стка цепи I = Ur/R, Ur
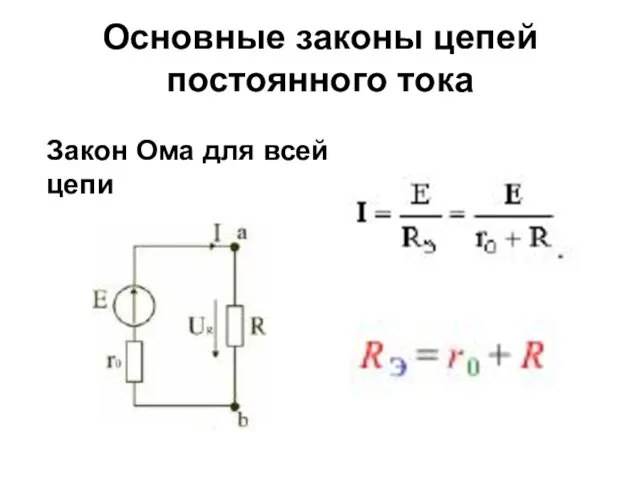
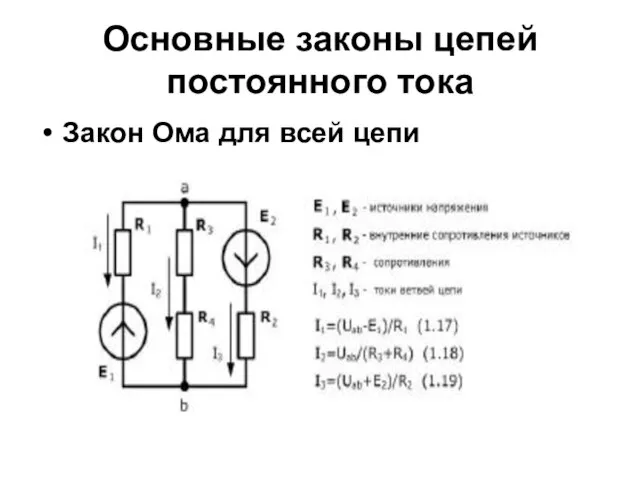
- 12. Основные законы цепей постоянного тока Закон Ома для всей цепи
- 13. Основные формулы по теме
- 14. Основные законы цепей постоянного тока Закон Ома для всей цепи
- 15. Основные законы цепей постоянного тока Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в узле
- 16. Основные законы цепей постоянного тока Второй закон Кирхгофа - в любом контуре электрической цепи алгебраическая сумма
- 17. Электрическая энергия и мощность источника питания В действующей цепи электрическая энергия источника питания преобразуется в другие
- 18. Баланс мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока
- 19. Основные формулы по теме
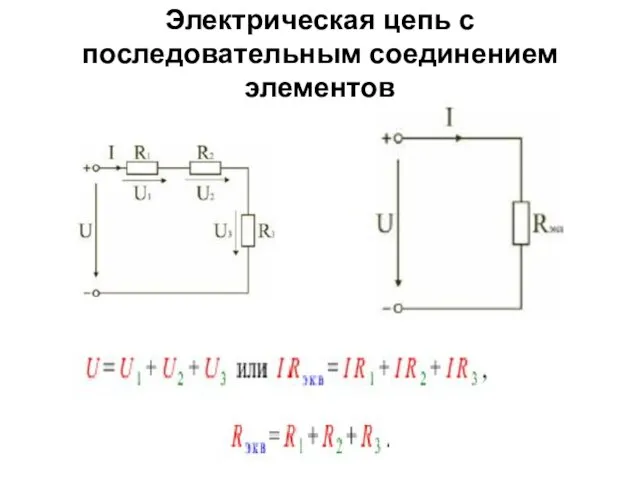
- 20. Электрическая цепь с последовательным соединением элементов
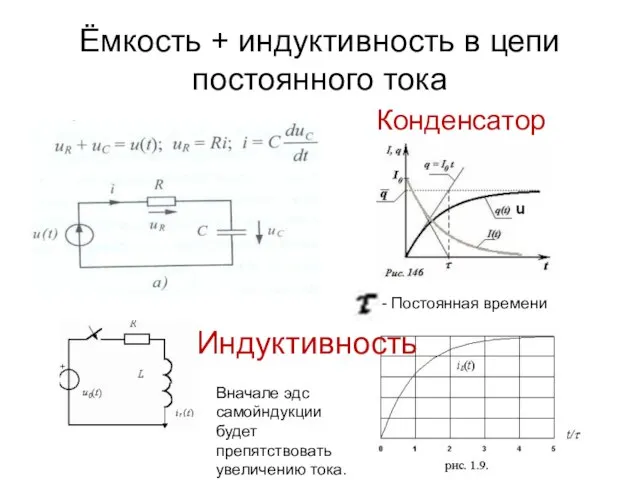
- 21. Ёмкость + индуктивность в цепи постоянного тока Конденсатор Индуктивность - Постоянная времени Вначале эдс самойндукции будет
- 22. Электрические цепи синусоидального тока
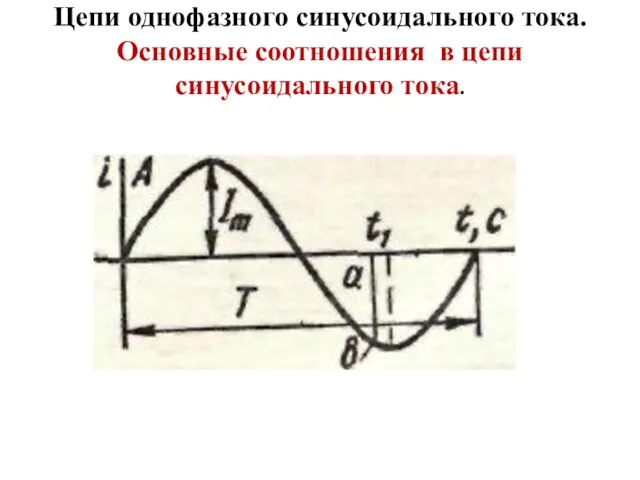
- 23. Цепи однофазного синусоидального тока. Основные соотношения в цепи синусоидального тока.
- 24. f = 50 Гц, T = 0.02 c f = 1 / T Синусоидальный ток. Если
- 25. Цепи однофазного синусоидального тока. Обозначения: Мгновенные значения: i, u, e, p; Амплитудные значения: Im, Um, E
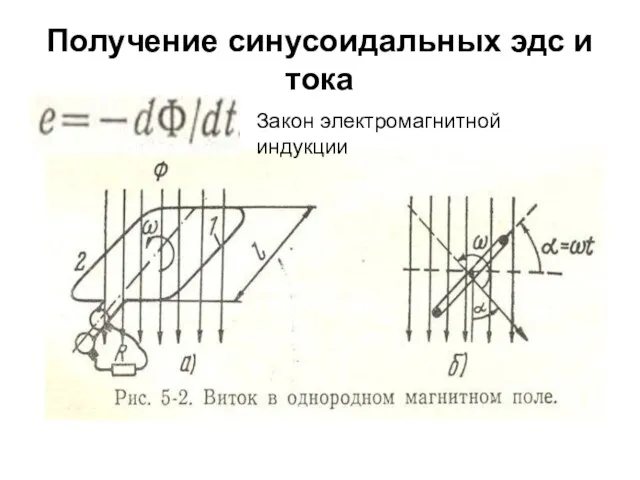
- 26. Получение синусоидальных эдс и тока В равномерное магнитное поле поместим рамку, состоящую из одного витка (рис.
- 27. Получение синусоидальных эдс и тока Закон электромагнитной индукции
- 28. Получение синусоидальных эдс и тока Преобразуем исходное выражение для наведенной эдс (е). Смотри рис.5.2
- 29. Получение синусоидальных эдс и тока Эдс витка, вращающегося в магнитном поле, изменяется во времени по синусоидальному
- 30. Вывод: Получение синусоидальных эдс и тока При всяком изменении магнитного потока через проводящий контур в этом
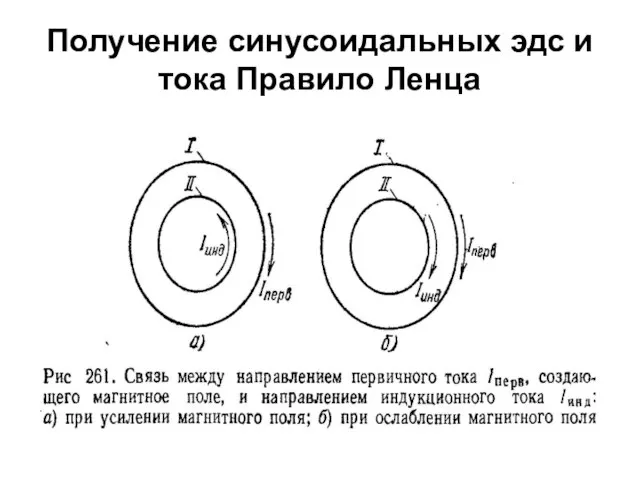
- 31. Получение синусоидальных эдс и тока Правило Ленца
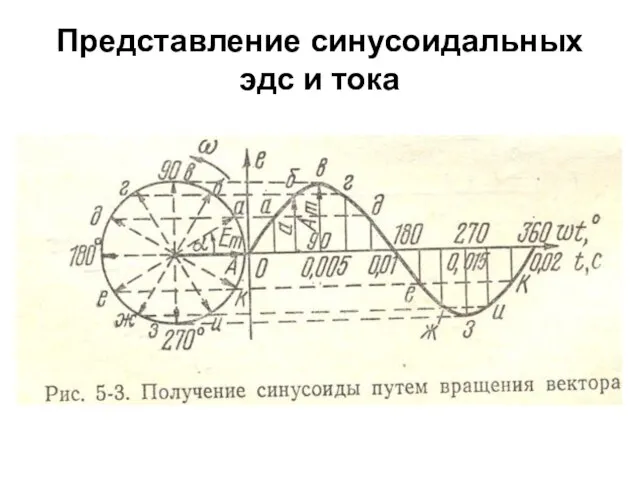
- 32. Представление синусоидальных эдс и тока Синусоидальную функцию времени можно представить: а) графиком; б) уравнением i=Im sin
- 33. Представление синусоидальных эдс и тока
- 34. Действующие значения переменного тока Действующим значением переменного тока называется такой постоянный ток, который на одинаковом сопротивлении
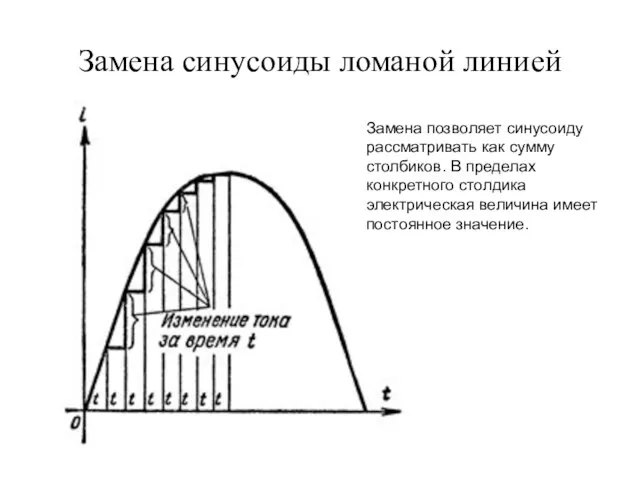
- 35. Замена синусоиды ломаной линией Замена позволяет синусоиду рассматривать как сумму столбиков. В пределах конкретного столдика электрическая
- 36. Действующее значение переменного тока для интервала времени Δt Тогда для периода Т Имеем:
- 37. Действующее значение переменного тока Формула энергии для постоянного тока С учетом того, что : Получим: где
- 38. Действующее значение переменного тока После интегрирования и упрощения получим: Здесь величины с индексом m, - амплитудные
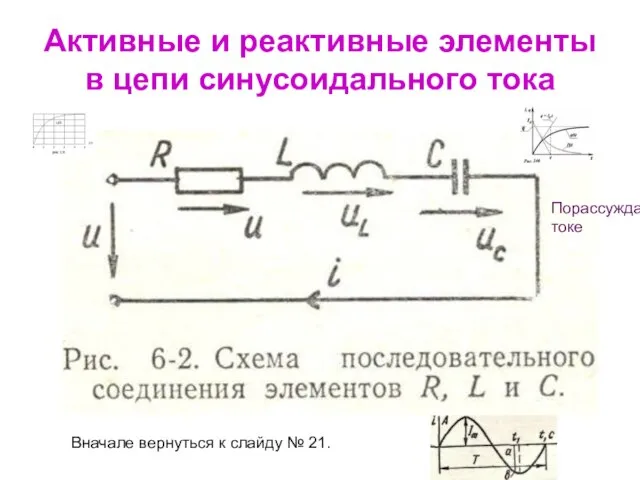
- 39. Активные и реактивные элементы в цепи синусоидального тока Вначале вернуться к слайду № 21. Порассуждать о
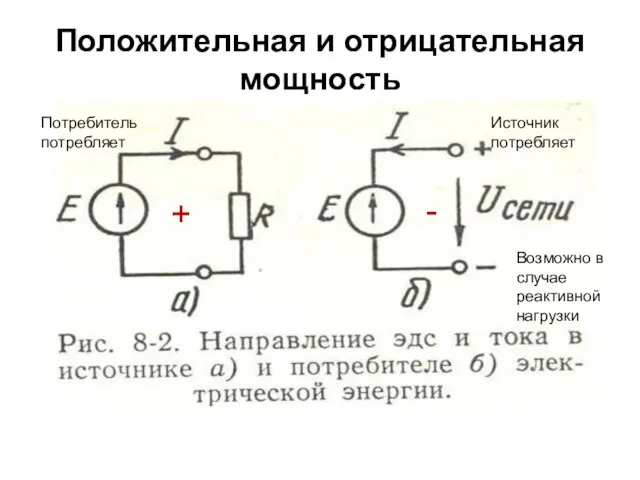
- 40. Положительная и отрицательная мощность + - Потребитель потребляет Источник потребляет Возможно в случае реактивной нагрузки
- 41. Основные формулы Активное сопротивление Когдда имеем дело с активной нагрузкой, процесс проходит аналогично цепи постоянного тока.
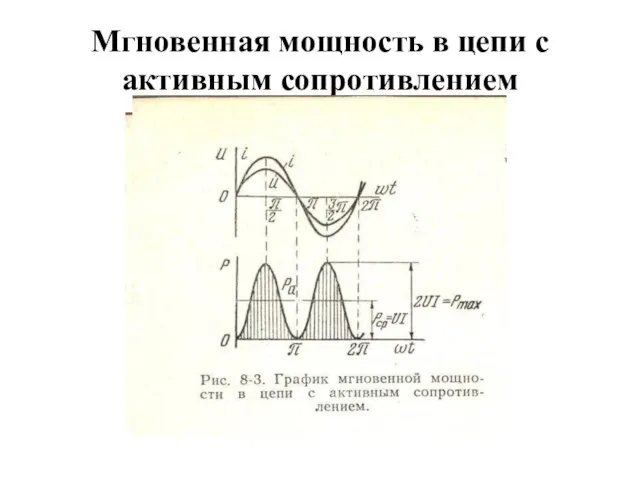
- 42. Мгновенная мощность в цепи с активным сопротивлением
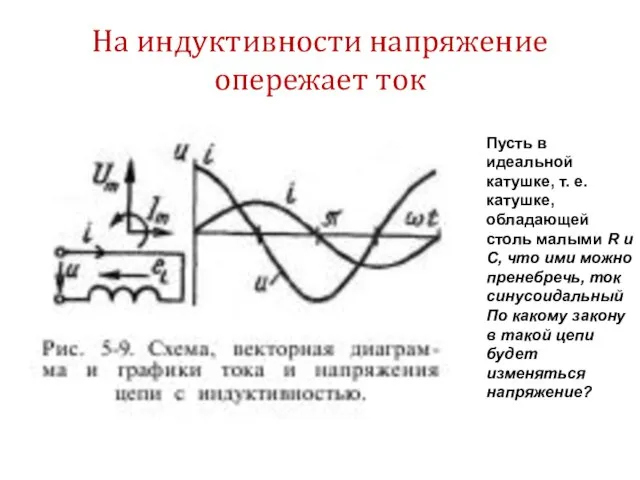
- 43. На индуктивности напряжение опережает ток Пусть в идеальной катушке, т. е. катушке, обладающей столь малыми R
- 44. На индуктивности напряжение опережает ток При изменении силы тока по гармоническому закону i=Im sinωt, ЭДС самоиндукции
- 45. Векторные диаграммы. Графики (временные диаграммы) синусоидальных функций позволяют наглядно представить их амплитуды и начальные фазы. Однако
- 46. Векторные диаграммы. Один из векторов можно расположить произвольно, но остальные векторы по отношению к нему будут
- 47. Основные формулы Индуктивность
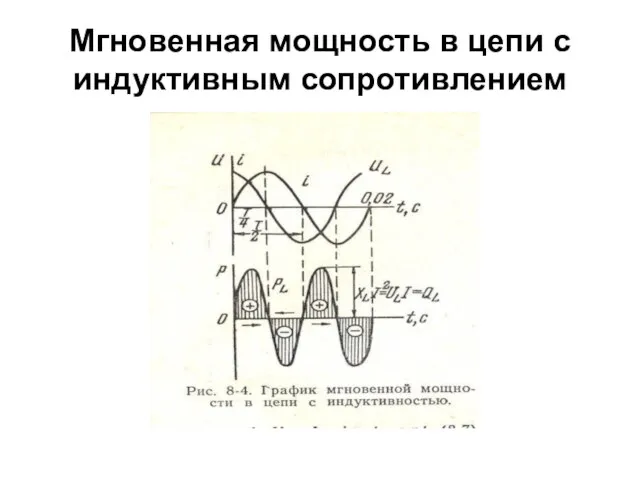
- 48. Мгновенная мощность в цепи с индуктивным сопротивлением
- 49. На емкости ток опережает напряжение i=dq / dt = Cdu/dt=Cd(Umsinωt)/dt= ωCUm sin(ωt+π/2), на индуктивности наоборот. Заряд
- 50. Основные формулы Емкость
- 51. Мгновенная мощность в цепи с емкостным сопротивлением
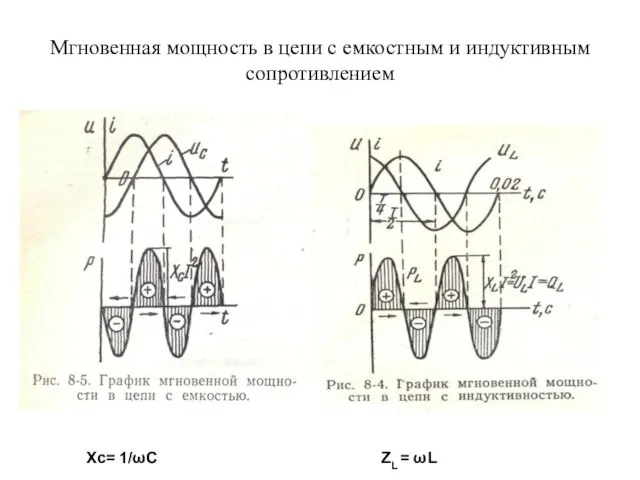
- 52. Мгновенная мощность в цепи с емкостным и индуктивным сопротивлением Xc= 1/ωC ZL = ωL
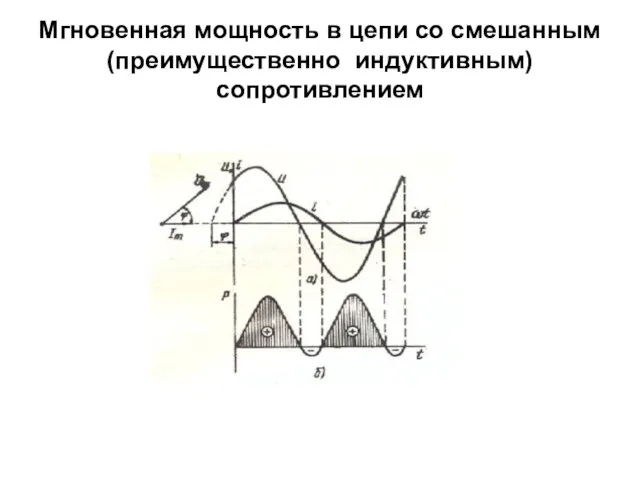
- 53. Мгновенная мощность в цепи со смешанным (преимущественно индуктивным) сопротивлением
- 54. Основные формулы цепи со смешанным (преимущественно индуктивным) сопротивлением
- 55. Основные формулы цепи со смешанным (преимущественно индуктивным) сопротивлением
- 56. Мощность в цепи переменного тока Цепь однофазного тока
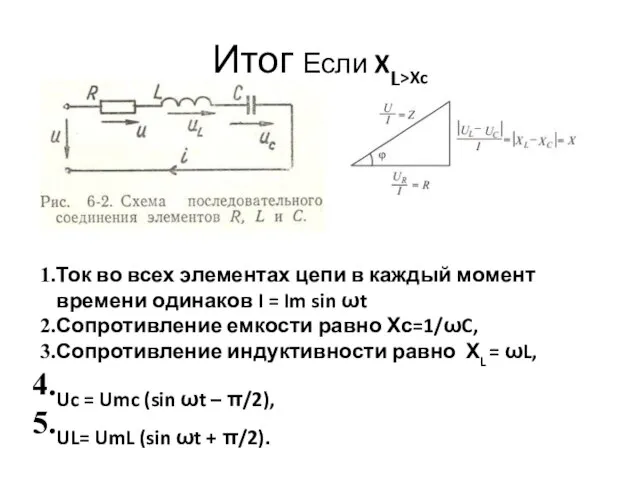
- 57. Итог Если XL>Xc Ток во всех элементах цепи в каждый момент времени одинаков I = Im
- 58. Основные формулы по теме
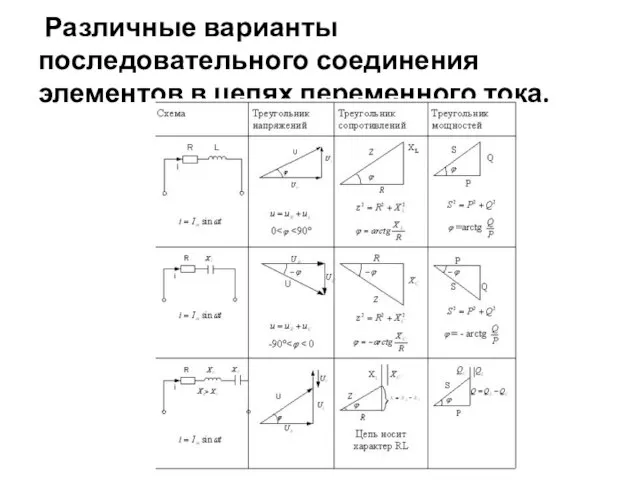
- 59. Различные варианты последовательного соединения элементов в цепях переменного тока.
- 60. Изображение комплексными числами. Для аналитического решения плоскость координат XOY заменим комплексной плоскостью (рис. 5.4). Так как
- 61. Трехфазные электрические цепи. Тема №1: Трёхфазная цепь Получение системы трёхфазных ЭДС. Способы соединения фаз трёхфазных источников
- 62. АЭС Фукусима-1 Япония до аварии.
- 63. Атомная энергетика Японии На момент начала 2011 года ядерная энергетика обеспечивала 30% потребности Японии и планировалось
- 64. Атомная энергетика Японии Новые подходы Обсуждение будущего АЭС в Японии началось с планов по закрытию всех
- 65. Разрушенный 4 блок на Чернобыльской АЭС
- 66. Трехфазные электрические цепи. Тема №1: Трёхфазная цепь Получение системы трёхфазных ЭДС. Способы соединения фаз трёхфазных источников
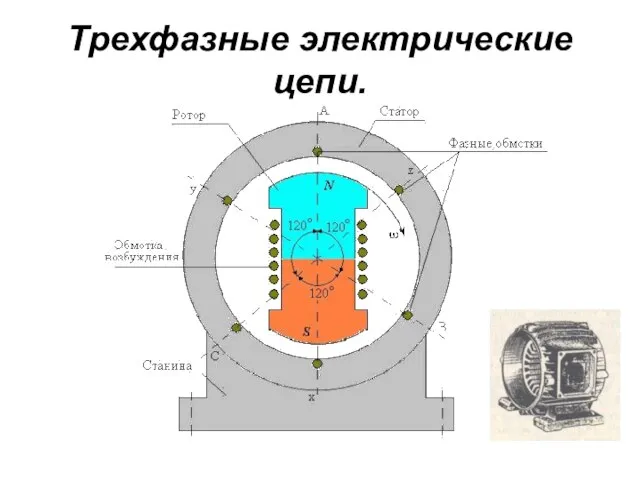
- 67. Трехфазные электрические цепи.
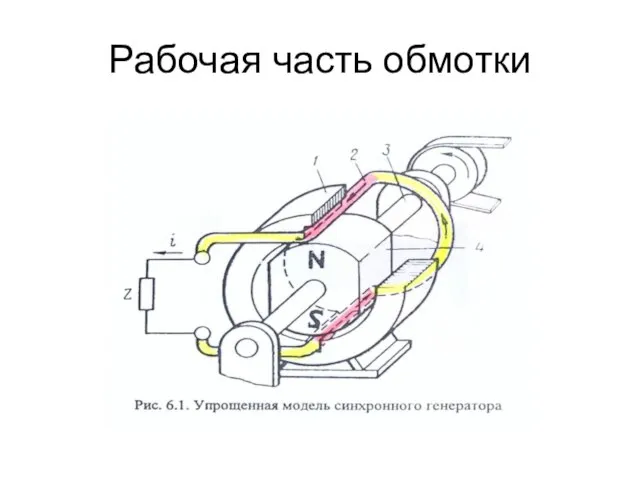
- 68. Рабочая часть обмотки
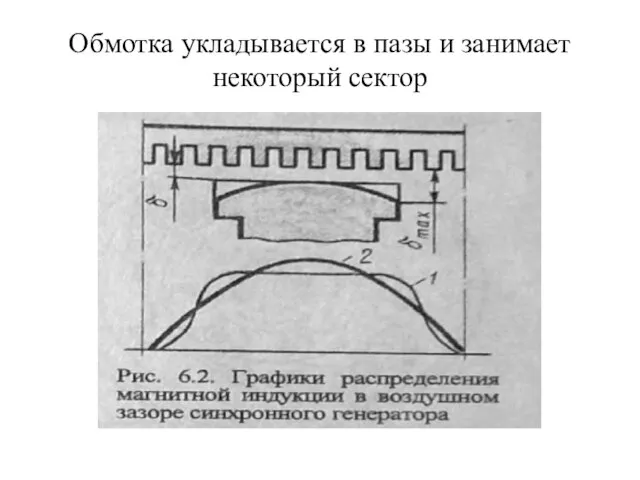
- 69. Обмотка укладывается в пазы и занимает некоторый сектор
- 70. Определения Фазные и линейные величины. Величины, относящиеся к одной фазе (рис. 10-5), получили название фазных: фазные
- 71. Определения Напряжения между линейными проводами называются линейными: U a в, U в с, U с а.
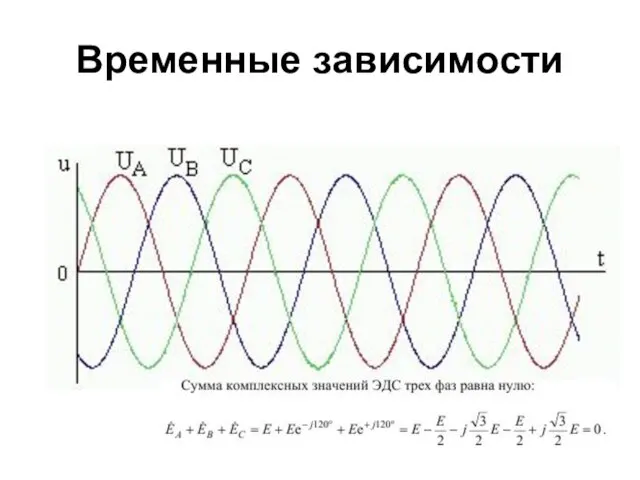
- 72. Симметричная система ЭДС Симметричная система ЭДС – это три синусоиды, сдвинутые относительно друг друга по фазе
- 73. Временные зависимости
- 74. Представление комплексными числами в показательной форме Математика для перемножения векторных величин
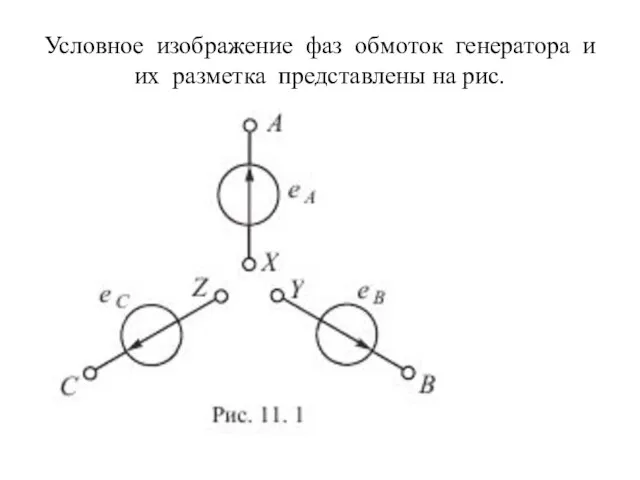
- 75. Условное изображение фаз обмоток генератора и их разметка представлены на рис.
- 76. Трехфазная система ЭДС для мгновенных значений
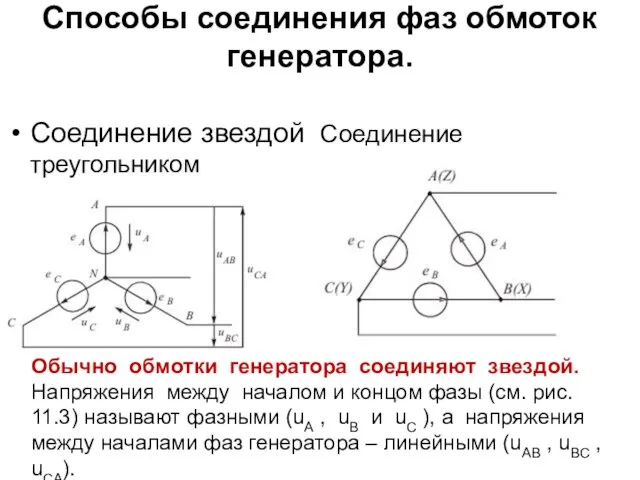
- 77. Способы соединения фаз обмоток генератора. Соединение звездой Соединение треугольником Обычно обмотки генератора соединяют звездой. Напряжения между
- 78. Соотношение между линейным и фазным напряжением при соединении источника звездой
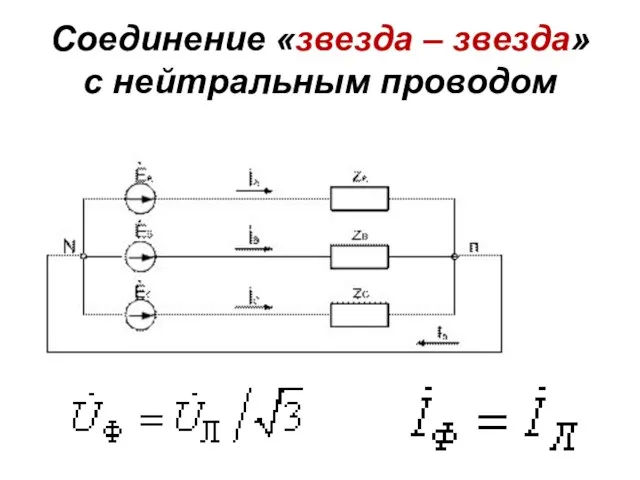
- 79. Соединение «звезда – звезда» с нейтральным проводом
- 80. Соединение звезда – звезда без нейтрального провода. Этот режим эксплуатации трехфазных цепей на практике не желателен.
- 81. звезда – звезда Несимметричный режим без нулевого провода Линейные напряжения Uab, Ubc, Uca остаются неизменными при
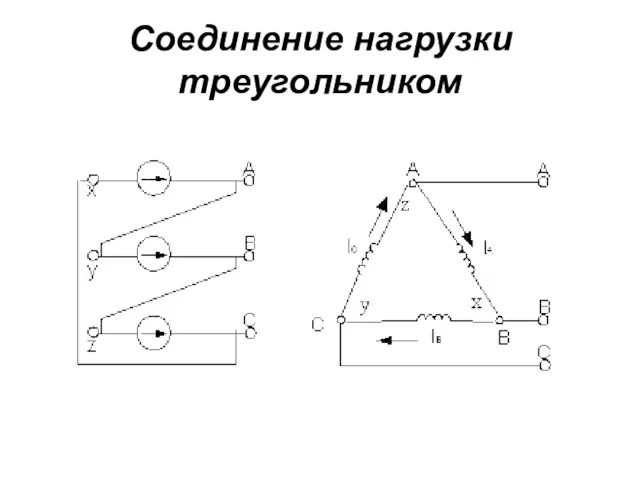
- 82. Соединение нагрузки треугольником
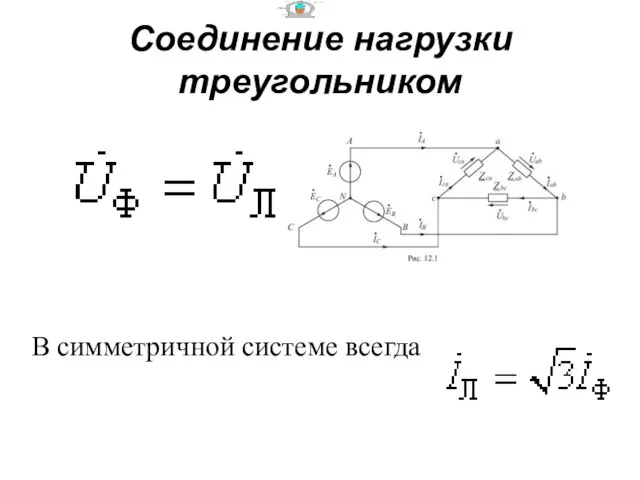
- 83. Соединение нагрузки треугольником В симметричной системе всегда
- 84. В несимметричной системе фазные токи
- 85. В несимметричной системе Линейные токи
- 86. Для симметричной нагрузки В трехфазных цепях различают те же мощности, что и в однофазных: мгновенную р,
- 87. Реактивная мощность фазы
- 88. Тема 2. Трёхфазная цепь (продолжение) Вращающееся магнитное поле. Принцип действия асинхронных двигателей.
- 89. Основные формулы по теме Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи
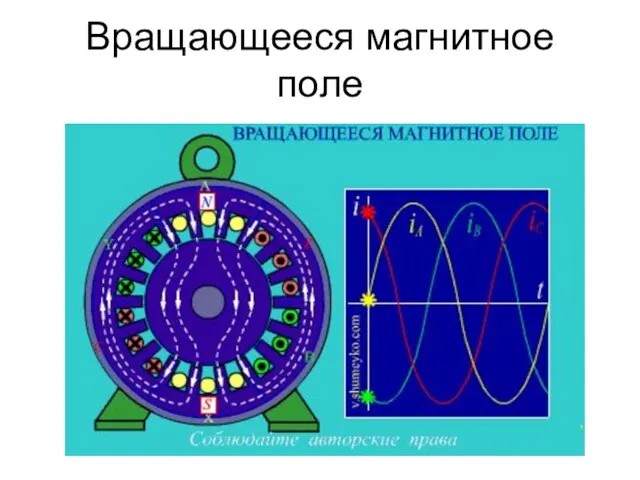
- 90. Вращающееся магнитное поле
- 91. Вращающееся магнитное поле Касаткин
- 92. Вращающееся магнитное поле
- 93. Вращающееся магнитное поле
- 94. Магнитная индукция поля статора Вывод: значение магнитной индуции постоянно и равно 1.5 Вm. Угол α, образуемый
- 95. Как изменить направление вращения магнитного поля статора Чтобы изменить направление вращения магнитного поля статора, достаточно изменить
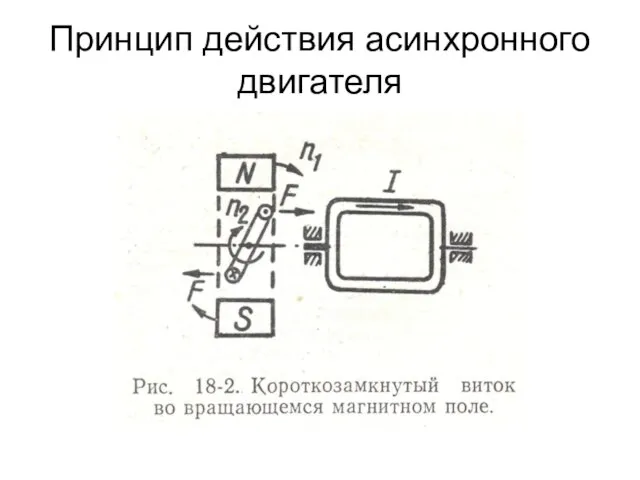
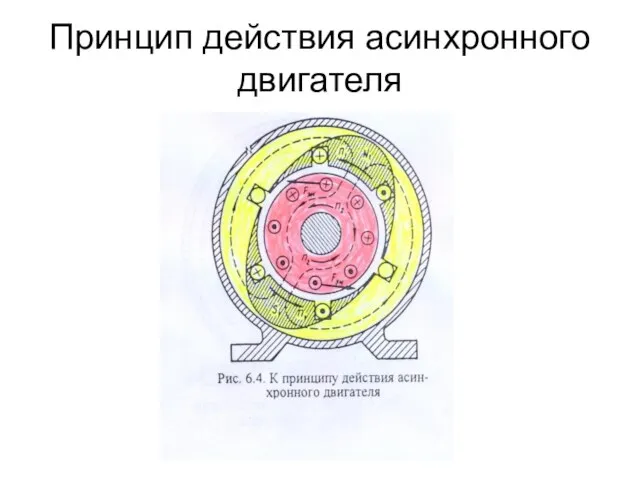
- 96. Принцип действия асинхронного двигателя
- 97. Принцип действия асинхронного двигателя Расположим во вращающемся магнитном поле укрепленный на оси замкнутый виток провода (рис.
- 98. Принцип действия асинхронного двигателя
- 100. Скачать презентацию
































































 СИЛИКОНОВАЯ ПОСУДА
СИЛИКОНОВАЯ ПОСУДА МЫ ЕДЕМ НА МОРЕ (часть 1)
МЫ ЕДЕМ НА МОРЕ (часть 1) Часы – величайшее изобретение человечества
Часы – величайшее изобретение человечества Подобные фигуры
Подобные фигуры История развития сельскохозяйственного права
История развития сельскохозяйственного права Криптосистемы с открытым ключем
Криптосистемы с открытым ключем Городская неделя музыки
Городская неделя музыки Технология выкраски архитектурного фасада
Технология выкраски архитектурного фасада Инвестиционное предложение по вовлечению в хозяйственный оборот производственной базы ОАО Лепельпромшвеймебель
Инвестиционное предложение по вовлечению в хозяйственный оборот производственной базы ОАО Лепельпромшвеймебель Внеурочная деятельность
Внеурочная деятельность Transthoracic Echocardiography
Transthoracic Echocardiography  Презентация на тему Ботаника наука о растениях 6 класс
Презентация на тему Ботаника наука о растениях 6 класс  Привитие этнокультурных ценностей через урок и внеклассные мероприятия
Привитие этнокультурных ценностей через урок и внеклассные мероприятия Презентация на тему Астероиды
Презентация на тему Астероиды  Лекция 1-3
Лекция 1-3 Христианская милость и милостыня
Христианская милость и милостыня Типы речи. Стили речи. Описание животного
Типы речи. Стили речи. Описание животного Речевая творческая минутка.
Речевая творческая минутка. Презентация на тему Жостово роспись по металлу (5 класс)
Презентация на тему Жостово роспись по металлу (5 класс) Забота государства о сохранении духовных ценностей
Забота государства о сохранении духовных ценностей Проблемы периодизации всемирной истории
Проблемы периодизации всемирной истории Жизнь и творчество И.С.Тургенева 1818 -1883
Жизнь и творчество И.С.Тургенева 1818 -1883 Литературный поединок
Литературный поединок 701661
701661 Теория государства и права – 1. Обычаи, мораль, право, нормы, правоотношения и их структура, правонарушения и их состав
Теория государства и права – 1. Обычаи, мораль, право, нормы, правоотношения и их структура, правонарушения и их состав Тиристоры
Тиристоры Законодательное собрание Ульяновской области
Законодательное собрание Ульяновской области Машинное обучение: качество
Машинное обучение: качество