Содержание
- 2. Умеете ли Вы считать? Каждый, конечно скажет: «Да!» Это очень важные умения, так как вычислительные навыки
- 3. Хорошо ли Вы считаете? Об умении считать можно судить: - по умению производить устные и письменные
- 4. Проблема исследования Много ошибок при выполнении вычислений, сложности при устном счёте.
- 5. Основополагающий вопрос Как за короткое время научиться быстро считать, если ты обыкновенный школьник, а не вундеркинд?
- 6. Гипотеза Существуют специальные способы выполнения действий, которые позволяют свести вычисления к устным, рассчитанные на ум «обычного»
- 7. Цель проекта Найти и освоить приёмы, позволяющие выполнить действия с числами быстро (устно) и безошибочно. Создать
- 8. Творческое название исследовательского проекта БЫСТРЫЙ СЧЁТ БЕЗ КАЛЬКУЛЯТОРА
- 9. 1) Общие приемы устного счета. 2) Специальные приемы устного счета: а) прием округления; б) умножение и
- 10. Общие приемы устного счета разложение каждого слагаемого на разряды; использование переместительного и сочетательного свойства сложения (умножения);
- 11. Например: 673 + 243 = 673 + 200 + 40 + 3 = 916 864 -
- 12. Запомни! 5 · 2 = 10 25 · 4 = 100 125 · 8 = 1000
- 13. Например: 38 · 4 · 25 = 38 · 100 = 3800 125 · 79 ·
- 14. Распределительное свойство при умножении и делении (а + b)· с = а · с + b
- 15. Например: 198 · 4=(200–2) ·4=200 ·4 – 2·4=800 – 8=792 91 · 8 = (90 +
- 16. Прием округления 1. Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо
- 17. 3. Если вычитаемое увеличить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность
- 18. Умножение и деление на 4, 8, 16,… Чтобы число умножить на 4, его дважды удваивают. 213·
- 19. Умножение и деление на 5, 25, 125 Чтобы число умножить на 5, нужно умножить его на
- 20. Например: 138 · 5 = (138 · 10) : 2 = 1380 : 2 = 690
- 21. Умножение на 1,5 Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину. 24
- 22. Возведение в квадрат числа, оканчивающегося цифрой 5 Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например,
- 23. Например:
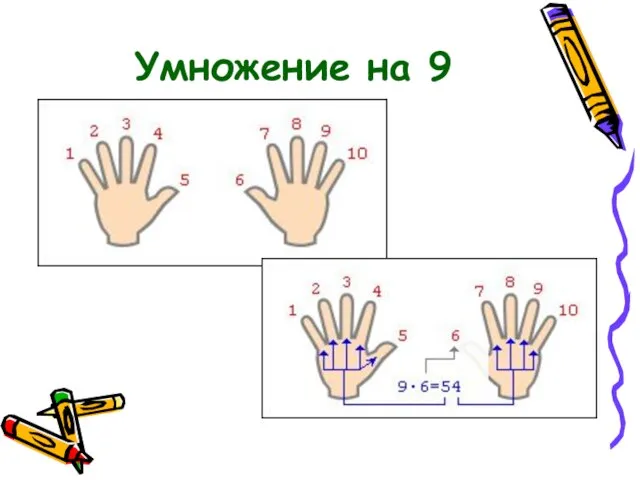
- 24. Умножение на 9, 99, 999,… Чтобы умножить число на 9, к нему приписывают 0 и отнимают
- 25. Например: 241 · 9 = 2410 – 241 = 2169 23 ∙ 99 = 2300 –
- 26. Умножение на 9
- 27. Умножение на 11 Чтобы умножить число на 11, к нему приписывают 0 и прибавляют исходное число.
- 28. Умножение на 11 Чтобы умножить на 11 двузначное число, сумма цифр которого ≥ 10, надо мысленно
- 29. Умножение на 101, 1001 Чтобы умножить число на 101, нужно приписать к нему два нуля и
- 30. Заключение Действительно, существуют специальные способы выполнения действий, которые позволяют свести вычисления к устным, быстрым, не требующие
- 32. Скачать презентацию





















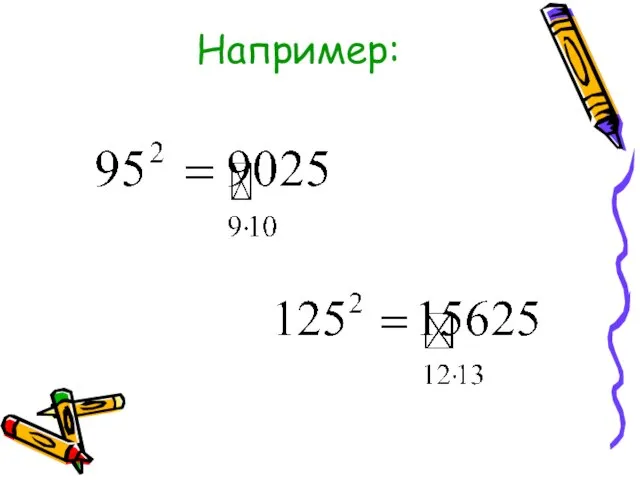






 Talk for a minute
Talk for a minute Литературная игра для младших школьников по произведениям Н.Н.Носова «Затейники и фантазёры»
Литературная игра для младших школьников по произведениям Н.Н.Носова «Затейники и фантазёры» L`italiano è facile
L`italiano è facile Коммуникации. Техника 3-х касаний
Коммуникации. Техника 3-х касаний Муниципальное образовательное учреждение "Ковылкинская средняя общеобразовательная школа № 1"
Муниципальное образовательное учреждение "Ковылкинская средняя общеобразовательная школа № 1" Грант 2013г
Грант 2013г Тема урока: «Бунташный век».
Тема урока: «Бунташный век». History & Mystery of the English language
History & Mystery of the English language Внутренняя среда организма. Кровеносная система
Внутренняя среда организма. Кровеносная система Современные средства поражений
Современные средства поражений ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯШКОЛА
ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯШКОЛА lecture_1
lecture_1 Тукай начал изучать русский язык
Тукай начал изучать русский язык История праздника Новый Год
История праздника Новый Год Проект: видеоблог
Проект: видеоблог Расчет теплоусвоения внутренней поверхности полов
Расчет теплоусвоения внутренней поверхности полов ЭФФЕКТ КАЗИМИРА: ОТ НАНОТЕХНОЛОГИЙ ДО ФИЗИКИ ВСЕЛЕННОЙ
ЭФФЕКТ КАЗИМИРА: ОТ НАНОТЕХНОЛОГИЙ ДО ФИЗИКИ ВСЕЛЕННОЙ Цифровые права
Цифровые права Сетевой маркетинг
Сетевой маркетинг культура и достопримечательности Греции
культура и достопримечательности Греции Мектеп бітірушілердің психологиялық-физиологиялық жағдайын ескере отырып қобалжу деңгейін төмендету
Мектеп бітірушілердің психологиялық-физиологиялық жағдайын ескере отырып қобалжу деңгейін төмендету Решение текстовых задач. Закрепление пройденного
Решение текстовых задач. Закрепление пройденного Традиционная реклама
Традиционная реклама Saint Patricks day
Saint Patricks day КОМПЬЮТЕРНАЯ ДОЛИНА
КОМПЬЮТЕРНАЯ ДОЛИНА Литературная игра по творчеству А.С. Пушкина
Литературная игра по творчеству А.С. Пушкина Презентация на тему Семейство Губоцветные
Презентация на тему Семейство Губоцветные ФИЗИЧЕСКАЯ КУЛЬТУРА
ФИЗИЧЕСКАЯ КУЛЬТУРА