Цели, методы и ограничения формализации требований к программам

ПЛАН
Введение
Сложность программных систем
Ошибки в ПО и их последствия
Формальные методы
Что это такое
Какие формализмы используются
Формальные методы на практике
Формализация требований
Отличия от «классических» формальных методов?
Примеры
Ограничения формализации требований
Заключение

SOFTWARE CRISIS
Конференция NATO 1968
Software сложнее hardware
Программная инженерия

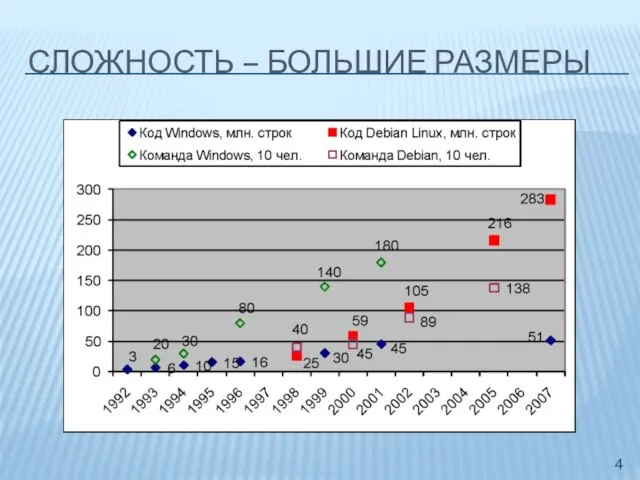
СЛОЖНОСТЬ – БОЛЬШИЕ РАЗМЕРЫ

СЛОЖНОСТЬ ИНТЕРФЕЙСА

СЛОЖНОСТЬ – МНОГО КОМПОНЕНТОВ

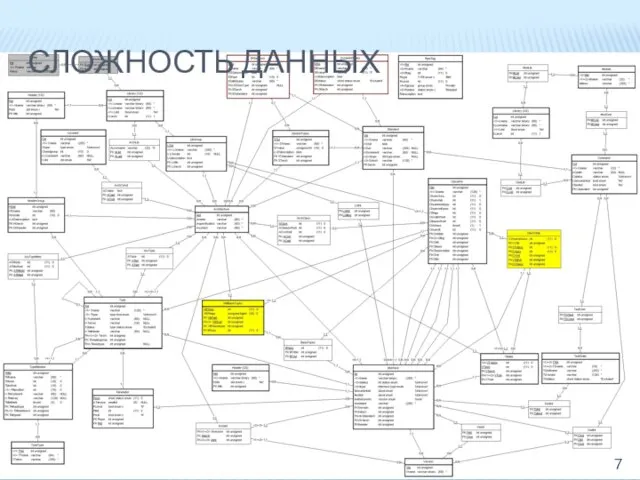
СЛОЖНОСТЬ ДАННЫХ

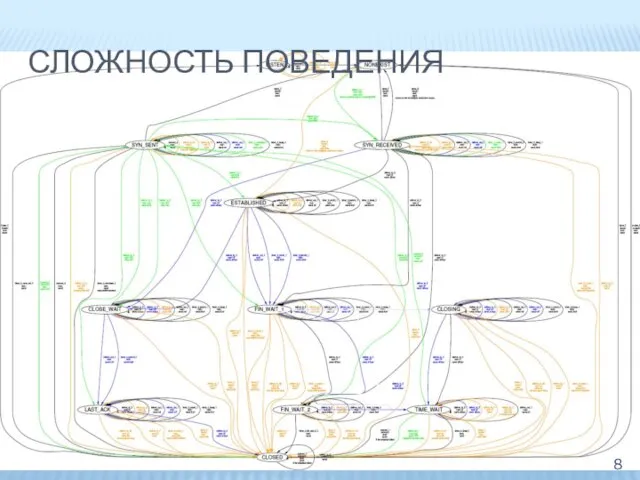
СЛОЖНОСТЬ ПОВЕДЕНИЯ

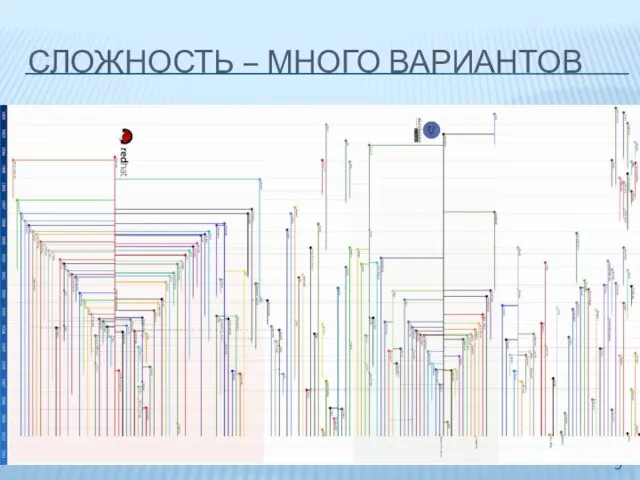
СЛОЖНОСТЬ – МНОГО ВАРИАНТОВ

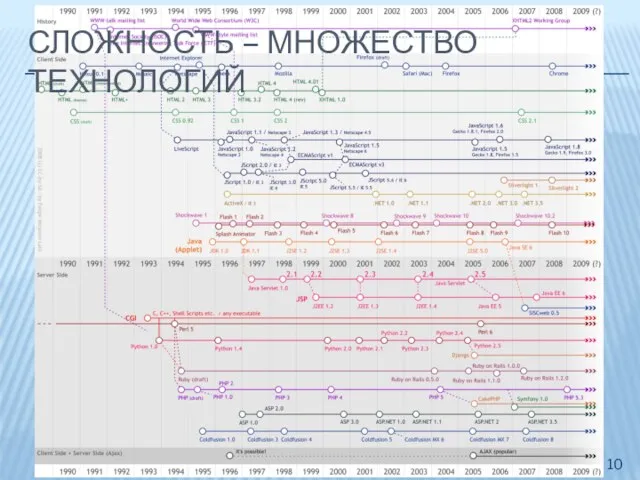
СЛОЖНОСТЬ – МНОЖЕСТВО ТЕХНОЛОГИЙ

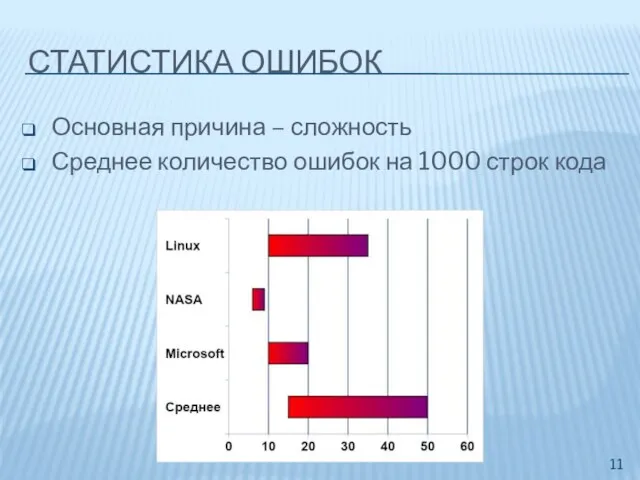
СТАТИСТИКА ОШИБОК
Основная причина – сложность
Среднее количество ошибок на 1000 строк кода

РИСКИ, СВЯЗАННЫЕ С ОШИБКАМИ
Космические аппараты
Mariner I (1962)
Фобос-1 (1988)
Ariane 5 (1996)
Mars Climate Orbiter (1999)
Инфраструктура
AT&T long distance network crash (1990)
Northeast Blackout (2003)
OpenSSL rnd in Debian (2006-8)
Heathrow Airport Terminal 5 baggage system (2008)
Автомобили
Toyota Prius (2005, 2010)
Медицинское оборудование
Therac-25 (1985-7)
Medtronic Maximo (2008)
Авионика и военное оборудование
Lockheed F-117 (1982)
MIM-104 Patriot (1991)
Chinook ZD576 (1994)
USS Yorktown (1997)
F-22 Raptor (2007)
Потери индустрии США в 2001 году – 60 G$

ЧТО ДЕЛАТЬ?
Не делать ошибок
Невозможно из-за сложности
Предотвращение ошибок
Тщательный анализ требований и возможных решений
Изоляция компонентов
Повышение уровня абстракции языков
Устранение error-prone конструкций
Стандартизация и документирование
языков, протоколов и библиотек
Выявление ошибок
Верификация и валидация
Исправление ошибок

ВОЗМОЖНОЕ РЕШЕНИЕ
Программные системы – одни из самых сложных искусственных систем
Нужны методы построения программного обеспечения с заданными свойствами
Формальные методы
Формализация требований
Наиболее детальный и строгий их анализ
Формализация проектных решений
Формальный анализ и верификация свойств ПО

ИСТОКИ ФОРМАЛЬНЫХ МЕТОДОВ
Формальные языки [N. Chomsky 1956]
BNF и описание языков FORTRAN,
ALGOL60 [J. Backus 1957, P. Naur 1960]
Атрибутные грамматики [D. Knuth, 1968]
Описание PL/I [IBM Vienna, 1968]
Формальная верификация программ
[R. Floyd 1967, C. A. R. Hoare 1969]
Формальная разработка компиляторов
Венский метод (VDM)
[D. Bjørner, C. Jones, 1972]
Европейский компилятор Ada [1984]

«КЛАССИЧЕСКИЙ» ПРОЦЕСС РАЗРАБОТКИ
Формализуем постановку задачи
(требования к ПО)
Строим проектные решения
(возможно, в несколько шагов)
Доказанно корректными трансформациями
(корректность по построению, correctness by construction)
Строим решение независимо и доказываем, что оно соответствует требованиям или решению предыдущего шага
(уточнение, refinement)
Преобразуем полученное решение в код

СПОСОБЫ ОПРЕДЕЛЕНИЯ СЕМАНТИКИ
Денотационная семантика
Программы – функции, задаваемые явно
На основе множеств и отношений
На основе λ-исчисления и его расширений
Аксиоматическая семантика
Программы – объекты, удовлетворяющие аксиомам
Функции или отношения, задаваемые пред- и постусловиями
Алгебраические системы аксиом
Аксиомы временных логик
Операционная семантика
Программы – описания действий (простой) виртуальной машины

ИСПОЛЬЗУЕМЫЕ ФОРМАЛИЗМЫ
Логико-алгебраические
Различные логики
Предикаты, теории типов, временные, модальные, …
Различные алгебраические структуры
Исполнимые
Различные автоматы
FSM, LTS, расширенные, взаимодействующие, иерархические, временные, сети Петри, Statecharts, …
Гибридные
LTS ~ Алгебры процессов
Модели стандартных термов
Abstract State Machines
Программные контракты с состоянием

ПРИМЕР I – МАШИННЫЕ ЦЕЛЫЕ ЧИСЛА
Как реализовать целые числа в компьютере?
Образец – обычные целые числа Z
Конечное множество – 32 бита для хранения
Что точно нужно?
Операции +, –, * – алгебраическое кольцо
≤ 232 элементов
Действия над 0, 1, 2, -1, -2, … дают нужные результаты

ПРИМЕР I – ФОРМАЛЬНАЯ МОДЕЛЬ
Z/232Z
Кольцо вычетов по модулю 232
{[0], [1], [2], …, [232-3], [232-2], [232-1]}
Беззнаковые числа
Нет отрицательных чисел
{[-231], [-231+1], …, [-2], [-1], [0], [1], [2], [3], …, [231-1]}
Представление
Двоичная система
Дополнительный код для отрицательных чисел
[2]*[232-1] = [232-2]
[2]*[231-1] = [-2]
[17] = 00000000000000000000000000010001
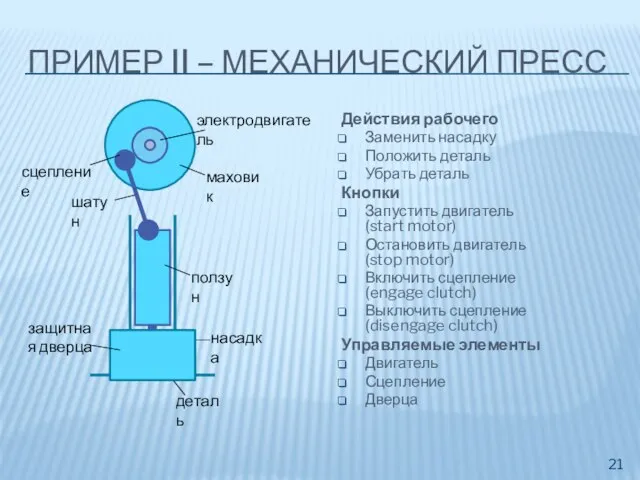
[-17] = 11111111111111111111111111101111

ПРИМЕР II – МЕХАНИЧЕСКИЙ ПРЕСС
электродвигатель
сцепление
шатун
ползун
насадка
деталь
защитная дверца
Действия рабочего
Заменить насадку
Положить деталь
Убрать деталь
Кнопки
Запустить двигатель
(start motor)
Остановить двигатель
(stop motor)
Включить сцепление
(engage clutch)
Выключить сцепление
(disengage clutch)
Управляемые элементы
Двигатель
Сцепление
Дверца
маховик

ПРИМЕР II – ПРАВИЛА БЕЗОПАСНОСТИ
Дверца должна перекрывать доступ к работающему прессу
При включении сцепления с работающим двигателем дверца должна быть закрыта
При включении двигателя с включенным сцеплением дверца должна быть закрыта
Дверца открывается только если либо двигатель не работает, либо сцепление выключено

ПРИМЕР II – УПРОЩЕНИЕ
Поскольку выключение двигателя выключает весь пресс (обычно), трудно контролировать включено ли сцепление при выключенном двигателе
Запретим эту ситуацию!
Дополнительные ограничения
Сцепление можно включать лишь при работающем двигателе
Нельзя выключить двигатель при включенном сцеплении

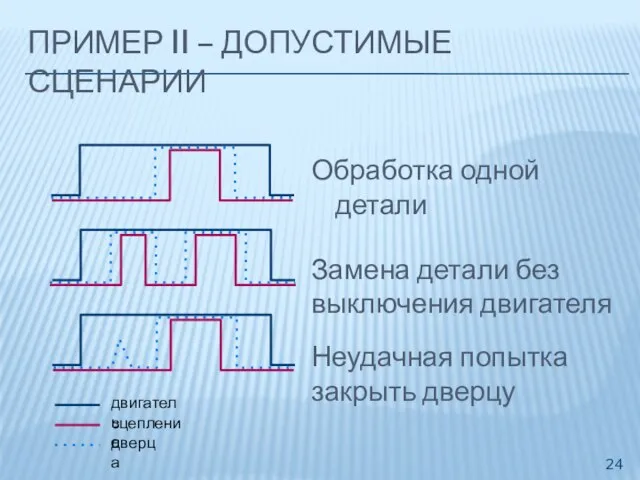
ПРИМЕР II – ДОПУСТИМЫЕ СЦЕНАРИИ
Обработка одной детали
Замена детали без выключения двигателя
Неудачная попытка закрыть дверцу
двигатель
сцепление
дверца

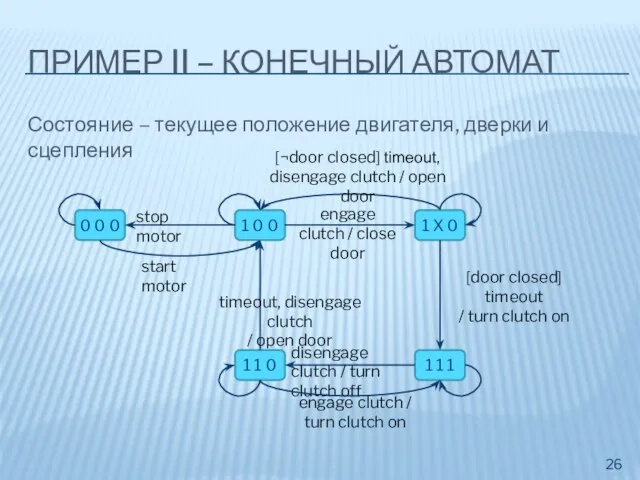
ПРИМЕР II - ТРЕБОВАНИЯ
[clutch engaged] ⇒ [door closed]
[door closed] ⇒ [motor working]
¬[motor working] ∧ [start motor] ⇒ X [motor working]
¬[door closed] ∧ [motor working] ∧ [stop motor]
⇒ X ¬[motor working]
[door closed] ⇒ ¬[stop motor]
¬[motor working] ⇒ ¬[engage clutch]
¬[door closed] ∧ [motor working] ∧ [engage clutch]
⇒ X [door closing]
[door closing] ⇒ X ¬[door closing]
[door closed] ∧ ¬[disengage clutch] ⇒ X [clutch engaged]
[door closed] ∧ [disengage clutch]
⇒ X ¬[clutch engaged] ∧ X ¬[door closed]

ПРИМЕР II – КОНЕЧНЫЙ АВТОМАТ
Состояние – текущее положение двигателя, дверки и сцепления
0 0 0
1 0 0
start motor
1 1 0
[door closed] timeout
/ turn clutch on
1 1 1
engage clutch / close door
stop motor
disengage clutch / turn clutch off
1 X 0
[¬door closed] timeout, disengage clutch / open door
timeout, disengage clutch
/ open door
engage clutch / turn clutch on

ПРИМЕР III – СПИСОК
Абстрактный тип данных List
– список объектов типа E
Операции
empty : List
insert : List
×N×E → List
size : List
→ N remove : List
×N → L
get : List
×N → E
Аксиомы
empty.size() = 0
[0≤i≤X.size()] X.insert(i, e).size() = X.size() + 1
[0≤i
[0≤i≤X.size()] X.insert(i, e).get(i) = e
[0
[0≤i
[0≤i≤X.size()] X.insert(i, e).remove(i) ≡ X
[0
[0≤i≤X.size() ∧ i
[0≤i≤X.size() ∧ 0≤j≤i] X.insert(i, e1).insert(j, e2) ≡ X.insert(j, e2).insert(i+1, e1)
[0

ПРИМЕР IV – ПОИСК ЭЛЕМЕНТА В СПИСКЕ
В этом примере список – из Лисп
List
≡ nil
| cons (E, List
)
Исчисление индуктивных конструкций
Позволяет задавать типы при помощи индуктивных конструкторов
∀l : List
l = nil
+ ∃e : E ∃m : List
l = cons(e, m)
∀e : E ∀l : List
nil
≠ cons(e, l)
∀P : List
→ Bool P(nil
) ∧ [∀e : E ∀l : List
P(l) ⇒ P(cons(e, l))] ⇒ ∀l : List
P(l)
Определения также индуктивны
contains : List
×E → Bool ≡
contains(nil
, e) ≡ false
| contains(cons(e, l), f) ≡ (e=f) ? true : contains(l, f)

ПРИМЕР IV – СПЕЦИФИКАЦИЯ
Результат поиска элемента, удовлетворяющего P : E → Bool
res(l, P) ≡ {e : E | contains(l, e) ∧ P(e)}
+ {∀x:E contains(l, x) ⇒ ¬P(x)}
Можно извлечь программу из спецификации с помощью соответствия Карри-Ховарда (Curry-Howard)

СООТВЕТСТВИЕ КАРРИ-ХОВАРДА
В конструктивной логике или конструктивных теориях типов
Доказательство ~ Программа
Логическое выражение ~ Тип
Конъюнкция ~ Декартово произведение
Импликация ~ Функция
Разбор случаев (дизъюнкция) ~ if … then … else …
Индукция в доказательстве ~ Рекурсия в программе

ПРИМЕР IV – ИЗВЛЕЧЕНИЕ ПРОГРАММЫ
Строим доказательство res(l, P) ≡ {e : E | contains(l, e) ∧ P(e)} + {∀x:E contains(l, x) ⇒ ¬P(x)}
Тип {x : A | ϕ(x)} + {ψ} имеет два конструктора
success получается из элемент a типа A вместе с доказательством ϕ(a)
fail получается из доказательства ψ
Разбор случаев
l = null
, тогда можно доказать ∀x:E contains(l, x) ⇒ ¬P(x), т.е. получаем fail
l = cons(e, m), тогда можно проверить P(e) или использовать индуктивную гипотезу для m, т.е. получаем P(e) + res(m, P)
Таким образом, программа поиска такова
search(l, P) ≡
if (l = nil
) then fail
else let l = cons(e, m)
if(P(e)) then e
else search(m, P)

ОГРАНИЧЕНИЯ ФОРМАЛЬНЫХ МЕТОДОВ
Трансформации спецификаций в программы (correctness by construction) работают только для ограниченного набора задач
При уточнении из n шагов получается n+1 формальная модель, каждая из которых по сложности приближается к итоговой системе
Даже в простейшем случае нужно сделать модель требований, модель решения и еще саму систему – в 2-3 раза больше работы
Формальный анализ сложной системы сам сложен ⇒ в нем возможны ошибки!

ПЛЮСЫ ФОРМАЛЬНОСТИ
Требования анализируются систематично и детально
Возникает глубокое понимание задачи
Получаемое решение доказуемо корректно (если хватит сил провести доказательство)
Что же делать?

«ЛЕГКИЕ» ФОРМАЛЬНЫЕ МЕТОДЫ
Формализация требований
Сохраняем аккуратность анализа
Сохраняем бонус глубокого понимания
Формальную модель решения не строим
Избавляемся от высоких затрат
Пытаемся извлекать ее автоматически из кода или работы самой системы, чтобы верифицировать саму систему
Статический анализ
Проверка извлекаемых моделей (model checking)
Тестирование на основе моделей
В итоге тратим в ~1.5 раза больше усилий, но получаем гораздо более качественный результат
Это окупается для систем, некорректность которых стоит дорого

ТЕХНИКИ ВЕРИФИКАЦИИ
Статический анализ + проверка моделей
Тестирование на основе моделей
Инструмент анализа
do {
; ...
if(*) {
...
;
}
} while (*);
do {
b = true;
...
if(*) {
...
b = b?false:*;
}
} while (!b);
do {
b = true;
...
if(r) {
...
b = b?false:*;
}
} while (!b);
Сопоставление с моделью
do {
nPacketsOld = nPackets;
...
if(request) {
...
nPackets++;
}
} while (nPackets != nPacketsOld);

ПРИМЕР V – ALTERNATING BIT PROTOCOL
Протокол канального уровня
7-уровневая модель OSI
Физический уровень
Канальный уровень
Сетевой уровень
Транспортный уровень
Уровень представления
Сеансовый уровень
Прикладной уровень
Симплексный – передача в одну сторону
Должен гарантировать надежную доставку кадра

ПРИМЕР V – ОТПРАВИТЕЛЬ
typedef enum { frame_arrival, cksum_err, timeout } event_type;
#include "protocol.h"
void sender() {
seq_nr next_frame_to_send; /* номер следующего кадра */
frame s; /* временная переменная – кадр для передачи */
packet buffer; /* буфер для исходящего пакета */
event_type event;
next_frame_to_send = 0; /* инициализация номеров исх. кадров */
from_network_layer(&buffer); /* получаем первый пакет */
while(true) {
s.info = buffer; /* формируем кадр для передачи */
s.seq = next_frame_to_send;
to_physical_layer(&s); /* послать кадр по каналу */
start_timer(s.seq); /* таймер для подтверждения */
wait_for_event(&event); /* ожидаем события */
if(event == frame_arrival) {
from_physical_layer(&s); /* получить подтверждение */
if(s.ack == next_frame_to_send) {
from_network_layer(&buffer); /* получаем след. пакет */
inc(next_frame_to_send); /* меняем четность */
}
}
}
}

ПРИМЕР V – ПОЛУЧАТЕЛЬ
void receiver() {
seq_nr frame_expected; /* номер ожидаемого кадра */
frame r, s; /* получаемый кадр и кадр подтверждения */
event_type event;
frame_expected = 0; /* инициализация номера ожидаемого кадров */
while(true)
{
wait_for_event(&event);
if(event == frame_arrival) /* приходит какой-то кадр */
{
from_physical_layer(&r); /* получаем его с физического уровня */
if(r.seq == frame_expected) /* если ожидаем именно его */
{
to_network_layer(&r.info); /* отдаем пакет на сетевой уровень */
inc(frame_expected); /* меняем четность */
}
s.ack = previous(frame_expected); /* выставляем четность подтверждения */
to_physical_layer(&s); /* отправляем подтверждение */
}
}
}

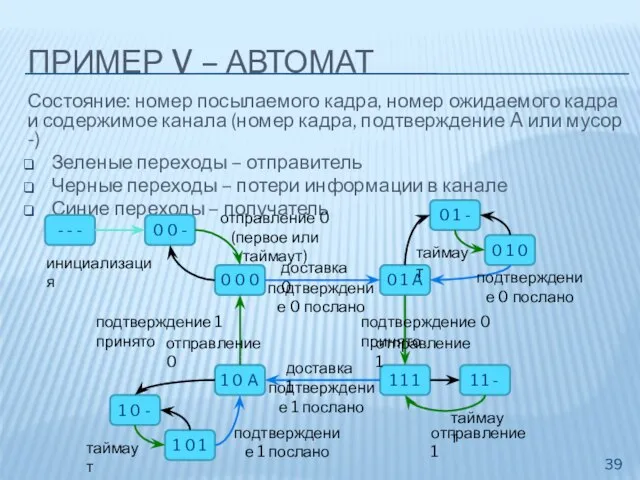
ПРИМЕР V – АВТОМАТ
Состояние: номер посылаемого кадра, номер ожидаемого кадра и содержимое канала (номер кадра, подтверждение A или мусор -)
Зеленые переходы – отправитель
Черные переходы – потери информации в канале
Синие переходы – получатель
0 0 0
0 1 A
- - -
0 0 -
1 1 1
0 1 -
0 1 0
1 1 -
1 0 A
1 0 -
1 0 1
инициализация
таймаут
таймаут
таймаут
отправление 0 (первое или таймаут)
доставка 0
доставка 1
подтверждение 0 послано
подтверждение 1 послано
подтверждение 0 принято
подтверждение 1 принято
подтверждение 0 послано
отправление 1
отправление 1
подтверждение 1 послано
отправление 0

Четные и нечетные посылаемые кадры чередуются
Четность посылаемого кадра не меняется два раза без изменения четности ожидаемого
Отсутствие тупиков
Нужна достаточно надежная сеть, чтобы не было неограниченных простоев
ПРИМЕР V – СВОЙСТВА И ОГРАНИЧЕНИЯ

ОБЛАСТЬ ПРИМЕНИМОСТИ
Где формализация требований оправдана?
Стандарты
Устоявшиеся протоколы, интерфейсы и языки
Системное ПО
Широко используемые и достаточно стабильные API (Application Programming Interface)
Иначе – огромные усилия уходят на выявление неявно подразумеваемых деталей, а потом анализ нужно начинать сначала из-за возникающих изменений

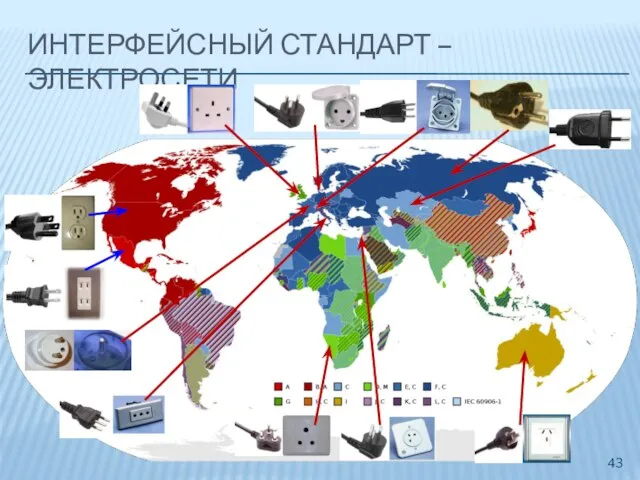
ИНТЕРФЕЙСНЫЕ СТАНДАРТЫ
Программно-аппаратные интерфейсы
x86, MIPS, ARM
Телекоммуникационные и аппаратные протоколы
Ethernet, Wi-Fi, IP, TCP, HTTP, SMTP, SOAP, Radius
API общих библиотек
POSIX, Linux Standard Base, JDK, DOM, MPI, OpenGL
Форматы файлов
XML, HTML, PDF, ODF, MP3, GIF, ZIP
Языки программирования и моделирования
C++, Java, C#, Fortran, Ada, Scheme, Verilog

ИНТЕРФЕЙСНЫЙ СТАНДАРТ – ЭЛЕКТРОСЕТИ

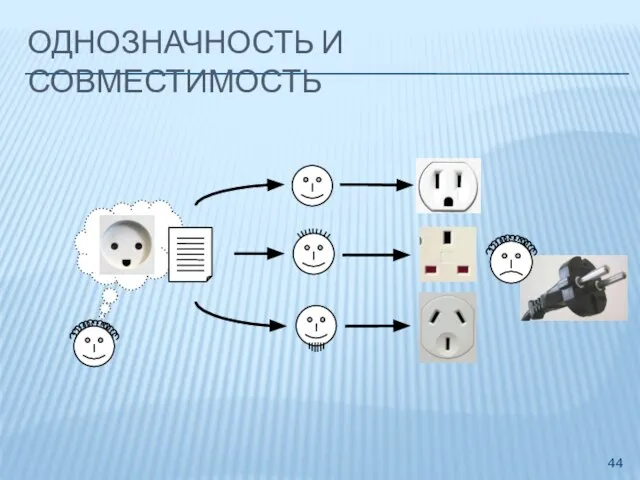
ОДНОЗНАЧНОСТЬ И СОВМЕСТИМОСТЬ

ПРИМЕР VI – ЧИСЛА С ПЛАВАЮЩЕЙ ТОЧКОЙ
Представляют вещественные числа
Бесконечное (даже несчетное) множество представляется конечным
Двоичная система счисления точно представляет лишь числа вида N/2n
Вводятся ограничения на величину и малость
Стандарт IEEE 754 [1982, 2008]

ПРИМЕР VI – ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
Нормализованные: E > 0 ∧ E < 2k –1 X = (–1)S·2(E–B)·(1+M/2(n–k–1))
Денормализованные: E = 0 X = (–1)S·2(–B+1)·(M/2(n–k–1))
Exceptional : E = 2k –1
M = 0 : +∞, –∞
M ≠ 0 : NaN
знак
k+1
n-1
0
экспонента
мантисса
0
1
1
1
1
1
1
0
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
k
n, k
S
E
M
B = 2(k–1) –1
2(–1)·1.101002 = 13/16 = 0.8125
0, -0
1/0 = +∞, (–1)/0 = –∞
0/0 = NaN
n = 32, k = 8 – float (single precision)
n = 64, k = 11 – double
n ≤ 79, k = 15 – extended double
n = 128, k = 15 – quadruple
1/2(n-k-1) = 1 ulp

ПРИМЕР VI – НЕКОТОРЫЕ ЗНАЧЕНИЯ

ПРИМЕР VI – ОПЕРАЦИИ
+, –, *, /
fma(x,y,z)=x*y+z [2008]
remainder(x,y) = x–y*n : n=round(x/y)
sqrt
Преобразования между типами с плавающей точкой ( float ↔ double, …)
Преобразования к целым типам и обратно
(Рекомендуемые) [2008]
floor, ceil, abs, ilogb, exp, log, exp10, sin, sinp, …

ПРИМЕР VI – РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Корректное округление– 4 режима
к +∞
к –∞
к 0
к ближайшему (к четному)
(опция, 2008) к ближайшему (от 0)
Флаги исключений
INVALID : некорректные аргументы (результат NaN)
DIVISION-BY-ZERO : бесконечный результат (точно ±∞)
OVERFLOW : переполнение (результат ±∞)
UNDERFLOW : слишком малый (или денорм.) результат
INEXACT : неточный результат
0

ПРИМЕР VI – ТРЕБОВАНИЯ К SIN В POSIX
NAME sin, sinf, sinl - sine function
SYNOPSIS #include
double sin(double x); float sinf(float x); long double sinl(long double x);
DESCRIPTION
These functions shall compute the sine of their argument x, measured in radians.
An application wishing to check for error situations should set errno to zero and call feclearexcept(FE_ALL_EXCEPT) before calling these functions. On return, if errno is non-zero or fetestexcept(FE_INVALID | FE_DIVBYZERO | FE_OVERFLOW | FE_UNDERFLOW) is non-zero, an error has occurred.
RETURN VALUE
Upon successful completion, these functions shall return the sine of x.
If x is NaN, a NaN shall be returned.
If x is ±0, x shall be returned.
If x is subnormal, a range error may occur and x should be returned.
If x is ±Inf, a domain error shall occur, and either a NaN (if supported), or an implementation-defined value shall be returned.
ERRORS
These functions shall fail if:
Domain Error The x argument is ±Inf. If the integer expression (math_errhandling & MATH_ERRNO) is non-zero, then errno shall be set to [EDOM]. If the integer expression (math_errhandling & MATH_ERREXCEPT) is non-zero, then the invalid floating-point exception shall be raised.
These functions may fail if:
Range Error The value of x is subnormal If the integer expression (math_errhandling & MATH_ERRNO) is non-zero, then errno shall be set to [ERANGE]. If the integer expression (math_errhandling & MATH_ERREXCEPT) is non-zero, then the underflow floating-point exception shall be raised.

ПРИМЕР VI – POSIX VERSUS IEEE 754
IEEE 1003.1 (POSIX)
63 действительных функций + 22 complex
Все флаги IEEE 754 (кроме INEXACT) для действительных функций
Выставление errno
Domain error ~ INVALID или DIVISION-BY-ZERO
Range error ~ OVERFLOW или UNDERFLOW
Для денормализованного x
f(x) = x для всех функций f(x)~x в 0 (sin, asin, sinh, expm1…)
При переполнении должно возвращаться HUGE_VAL
(точное значение HUGE_VAL не определено)
Противоречие с режимами округления
Источник несовместимости
glibc : +∞
MSVCRT : max double (1.797693134862316e+308)
Solaris libc : max float (3.402823466385289e+38)
Противоречие с режимами округления

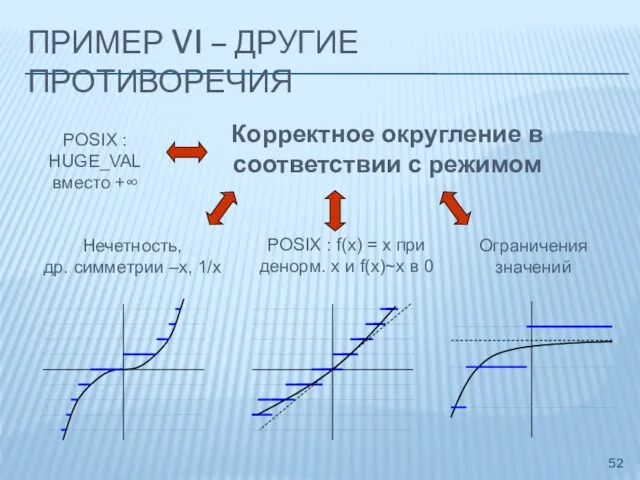
ПРИМЕР VI – ДРУГИЕ ПРОТИВОРЕЧИЯ
Ограничения значений
POSIX : f(x) = x при денорм. x и f(x)~x в 0
POSIX : HUGE_VAL
вместо +∞
Нечетность,
др. симметрии –x, 1/x
Корректное округление в соответствии с режимом

ПРИМЕР VI – КОРРЕКТНОЕ СВОЙСТВО
tan(x), atan(x) – тангенс и арктангенс
tan(atan(x)) ~ x при x → +∞
Для чисел с плавающей точкой (double)
(tan(atan(1050)) = 1.633123935319537...⋅1016
[π/2]double = 884279719003555/249
при x > tan([π/2]double) tan(atan(x)) = tan([π/2]double) ≈ 1/(π/2 - [π/2]double)
(π/2 - [π/2]double) = 6.1232339957367658…⋅10–17
π/2
atan(x)
π/2
[π/2]double

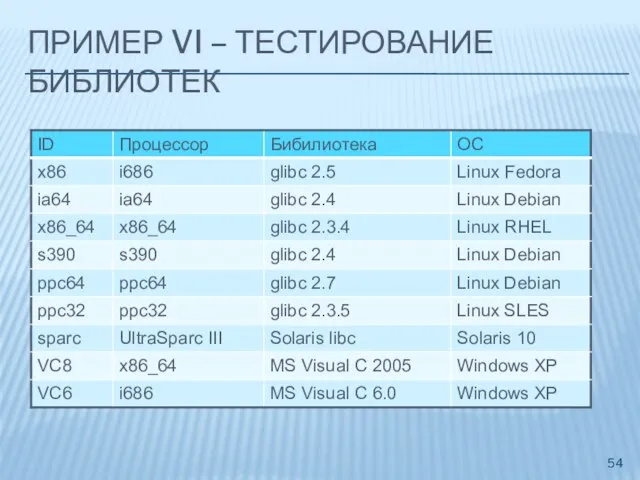
ПРИМЕР VI – ТЕСТИРОВАНИЕ БИБЛИОТЕК

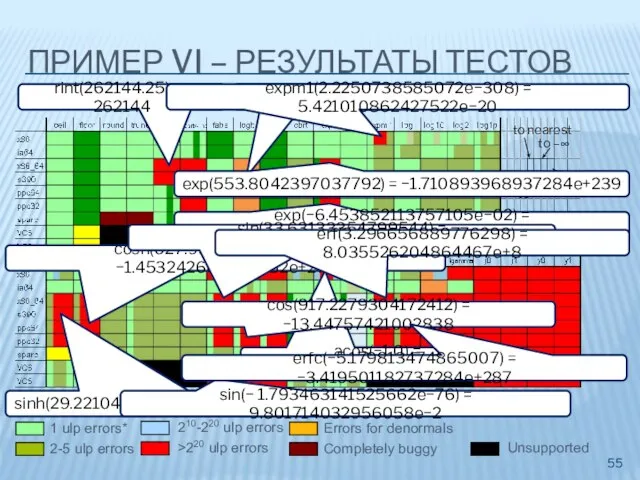
ПРИМЕР VI – РЕЗУЛЬТАТЫ ТЕСТОВ
rint(262144.25)↑ = 262144
Exact
1 ulp errors*
2-5 ulp errors
6-210 ulp errors
210-220 ulp errors
>220 ulp errors
Errors in exceptional cases
Errors for denormals
Completely buggy
Unsupported
logb(2−1074) = −1022
expm1(2.2250738585072e−308) = 5.421010862427522e−20
exp(−6.453852113757105e−02) = 2.255531908873594e+15
sinh(29.22104351584205) = −1.139998423128585e+12
cosh(627.9957549410666) = −1.453242606709252e+272
sin(33.63133354799544) = 7.99995094799809616e+22
sin(− 1.793463141525662e−76) = 9.801714032956058e−2
acos(−1.0) = −3.141592653589794
cos(917.2279304172412) = −13.44757421002838
erf(3.296656889776298) = 8.035526204864467e+8
erfc(−5.179813474865007) = −3.419501182737284e+287
to nearest
to –∞
to +∞
to 0
exp(553.8042397037792) = −1.710893968937284e+239

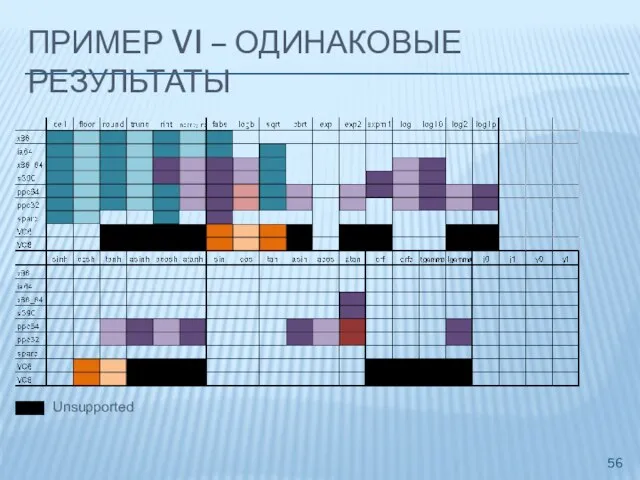
ПРИМЕР VI – ОДИНАКОВЫЕ РЕЗУЛЬТАТЫ
Unsupported

БОНУСЫ ФОРМАЛИЗАЦИИ
Представление требований в виде
математической модели
Возможности анализа
Однозначности
Непротиворечивости
Полноты
Возможности проверки (верификации)
Правила для статического анализа
Критерии корректности для тестов
Адекватность
– не гарантируется!

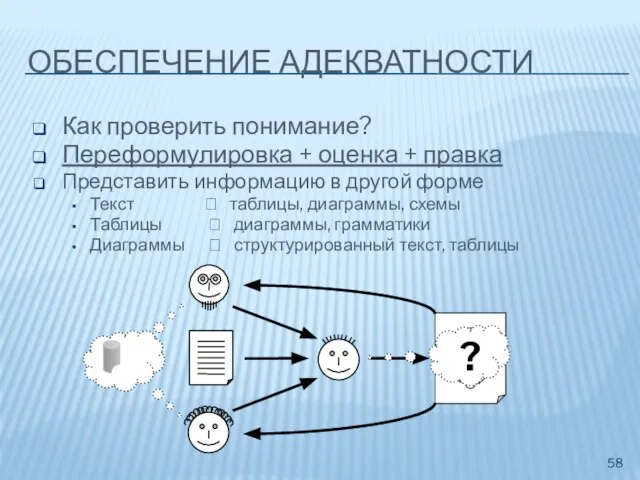
ОБЕСПЕЧЕНИЕ АДЕКВАТНОСТИ
Как проверить понимание?
Переформулировка + оценка + правка
Представить информацию в другой форме
Текст ? таблицы, диаграммы, схемы
Таблицы ? диаграммы, грамматики
Диаграммы ? структурированный текст, таблицы
?

ПРИМЕР VII – STRTOD(), POSIX
strtod – преобразование строки в число с плавающей точкой
Интерфейс
double strtod(const char *nptr, char **endptr)
Описание
Преобразует начало строки nptr в число типа double
Декомпозиция исходной строки
Начальные пробелы
Далее – то, что можно считать числом
Нераспознанные символы (начало записывается в endptr)
Преобразование распознанной части в число
Результаты
При успешной конвертации – число
Иначе
При переполнении – +HUGE_VAL или -HUGE_VAL, errno := [ERANGE] (shall)
При слишком малом результате – errno := [ERANGE] (shall)
Иначе 0, errno := [EINVAL] (may)

ПРИМЕР VII – РАЗМЕТКА ТРЕБОВАНИЙ
The expected form of the subject sequence is an optional plus or minus sign, then one of the following:
A non-empty sequence of decimal digits optionally containing a radix character, then an optional exponent part
A 0x or 0X, then a non-empty sequence of hexadecimal digits optionally containing a radix character, then an optional binary exponent part
One of INF or INFINITY, ignoring case
One of NAN or NAN(n-char-sequenceopt), ignoring case in the NAN part, where:
n-char-sequence:
digit
nondigit
n-char-sequence digit
n-char-sequence nondigit
The subject sequence is defined as the longest initial subsequence of the input string, starting with the first non-white-space character, that is of the expected form. The subject sequence contains no characters if the input string is not of the expected form.
If the subject sequence has the expected form for a floating-point number, the sequence of characters starting with the first digit or the decimal-point character (whichever occurs first) shall be interpreted as a floating constant of the C language, except that the radix character shall be used in place of a period, and that if neither an exponent part nor a radix character appears in a decimal floating-point number, or if a binary exponent part does not appear in a hexadecimal floating-point number, an exponent part of the appropriate type with value zero is assumed to follow the last digit in the string. If the subject sequence begins with a minus sign, the sequence shall be interpreted as negated. A character sequence INF or INFINITY shall be interpreted as an infinity, if representable in the return type, else as if it were a floating constant that is too large for the range of the return type. A character sequence NAN or NAN(n-char-sequenceopt) shall be interpreted as a quiet NaN, if supported in the return type, else as if it were a subject sequence part that does not have the expected form; the meaning of the n-char sequences is implementation-defined. A pointer to the final string is stored in the object pointed to by endptr, provided that endptr is not a null pointer.
If the subject sequence has the hexadecimal form and FLT_RADIX is a power of 2, the value resulting from the conversion is correctly rounded.
[CX] The radix character is defined in the program's locale (category LC_NUMERIC ). In the POSIX locale, or in a locale where the radix character is not defined, the radix character shall default to a period ( '.' ).
In other than the C [CX] or POSIX locales, other implementation-defined subject sequences may be accepted.
If the subject sequence is empty or does not have the expected form, no conversion shall be performed; the value of str is stored in the object pointed to by endptr, provided that endptr is not a null pointer.
[CX] The strtod() function shall not change the setting of errno if successful.
Since 0 is returned on error and is also a valid return on success, an application wishing to check for error situations should set errno to 0, then call strtod(), strtof(), or strtold(), then check errno.
The subject sequence is defined as the longest initial subsequence of the input string, starting with the first non-white-space character, that is of the expected form. The subject sequence contains no characters if the input string is not of the expected form.

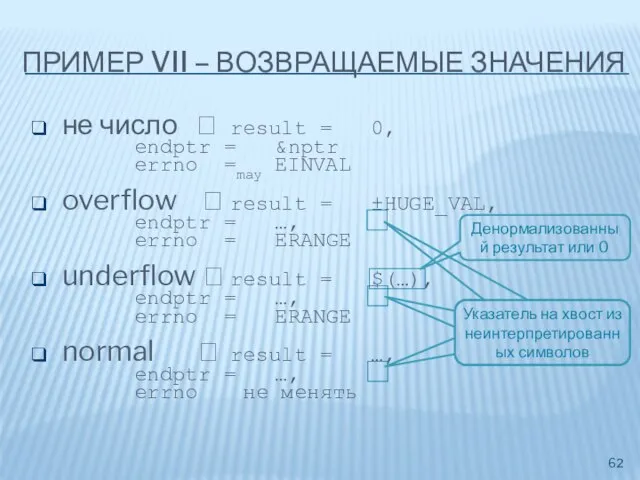
ПРИМЕР VII – РАЗБОР СТРОКИ
Radix character
( [whitespace] )*
( '+' | '-' )?
(
[digit or '.'!]+ (#'e'('+'|'-')?[digit]*)?
| #'0x'[hdigit or '.'!]+(#'p'('+'|'-')?[digit]*)?
| #'inf' ( #'inity' )?
| #'nan' [any]*
)
Exponent
Binary exponent

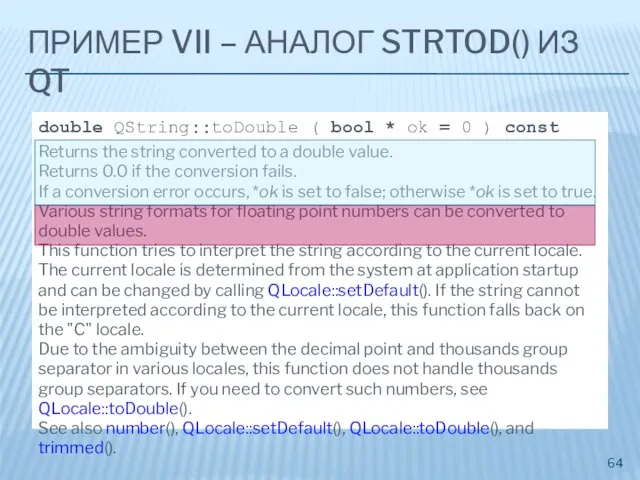
ПРИМЕР VII – ВОЗВРАЩАЕМЫЕ ЗНАЧЕНИЯ
не число ? result = 0,
endptr = &nptr
errno =may EINVAL
overflow ? result = ±HUGE_VAL,
endptr = …,
errno = ERANGE
underflow ? result = $(…),
endptr = …,
errno = ERANGE
normal ? result = …,
endptr = …,
errno не менять
Указатель на хвост из неинтерпретированных символов
Денормализованный результат или 0

ПРИМЕР VII – СПЕЦИФИКАЦИЯ STRTOD()
specification Unifloat* strtod_spec(CString* st, CString** endptr, ErrorCode* errno) {
pre { REQ("", "endpt should be not NULL", endptr != NULL); return true; }
post {
CString* model_endptr; IntT model_err = 0;
Unifloat* model_res = strtod_model(st, &model_endptr, &model_err);
round_Unifloat(strtod_spec); round_Unifloat(model_res);
if (model_err == 1) {
REQ("strtod.13", "If no conversion is performed, the value of nptr shall be stored"
"in the object pointed to by endptr", equals(st, *endptr)); }
if (*errno == SUT_EINVAL) {
REQ("strtod.15", "If no conversion could be performed, 0 shall be returned"
, isZero_Unifloat(strtod_spec)); }
if (isOverflow_Unifloat(model_res)) {
REQ("strtod.16", "If the correct value is outside the range of representable values,"
"HUGE_VAL shall be returned", isInfinity_Unifloat(strtod_spec)); }
if (isUnderflow_Unifloat(model_res)) {
REQ("strtod.17", "If the correct value would cause underflow, the smallest normalized"
"positive number shall be returned"
, (compare_Unifloat(abs_Unifloat(strtod_spec), min_Unifloat(type)) != 1)
&& (strtod_spec->sign == 1)); }
...

ПРИМЕР VII – АНАЛОГ STRTOD() ИЗ QT
double QString::toDouble ( bool * ok = 0 ) const
Returns the string converted to a double value.
Returns 0.0 if the conversion fails.
If a conversion error occurs, *ok is set to false; otherwise *ok is set to true.
Various string formats for floating point numbers can be converted to double values.
This function tries to interpret the string according to the current locale. The current locale is determined from the system at application startup and can be changed by calling QLocale::setDefault(). If the string cannot be interpreted according to the current locale, this function falls back on the "C" locale.
Due to the ambiguity between the decimal point and thousands group separator in various locales, this function does not handle thousands group separators. If you need to convert such numbers, see QLocale::toDouble().
See also number(), QLocale::setDefault(), QLocale::toDouble(), and trimmed().

ПРИМЕР VIII – DOM
http://www.w3.org/DOM/DOMTR
Основные документы
Core http://www.w3.org/TR/2004/REC-DOM-Level-3-Core-20040407
HTML http://www.w3.org/TR/2003/REC-DOM-Level-2-HTML-20030109
Style (StyleSheets + CSS)http://www.w3.org/TR/2000/REC-DOM-Level-2-Style-20001113
Traversal and Range http://www.w3.org/TR/2000/REC-DOM-Level-2-Traversal-Range-20001113
Load-Save http://www.w3.org/TR/2004/REC-DOM-Level-3-LS-20040407
Validation http://www.w3.org/TR/2004/REC-DOM-Level-3-Val-20040127
Element Traversal http://www.w3.org/TR/2008/REC-ElementTraversal-20081222
Xpath http://www.w3.org/TR/2004/NOTE-DOM-Level-3-XPath-20040226
Views and Formatting http://www.w3.org/TR/2004/NOTE-DOM-Level-3-Views-20040226
Events http://www.w3.org/TR/2009/WD-DOM-Level-3-Events-20090908
http://www.w3.org/TR/2009/WD-eventsource-20091222/
Дополнительные части
DOM Events http://www.w3.org/TR/#tr_DOM_events
MathML http://www.w3.org/TR/#tr_MathML
SMIL http://www.w3.org/TR/#tr_SMIL
SVG http://www.w3.org/TR/#tr_SVG
http://www.w3.org/TR/#tr_SVG_Tiny

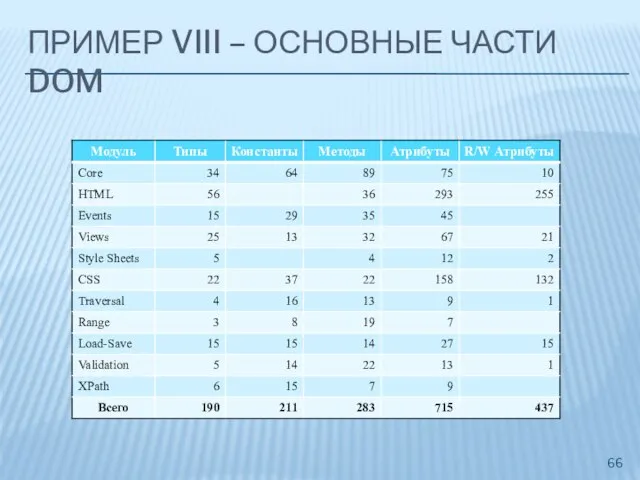
ПРИМЕР VIII – ОСНОВНЫЕ ЧАСТИ DOM

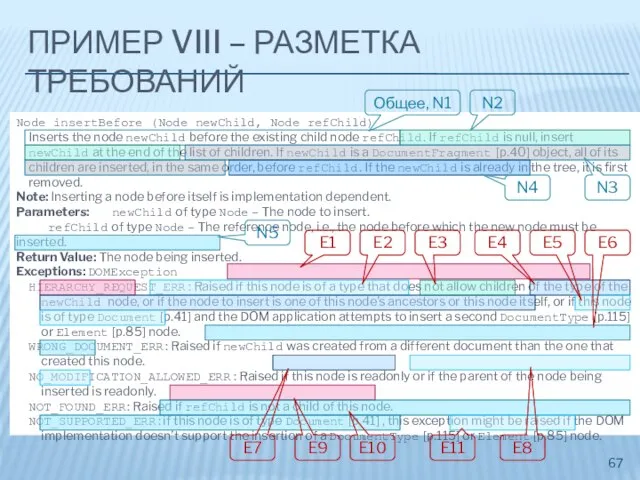
ПРИМЕР VIII – РАЗМЕТКА ТРЕБОВАНИЙ
Node insertBefore (Node newChild, Node refChild)
Inserts the node newChild before the existing child node refChild. If refChild is null, insert newChild at the end of the list of children. If newChild is a DocumentFragment [p.40] object, all of its children are inserted, in the same order, before refChild. If the newChild is already in the tree, it is first removed.
Note: Inserting a node before itself is implementation dependent.
Parameters: newChild of type Node – The node to insert.
refChild of type Node – The reference node, i.e., the node before which the new node must be inserted.
Return Value: The node being inserted.
Exceptions: DOMException
HIERARCHY_REQUEST_ERR: Raised if this node is of a type that does not allow children of the type of the newChild node, or if the node to insert is one of this node’s ancestors or this node itself, or if this node is of type Document [p.41] and the DOM application attempts to insert a second DocumentType [p.115] or Element [p.85] node.
WRONG_DOCUMENT_ERR: Raised if newChild was created from a different document than the one that created this node.
NO_MODIFICATION_ALLOWED_ERR: Raised if this node is readonly or if the parent of the node being inserted is readonly.
NOT_FOUND_ERR: Raised if refChild is not a child of this node.
NOT_SUPPORTED_ERR: if this node is of type Document [p.41] , this exception might be raised if the DOM implementation doesn’t support the insertion of a DocumentType [p.115] or Element [p.85] node.
Общее, N1
N2
N3
N4
N5
E1
E2
E3
E4
E5
E6
E7
E8
E9
E10
E11

ПРИМЕР VIII – НЕОДНОЗНАЧНОСТИ
Что имеется в виду под «the node being inserted»?
DocumentFragment или его элемент?
Что будет при вставке null?
При вставке DocumentFragment
Что будет результатом?
Как изменится список «детей» при некорректном «ребенке» в конце?
Можно ли добавить пустой DocumentFragment, если добавлять «детей» нельзя?
Как определить, поддерживается ли вставка DocumentType и Element?
Почему нет ограничений на порядок «детей» в Document?

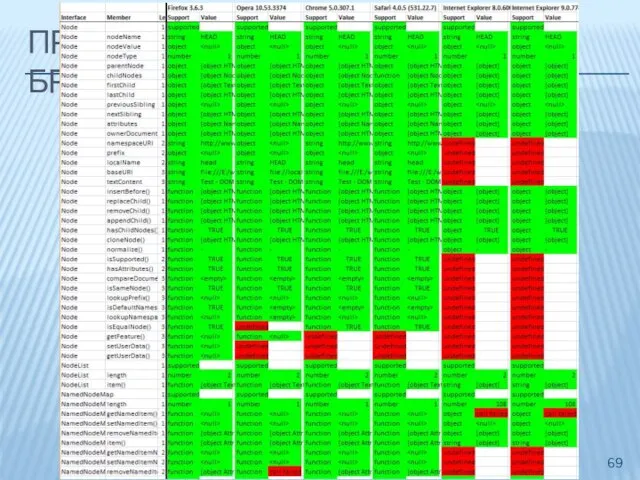
ПРИМЕР VIII – ПОДДЕРЖКА В БРАУЗЕРАХ

ЗАКЛЮЧЕНИЕ I
«Классические» формальные методы слишком трудоемки для подавляющего большинства сложных задач
Формализация требований одна уже дает многие их бонусы
Позволяет проводить строгий анализ задачи
Оставляет затраты приемлемыми
При дополнении автоматизированными техниками верификации работает во многих практически значимых ситуациях

ЗАКЛЮЧЕНИЕ II
Формализация – не панацея
Не гарантирует адекватности модели, для этого нужны дополнительные усилия
В сложных случаях все-таки очень сложна
Нужны компонентные методы построения и анализа формальных моделей
Есть надежда, что они позволят эффективно работать со сверхсложными моделями