Содержание
- 2. Ch1_ Ch1_ Definition An equation such as x+3y=9 is called a linear equation (in two variables
- 3. Ch1_ Ch1_ Definition A linear equation in n variables x1, x2, x3, …, xn has the
- 4. Ch1_ Ch1_ Solutions for system of linear equations Figure 1.1 Unique solution x + 3y =
- 5. Ch1_ Ch1_ A linear equation in three variables corresponds to a plane in three-dimensional space. ※
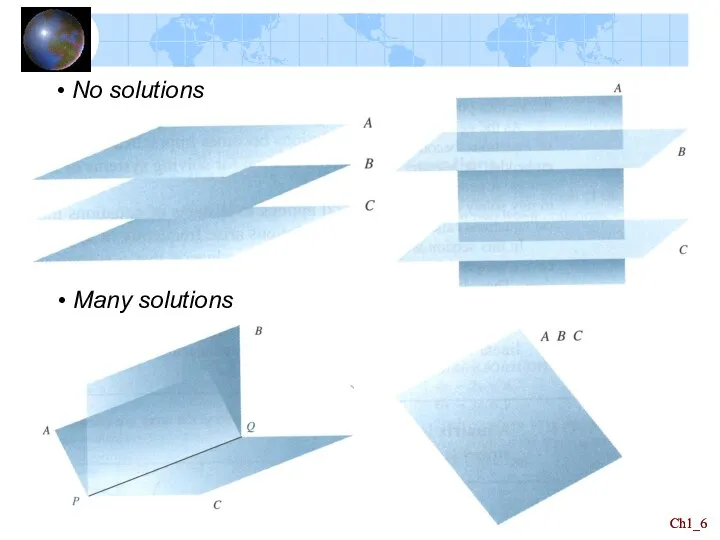
- 6. Ch1_ Ch1_
- 7. Ch1_ Ch1_ A solution to a system of a three linear equations will be points that
- 8. Ch1_ Ch1_ Definition A matrix is a rectangular array of numbers. The numbers in the array
- 9. Ch1_ Ch1_ Submatrix Row and Column
- 10. Ch1_ Ch1_
- 11. Ch1_ Ch1_ matrix of coefficients and augmented matrix Relations between system of linear equations and matrices
- 12. Ch1_ Ch1_ Elementary Transformation Interchange two equations. Multiply both sides of an equation by a nonzero
- 13. Ch1_ Ch1_ Example 1 Solving the following system of linear equation.
- 14. Ch1_ Ch1_
- 15. Ch1_ Ch1_ Example 2 Solving the following system of linear equation. Solution
- 16. Ch1_ Ch1_ Example 3 Solve the system Solution
- 17. Ch1_ Ch1_ Summary Use row operations to [A: B] : Def. [In : X] is called
- 18. Ch1_ Ch1_ Example 4 Many Systems Solving the following three systems of linear equation, all of
- 19. Ch1_ Ch1_ Homework Exercises will be given by the teachers of the practical classes.
- 20. Ch1_ Ch1_ 1.2 Gauss-Jordan Elimination Definition A matrix is in reduced echelon form if Any rows
- 21. Ch1_ Ch1_ Examples for reduced echelon form (✓) (✓) (?) (?) elementary row operations,reduced echelon form
- 22. Ch1_ Ch1_ Gauss-Jordan Elimination System of linear equations ⇒ augmented matrix ⇒ reduced echelon form ⇒
- 23. Ch1_ Ch1_ Example 1 Use the method of Gauss-Jordan elimination to find reduced echelon form of
- 24. Ch1_ Ch1_ Example 2 Solve, if possible, the system of equations Solution The general solution to
- 25. Ch1_ Ch1_ Example 3 Solve the system of equations Solution ⇒ many sol.
- 26. Ch1_ Ch1_ Example 4 Solve the system of equations Solution
- 27. Ch1_ Ch1_ Example 5 This example illustrates a system that has no solution. Let us try
- 28. Ch1_ Ch1_ Homogeneous System of linear Equations Definition A system of linear equations is said to
- 29. Ch1_ Ch1_ Homogeneous System of linear Equations Note. Non trivial solution
- 30. Ch1_ Ch1_ Homework Exercise will be given by the teachers of the practical classes.
- 31. Ch1_ 1.3 Gaussian Elimination Definition A matrix is in echelon form if Any rows consisting entirely
- 32. Ch1_ Example 6 Solving the following system of linear equations using the method of Gaussian elimination.
- 33. Ch1_ The corresponding system of equation is
- 34. Ch1_ Example 7 Solving the following system of linear equations using the method of Gaussian elimination,
- 36. Скачать презентацию














![Ch1_ Ch1_ Summary Use row operations to [A: B] : Def. [In](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/999769/slide-16.jpg)

















 Особенности лечения артериальной гипертензии у беременных
Особенности лечения артериальной гипертензии у беременных Психологическая готовность обучающихся к сдаче экзаменов
Психологическая готовность обучающихся к сдаче экзаменов Аквагрим
Аквагрим  СмешиваниеСглаживаниеТуманПараметры точки
СмешиваниеСглаживаниеТуманПараметры точки Теория государства и права – 3. Нормы права – диспозитивные и императивные
Теория государства и права – 3. Нормы права – диспозитивные и императивные Бизнес-план. Кафе Chocolate
Бизнес-план. Кафе Chocolate Профессиональные ансамбли народного танца
Профессиональные ансамбли народного танца Гра Спіймай колір - альфа версія
Гра Спіймай колір - альфа версія Маркетинговая деятельность в учреждениях среднего профессионального образования
Маркетинговая деятельность в учреждениях среднего профессионального образования Анализ применения систем биллинга операторами сотовой связи в России и странах СНГ
Анализ применения систем биллинга операторами сотовой связи в России и странах СНГ День славянской письменности
День славянской письменности Государственная итоговая аттестация по образовательным программам среднего общего образования на территории Тульской области
Государственная итоговая аттестация по образовательным программам среднего общего образования на территории Тульской области Феварин в терапии алкогольной зависимости
Феварин в терапии алкогольной зависимости Программа повышения компетенций менеджмента компании
Программа повышения компетенций менеджмента компании Основы психологии. 8 класс
Основы психологии. 8 класс Www.indoormedia.org.ua. Оператор Indoor-radio и Indoor-TV в супермаркетах, ТРЦ Оператор Indoor-TV в сети аптек. Оператор Indoor-TV на железнодорожных.
Www.indoormedia.org.ua. Оператор Indoor-radio и Indoor-TV в супермаркетах, ТРЦ Оператор Indoor-TV в сети аптек. Оператор Indoor-TV на железнодорожных. Преобразование выражений, содержащих квадратные корни Подготовила учитель математики Ванюкова Любовь Геннадьевна
Преобразование выражений, содержащих квадратные корни Подготовила учитель математики Ванюкова Любовь Геннадьевна Бизнес - школа дизайнеров
Бизнес - школа дизайнеров Место и время счастья
Место и время счастья МоскваГостиный Двор12-15 сентября2012
МоскваГостиный Двор12-15 сентября2012 Укрепление системы органов внутренних дел во второй половине 1960-х - 1980-е гг
Укрепление системы органов внутренних дел во второй половине 1960-х - 1980-е гг История ВФСК Готов к труду и обороне
История ВФСК Готов к труду и обороне Порядок подачи апелляций
Порядок подачи апелляций Проект “Контроль”
Проект “Контроль” Изменение агентского договора с пунктами выдачи Faberlic
Изменение агентского договора с пунктами выдачи Faberlic ФГОС-2021
ФГОС-2021 Стратегия и тактика спора. Логические и психологические приемы дискуссии и полемики
Стратегия и тактика спора. Логические и психологические приемы дискуссии и полемики Предмет, метод, система и источники трудового права
Предмет, метод, система и источники трудового права