Ch2-Matrices

Ch2_
2.1 Addition, Scalar Multiplication, and Multiplication of Matrices
Definition
Two matrices are equal if they are of the same size and if their corresponding elements are equal.
aij: the element of matrix A in row i and column j.
For a square n×n matrix A, the main diagonal is:
Thus A = B if aij = bij ∀ i, j.
(∀ for every, for all)

Ch2_
Addition of Matrices
Definition
Let A and B be matrices of the same size.
Their sum A + B is the matrix obtained by adding together the corresponding elements of A and B.
The matrix A + B will be of the same size as A and B.
If A and B are not of the same size, they cannot be added, and we say that the sum does not exist.

Ch2_
Example 1
Solution
(2) Because A is 2 × 3 matrix and C is a 2 × 2 matrix, they are not of the same size, A + C does not exist.

Ch2_
Scalar Multiplication of matrices
Definition
Let A be a matrix and c be a scalar. The scalar multiple of A by c, denoted cA, is the matrix obtained by multiplying every element of A by c. The matrix cA will be the same size as A.

Ch2_
Negation and Subtraction
Definition
We now define subtraction of matrices in such a way that makes it compatible with addition, scalar multiplication, and negative. Let
A – B = A + (–1)B

Ch2_
Multiplication of Matrices
Definition
Let the number of columns in a matrix A be the same as the number of rows in a matrix B. The product AB then exists.
If the number of columns in A does not equal the number of row B,
we say that the product does not exist.
Let A: m×n matrix, B: n×k matrix,
The product matrix C=AB has elements
C is a m×k matrix.

Ch2_
Example 4
BA and AC do not exist.
Solution.
Note. In general, AB≠BA.

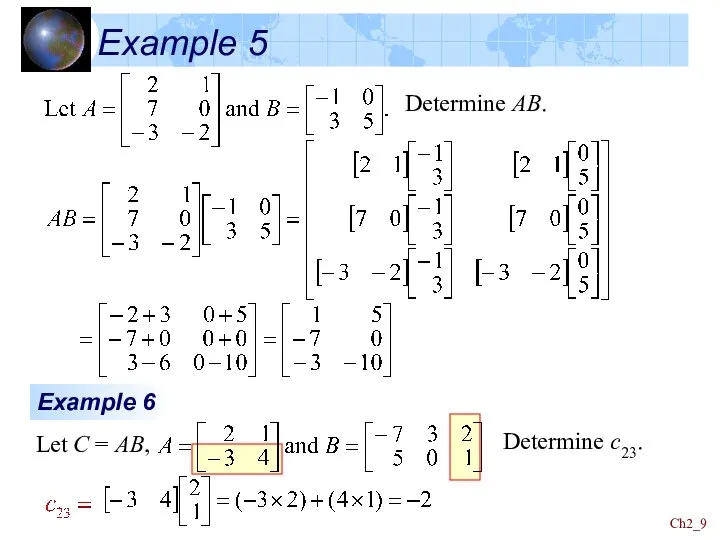
Ch2_
Example 5
Determine AB.

Ch2_
Size of a Product Matrix
If A is an m × r matrix and B is an r × n matrix, then AB will be an m × n matrix.
B
r × n
= AB
m × n

Ch2_
Definition
A zero matrix is a matrix in which all the elements are zeros.
A diagonal matrix is a square matrix in which all the elements not on the main diagonal are zeros.
An identity matrix is a diagonal matrix in which every diagonal element is 1.
Special Matrices

Ch2_
Theorem 2.1
Let A be m × n matrix and Omn be the zero m × n matrix. Let B be an n × n square matrix. On and In be the zero and identity n × n matrices. Then
A + Omn = Omn + A = A
BOn = OnB = On
BIn = InB = B

Ch2_
Homework
Exercises will be given by the teachers of the practical classes.
Solution

Ch2_
2.2 Algebraic Properties of Matrix Operations
Theorem 2.2 -1
Let A, B, and C be matrices and a, b, and c be scalars. Assume that the size of the matrices are such that the operations can be performed.
Properties of Matrix Addition and scalar Multiplication
1. A + B = B + A Commutative property of addition
2. A + (B + C) = (A + B) + C Associative property of addition
3. A + O = O + A = A (where O is the appropriate zero matrix)
4. c(A + B) = cA + cB Distributive property of addition
5. (a + b)C = aC + bC Distributive property of addition
6. (ab)C = a(bC)

Ch2_
Let A, B, and C be matrices and a, b, and c be scalars. Assume that the size of the matrices are such that the operations can be performed.
Properties of Matrix Multiplication
1. A(BC) = (AB)C Associative property of multiplication
2. A(B + C) = AB + AC Distributive property of multiplication
3. (A + B)C = AC + BC Distributive property of multiplication
4. AIn = InA = A (where In is the appropriate identity matrix)
5. c(AB) = (cA)B = A(cB)
Note: AB≠ BA in general. Multiplication of matrices is not commutative.
Theorem 2.2 -2

Ch2_
Proof of Theorem 2.2 (A+B=B+A)
Consider the (i,j)th elements of matrices A+B and B+A:
∴ A+B=B+A

Ch2_
Arithmetic Operations
If A is an m × r matrix and B is r × n matrix, the number of scalar multiplications involved in computing the product AB is mrn.
Consider three matrices A, B and C such that the product
ABC exists.
Compare the number of multiplications involved in the
two ways (AB)C and A(BC) of computing the product ABC

Ch2_
Example 10
Count the number of multiplications.
Which method is better?
2×6+3×2
=12+6=18
3×2+2×2
=6+4=10
∴ A(BC) is better.

Ch2_
In algebra we know that the following cancellation laws apply.
If ab = ac and a ≠ 0 then b = c.
If pq = 0 then p = 0 or q = 0.
However the corresponding results are not true for matrices.
AB = AC does not imply that B = C.
PQ = O does not imply that P = O or Q = O.
Caution
Example 11

Ch2_
Powers of Matrices
Theorem 2.3
If A is an n × n square matrix and r and s are nonnegative integers, then
1. ArAs = Ar+s.
2. (Ar)s = Ars.
3. A0 = In (by definition)
Definition
If A is a square matrix, then

Ch2_
Example 12
Solution

Ch2_
Systems of Linear Equations
A system of m linear equations in n variables as follows
Let
We can write the system of equations in the matrix form
AX = B

Ch2_
Idempotent and Nilpotent Matrices
Definition
A square matrix A is said to be idempotent if A2=A.
A square matrix A is said to nilpotent if there is a positive integer p such that Ap=0. The least integer p such that
Ap=0 is called the degree of nilpotency of the matrix.
Example 14

Ch2_
Homework
Exercises will be given by the teachers of the practical classes.

Ch2_
2.3 Symmetric Matrices
Definition
The transpose of a matrix A, denoted At, is the matrix whose columns are the rows of the given matrix A.

Ch2_
Theorem 2.4: Properties of Transpose
Let A and B be matrices and c be a scalar. Assume that the sizes of the matrices are such that the operations can be performed.
1. (A + B)t = At + Bt Transpose of a sum
2. (cA)t = cAt Transpose of a scalar multiple
3. (AB)t = BtAt Transpose of a product
4. (At)t = A

Ch2_
Symmetric Matrix
Definition
A symmetric matrix is a matrix that is equal to its transpose.
Example 16

Ch2_
Remark: If and only if
Let p and q be statements.
Suppose that p implies q (if p then q), written p ⇒ q,
and that also q ⇒ p, we say that
“p if and only if q” (in short iff )

Ch2_
Example 17
*We have to show (a) AB is symmetric ⇒ AB = BA, and the converse, (b) AB is symmetric ⇐ AB = BA.
(⇒) Let AB be symmetric, then
AB= (AB)t by definition of symmetric matrix
= BtAt by Thm 2.4 (3)
= BA since A and B are symmetric
(⇐) Let AB = BA, then
(AB)t = (BA)t
= AtBt by Thm 2.4 (3)
= AB since A and B are symmetric
Proof
Let A and B be symmetric matrices of the same size. Prove that the product AB is symmetric if and only if AB = BA.

Ch2_
Example 18
Proof
Let A be a symmetric matrix. Prove that A2 is symmetric.

Homework
Exercises will be given by the teachers of the practical classes.

Ch2_
2.4 The Inverse of a Matrix
Definition
Let A be an n × n matrix. If a matrix B can be found such that
AB = BA = In, then A is said to be invertible and B is called the inverse of A. If such a matrix B does not exist, then A has no inverse. (denote B = A−1, and A−k=(A−1)k )
Thus AB = BA = I2, proving that the matrix A has inverse B.

Ch2_
Theorem 2.5
The inverse of an invertible matrix is unique.
Proof
Let B and C be inverses of A.
Thus AB = BA = In, and AC = CA = In.
Multiply both sides of the equation AB = In by C.
C(AB) = CIn
(CA)B = C
InB = C
B = C
Thus an invertible matrix has only one inverse.

Ch2_
Gauss-Jordan Elimination for finding the Inverse of a Matrix
Let A be an n × n matrix.
1. Adjoin the identity n × n matrix In to A to form the matrix [A : In].
2. Compute the reduced echelon form of [A : In].
If the reduced echelon form is of the type [In : B], then B is the inverse of A.
If the reduced echelon form is not of the type [In : B], in that the first n × n submatrix is not In, then A has no inverse.
An n × n matrix A is invertible if and only if its reduced echelon form is In.

Ch2_
Example 20
Solution

Ch2_
Example 21
Determine the inverse of the following matrix, if it exist.
Solution
There is no need to proceed further.
The reduced echelon form cannot have a one in the (3, 3) location.
The reduced echelon form cannot be of the form [In : B].
Thus A–1 does not exist.

Ch2_
Properties of Matrix Inverse
Let A and B be invertible matrices and c a nonzero scalar, Then
Proof
1. By definition, AA−1=A−1A=I.

Ch2_
Solution

Ch2_
Theorem 2.6
Let AX = B be a system of n linear equations in n variables.
If A–1 exists, the solution is unique and is given by X = A–1B.
Proof
(X = A–1B is a solution.)
Substitute X = A–1B into the matrix equation.
AX = A(A–1B) = (AA–1)B = In B = B.
(The solution is unique.)
Let Y be any solution, thus AY = B. Multiplying both sides of this equation by A–1 gives
A–1A Y= A–1B In Y= A–1B
Y = A–1B. Then Y=X .

Ch2_
Example 22
Solution

Ch2_
Elementary Matrices
Definition
An elementary matrix is one that can be obtained from the identity matrix In through a single elementary row operation.
Example 23

Ch2_
Elementary Matrices
。 Elementary row operation
。 Elementary matrix

Ch2_
Notes for elementary matrices
Each elementary matrix is invertible.
Example 24
If A and B are row equivalent matrices and A is invertible, then B is invertible.
Proof
If A ≈ … ≈ B, then
B=En … E2 E1 A for some elementary matrices En, … , E2 and E1.
So B−1 = (En … E2 E1A)−1 =A−1E1−1 E2−1 … En−1.