Содержание
- 2. ЦІЛІ: отримати знання з найбільш вживаних чисельних методів розв’язання математичних задач; отримати навички програмування типових обчислювальних
- 3. ОРГАНІЗАЦІЯ КУРСУ: лекції – викладення теоретичного матеріалу; лабораторні роботи – реалізація чисельних методів на ЕОМ та
- 4. Використання ЕОМ при розв’язанні задач
- 5. Достовірність результатів вимірюється їх похибкою
- 6. Похибка округлень Якщо число подане у системі з основою p у вигляді: 0.α1 α2 α3…αn •
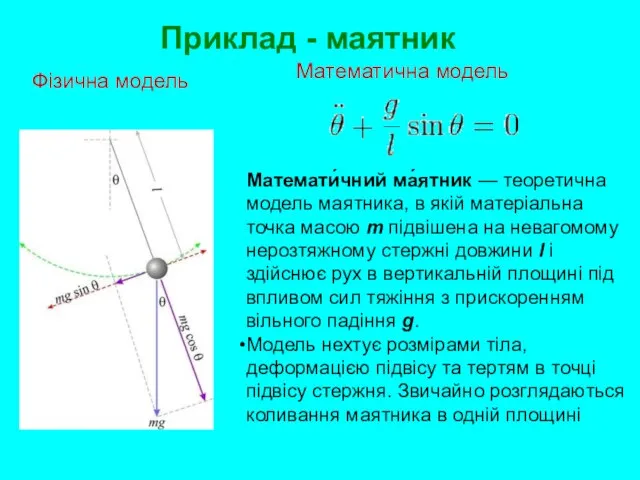
- 7. Приклад - маятник Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена
- 8. Спрощена модель При малих коливаннях і рівняння руху маятника зводиться до рівняння гармонічного осцилятора де частота
- 9. Інший приклад
- 10. Математична модель – система нелінійних диференційних рівнянь
- 11. "MSC Napoli" на мілині після аварії Протока Ла-Манш, січень 2007 L= 275 м, D = 53,4
- 12. Тріщина у корпусі "MSC Napoli" Результат шторму з висотою хвиль до 9 м Теоретичні дослідження: руйнування
- 13. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ НЕЛІНІЙНИХ РІВНЯНЬ
- 14. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ НЕЛІНІЙНИХ РІВНЯНЬ 1) Локалізувати корінь a 2) Уточнити корінь до припустимої похибки δx
- 15. МЕТОДИ УТОЧНЕННЯ КОРЕНЯ
- 17. Скачать презентацию













 Та ырыпқ Жасанды оректік ортада сетін
Та ырыпқ Жасанды оректік ортада сетін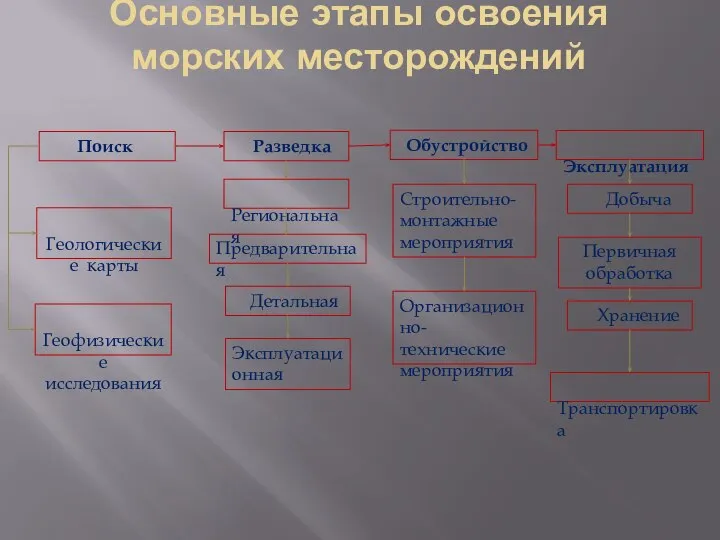 Основные этапы освоения морских месторождений
Основные этапы освоения морских месторождений Открытый урок по технологии Моделирование фартука
Открытый урок по технологии Моделирование фартука Особенности восприятия социальной действительности ммальчиками и девочками
Особенности восприятия социальной действительности ммальчиками и девочками История волейбола
История волейбола Фрейд
Фрейд 20170109_keys_tehnologiya1
20170109_keys_tehnologiya1 Викторина Старый Новый год
Викторина Старый Новый год Спортивный зал
Спортивный зал Анализ сведений представляемых при поступлении на государственную службу
Анализ сведений представляемых при поступлении на государственную службу Каталог географических знаков
Каталог географических знаков Экстрапирамидная система и синдромы ее поражения
Экстрапирамидная система и синдромы ее поражения ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ ИССЛЕ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ ИССЛЕ Чехов Вишнёвый сад
Чехов Вишнёвый сад The “AmurE” Triumph Palace: a Modern interpretation of Classical garden-park Architecture themes / Ppt-presentation by Dr. Konstantin I.Samoilov. – Almaty, 2016. – 46 p.
The “AmurE” Triumph Palace: a Modern interpretation of Classical garden-park Architecture themes / Ppt-presentation by Dr. Konstantin I.Samoilov. – Almaty, 2016. – 46 p. Бег с барьерами
Бег с барьерами Доступные исследования
Доступные исследования Функции управления и связующие процессы
Функции управления и связующие процессы Презентация на тему Типы климатов России
Презентация на тему Типы климатов России Издержки производства и себестоимость продукции (услуг). Лекция 6
Издержки производства и себестоимость продукции (услуг). Лекция 6 Старый Оскол - Твой город! Твое решение! Твое будущее!
Старый Оскол - Твой город! Твое решение! Твое будущее! Требования к кандидатам, поступающим на военную службу по контракту
Требования к кандидатам, поступающим на военную службу по контракту Логистическая миссия и корпоративная стратегия
Логистическая миссия и корпоративная стратегия НПП «Цифровые решения»
НПП «Цифровые решения» Презентация на тему Состав основных фондов
Презентация на тему Состав основных фондов  Kazakhstan in 70 -1991 years
Kazakhstan in 70 -1991 years Презентация на тему Архитектура Древнего Египта
Презентация на тему Архитектура Древнего Египта Значение языка в жизни человека
Значение языка в жизни человека