Числа Фибоначчи (7 класс)

Историческая справка
Определение чисел Фибоначчи
Свойства чисел Фибоначчи
Спираль Фибоначчи
Пропорции Фибоначчи в природе
Пропорции Фибоначчи в архитектуре
Пропорции Фибоначчи в космосе
Выводы
Содержание

Леонардо Пизанский (Фибоначчи)
( около 1170 – около 1250 гг.)
г.Пиза, в семье дипломата
Первый крупный математик средневековой Европы

В молодости часто бывал в Алжире. Изучал там математику у арабских учителей
Позже посетил Египет, Сирию, Византию, Сицилию. Везде изучал труды математиков
По арабским переводам ознакомился с достижениями античных и индийских математиков
На основе усвоенных им знаний Фибоначчи написал ряд выдающихся математических трактатов

«Книга абака» (1202 г.) - содержит почти все арифметические и алгебраические сведения того времени
«Практика геометрии» (1220 г.) - содержит теоремы, относящиеся к измерительным методам
Трактат «Цветок» (1225 г.) - исследование кубического уравнения
«Книга квадратов» (1225) - ряд задач на решение неопределенных квадратных уравнений
Научная деятельность Фибоначчи

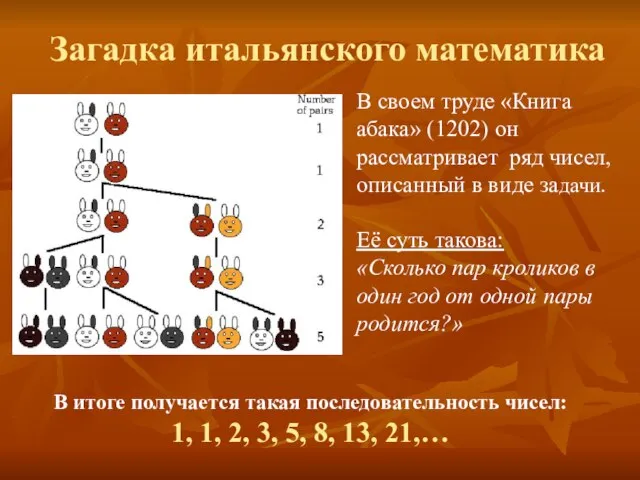
В своем труде «Книга абака» (1202) он рассматривает ряд чисел, описанный в виде задачи.
Её суть такова:
«Сколько пар кроликов в один год от одной пары родится?»
В итоге получается такая последовательность чисел:
1, 1, 2, 3, 5, 8, 13, 21,…
Загадка итальянского математика

Числа Фибоначчи – элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
в которой каждое последующее число, начиная с третьего, равно сумме двух предыдущих чисел, первые два числа считаются заданными - это числа 1 и 1. Т.е. при всяком n > 2
un=un-1+un-2 , и u1=1 и u2=1
Эта последовательность была известна ещё в древней Индии, где она применялась в метрических науках
Числа Фибоначчи

Отношение какого-либо элемента последовательности к предшествующему ему колеблется около числа 1,618…, через раз то превосходя, то не достигая его:
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377, …
Свойства последовательности Фибоначчи

Отношение какого-либо элемента последовательности к последующему приближается к числу 0,618…, что обратно пропорционально числу 1,618…
Если делить элементы последовательности через один, то получим числа 2,618… и 0,382…, которые так же являются взаимно обратными числами
Каждое третье число чётное, каждое четвёртое делится на 3, каждое пятое - на 5, каждое пятнадцатое – на10
Невозможно построить треугольник, сторонами которого являются числа ряда Фибоначчи (никакое число ряда не может повторяться дважды)
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377,…

Иррациональное число "фи" (Ф=1,618…) - «Золотое сечение», «Золотое среднее», «Отношение вертящихся квадратов»
0,618… - «Золотая пропорция»
Особые названия соотношений

Спираль Фибоначчи.
Прямоугольник с шириной и длиной равными двум соседним числам Фибоначчи называют «золотым» прямоугольником
Если разбивать его на более мелкие «золотые» прямоугольники и разделить каждый из них дугой, то система приобретет форму спирали, у которой есть начало, но нет конца

Еще немецкий поэт Гёте подчеркивал тенденцию природы к спиральности. Спираль видна в ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган.
Чешуйки на поверхности сосновой шишки расположены строго закономерно - по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21.
Расстояние между листьями (или ветками на стволе растения) относятся примерно как числа Фибоначчи.
Пропорции Фибоначчи в природе

Данную спираль можно
увидеть в раковине моллюска
Расположение семечек и цветов броколли – идеальная последовательность спиралей
Данную спираль можно
увидеть в раковине моллюска
Расположение семечек и цветов броколли – идеальная последовательность спиралей
Данную спираль можно
увидеть в раковине моллюска
Расположение семечек и цветов броколли – идеальная последовательность спиралей

Пирамиды в Гизе
Пирамиды Майя в Мексике
Во всех внешних и внутренних пропорциях пирамид число 1,618… играет центральную роль
Пропорции Фибоначчи в архитектуре

Рукава многих спиралевидных галактик расположены в соответствии с этой последовательностью
Пропорции Фибоначчи в космосе

В результате работы я познакомился с числами Фибоначчи
Числа Фибоначчи – это красиво, серьёзно, актуально
Числа Фибоначчи имеют различное проявление в природе, архитектуре, космосе
При выполнении работы я убедился, что природа сама творит красоту по законам математики
Выводы