Численное моделирование СВЧ нагрева многослойных диэлектриков

Цель и актуальность.
Цель: Построить численную модель СВЧ нагрева многослойных диэлектриков
Актульность: избирательный, равномерный, сверхчистый, саморегулирующейся нагрев

Физическая постановка задачи
Диэлектрик: трехслойная структура, где две пластины соединяются между собой клеющем веществом.
и
Значит слой клея будет нагреваться быстрее, чем другие слои.
У клея ускорится процесс полимеризации

Падение и отражение СВЧ лучей на слои диэлектриков
Рис. 1. схематическая модель диэлектрика

Определение коэффициентов прохождения и отражения
Комплексная амплитуда напряженности магнитного поля
- волновое сопротивление воздуха
Комплексные амплитуды полей в i-ом слое:

Система 1.
Система уравнений для определения коэфиценов прохождения и отражения

Температурное поле в плоскослоистой структуре
Начальные и граничные условия выбираются в виде :
Система 2.

(5).
( 4).
(3).
(2).
(1).
m=1,2,3.
Для построения консервативной разностной схемы в одномерной области
вводится в каждом слое равномерная по координате z сетка

(8).
(7).
(6).
Уравнение теплового баланса для элементарной ячейки
Обозначим
значения температуры в узлах сетки
Где
-тепловые потоки на границах элементарной
ячейки

(11).
(10).
(9).
разностное уравнение для внутренних точек
разностное уравнение для
левой границы:
Для элементарной ячейки, содержащей узел, принадлежащий границе слоев,
разностное уравнение имеет вид
m=2,3

(13).
(12).
Записав уравнение теплового баланса для элементарной ячейки
прилегающей к правой левой границе области, получим разностное уравнение для правой границы:
Начальные условия записываются в виде

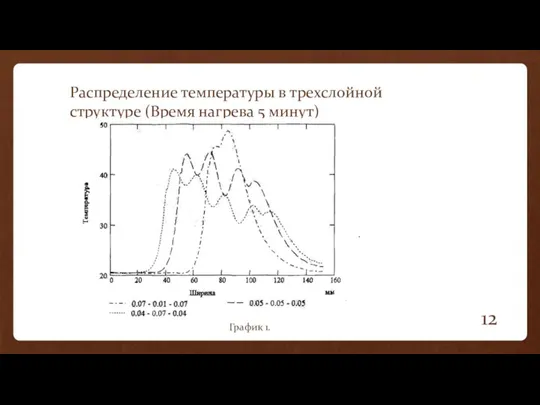
Распределение температуры в трехслойной структуре (Время нагрева 5 минут)
График 1.

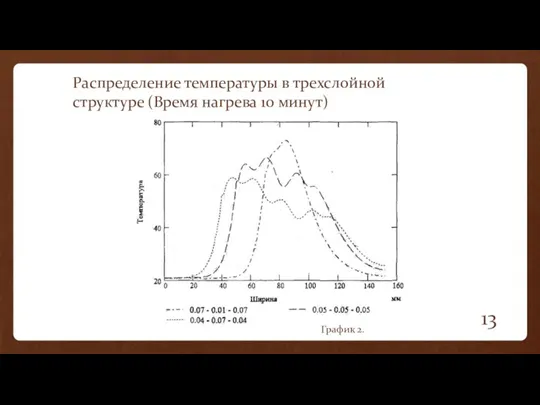
Распределение температуры в трехслойной структуре (Время нагрева 10 минут)
График 2.