Цифровые данные 5-7 класс

Хранение информации
в компьютере
Машинную память удобно представить в виде листа в клетку.
В каждой «клетке» хранится только одно из двух значений: нуль или единица.
Каждая «клетка» памяти называется битом.
Цифры 0 и 1, хранящиеся в «клетках» памяти компьютера, называются значениями битов.

Числовая информация
Текстовая информация
Графическая информация
Двоичное кодирование

Десятичная позиционная система счисления
Десятичная – потому что десять единиц одного разряда составляют одну единицу старшего разряда; для записи чисел используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционная – потому, что одна и та же цифра получает разные количественные значения в зависимости от позиции, которую она занимает в записи числа.

Рассмотрим числовой ряд:
1, 10, 100, 1 000, 10 000, 100 000, …
Любое целое число можно представить в виде суммы разрядных слагаемых – единиц, десятков, сотен, тысяч и т.д., записанных в этом ряду:
1652 = 1×1 000 + 6×100 + 5×10 + 2×1
А теперь рассмотрим другой ряд:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, …
Немного математики

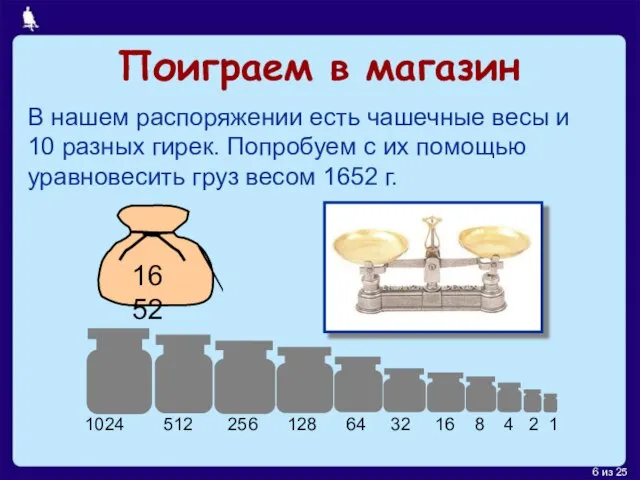
Поиграем в магазин
В нашем распоряжении есть чашечные весы и
10 разных гирек. Попробуем с их помощью уравновесить груз весом 1652 г.
1024 512 256 128 64 32 16 8 4 2 1

Метод разностей
На одну чашу весов ставим груз, а на другую – гирьку с весом, ближайшим к весу груза, но не превышающим его. Найдем разность:
1652 – 1024 = 628.
1024 512 256 128 64 32 16 8 4 2 1
Найдем гирьку с весом, ближайшим к полученной разности, но не превышающим ее: 628 – 512 = 116.

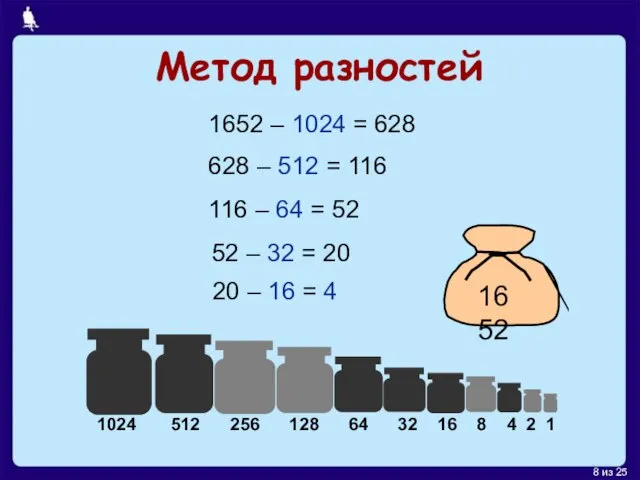
Метод разностей
1652 – 1024 = 628
628 – 512 = 116
1024 512 256 128 64 32 16 8 4 2 1
116 – 64 = 52
52 – 32 = 20
20 – 16 = 4

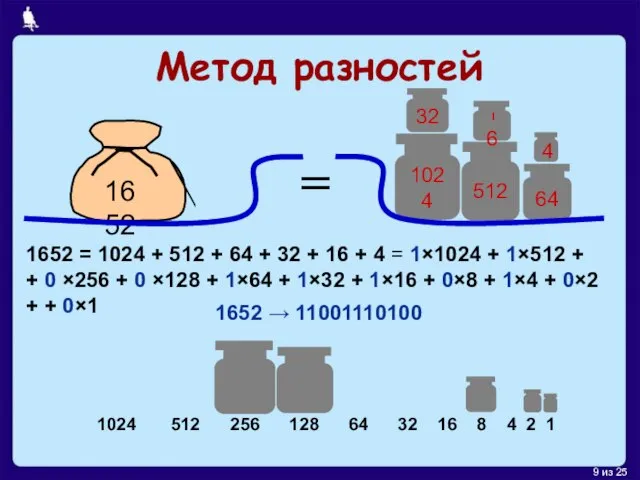
Метод разностей
1652 = 1024 + 512 + 64 + 32 + 16 + 4 = 1×1024 + 1×512 +
+ 0 ×256 + 0 ×128 + 1×64 + 1×32 + 1×16 + 0×8 + 1×4 + 0×2 + + 0×1
1652 → 11001110100
1024 512 256 128 64 32 16 8 4 2 1

Двоичная система счисления
1652 = 1024 + 512 + 64 + 32 + 16 + 4 = 1×1024 + 1×512 +
+ 0 ×256 + 0 ×128 + 1×64 + 1×32 + 1×16 + 0×8 + 1×4 + 0×2 + + 0×1
165410 =110011101002
Мы представили число в двоичной позиционной системе счисления:
двоичной – потому что две единицы одного разряда составляют одну единицу старшего разряда;
для записи чисел используются две цифры: 0 и 1;
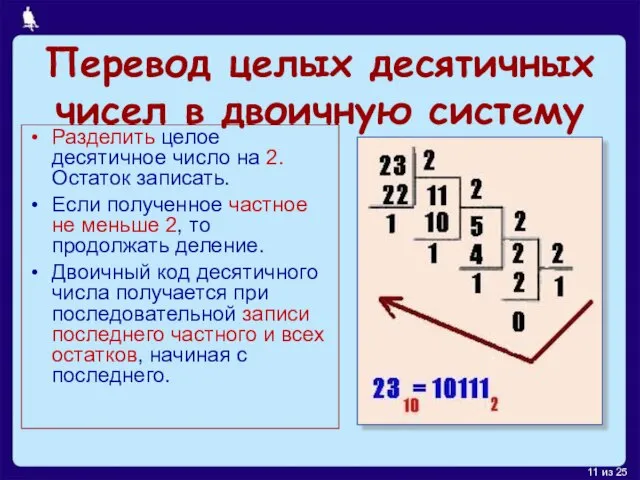
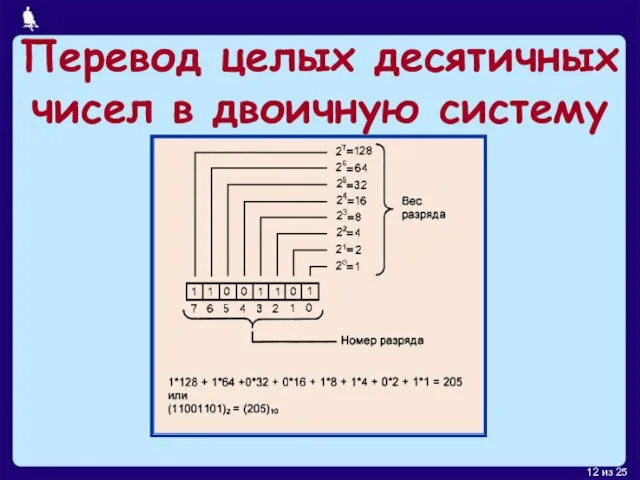
позиционной – потому, что одна и та же цифра получает разные количественные значения в зависимости от позиции, которую она занимает в записи числа.

Перевод целых десятичных чисел в двоичную систему
Разделить целое десятичное число на 2. Остаток записать.
Если полученное частное не меньше 2, то продолжать деление.
Двоичный код десятичного числа получается при последовательной записи последнего частного и всех остатков, начиная с последнего.

Перевод целых десятичных чисел в двоичную систему

Историческая справка
Лейбниц Готфрид Вильгельм (1646 - 1716),
немецкий ученый, заложивший основы
двоичной системы счисления

Двоичное кодирование текстовой информации
Мы знаем, как перевести целое десятичное число в двоичный код.
А если каждому символу текста присвоить номер и по известным правилам перевести это номер в двоичный код?
Т → 210 → 11010010
Именно эта идея положена в основу двоичного кодирования текстовой информации!

Сколько нужно символов?
В текстах мы используем:
прописные и строчные русские буквы Аа Бб Вв …
прописные и строчные латинские буквы Аа Bb Cc …
знаки препинания ! , ? . …
цифры 1 2 3 …
знаки арифметических операций + - × …
другие символы ( [ \ …
Достаточно 256 различных символов.

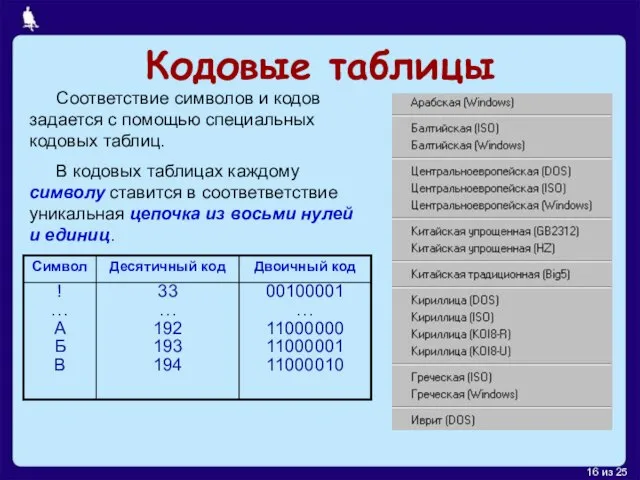
Кодовые таблицы
Соответствие символов и кодов
задается с помощью специальных
кодовых таблиц.
В кодовых таблицах каждому символу ставится в соответветствие уникальная цепочка из восьми нулей и единиц.

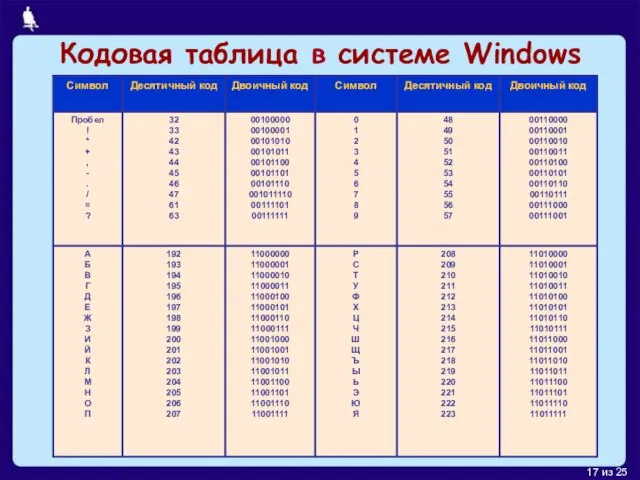
Кодовая таблица в системе Windows

Двоичное кодирование графической информации
Графическое изображение можно разбить на:
крошечные фрагменты;
простейшие геометрические объекты.
На этом основано два варианта двоичного кодирования графической информации:
растровый;
векторный.

Черно-белое изображение
0000000000011100
1000000100000110
1100001100000011
1111111100000011
1101101100000011
1111111100000011
1111111111111110
0111111011111110
0001100011000110
0000000011000110
0000000111001110
0000000111001110
0 – белая клетка
1 – черная клетка

Цветное изображение

Пиксель
Каждый пиксель имеет цвет. Все цвета можно пронумеровать, а каждый номер перевести в двоичный код.
Цветное изображение

Палитра
Необычайно богатая цветовая палитра современных компьютеров (более 16 миллионов оттенков)
получается смешением трех основных цветов:
красного, зеленого и синего.

Векторное кодирование
В графическом объекте можно выделить отдельные фрагменты – прямоугольники, треугольники, окружности, отрезки и т.д. Кодировать можно не сам рисунок, а последовательность команд для его создания.

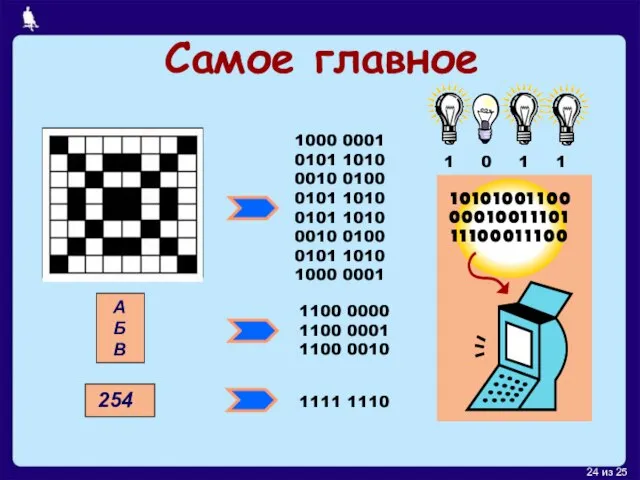
Самое главное
1000 0001
0101 1010
0010 0100
0101 1010
0101 1010
0010 0100
0101 1010
1000 0001
1100 0000
1100 0001
1100 0010
1111 1110
1 0 1 1