цилиндрическим лучом и его
основанием, называется открытым цилиндром. Основание и
образующие цилиндрического луча называют соответственно
основанием и образующими открытого цилиндра.
Конечное тело, ограниченное замкнутой конечной цилиндрической
поверхностью и двумя выделившими её сечениями, называется
конечным цилиндром, или собственно цилиндром. Сечения
называются основаниями цилиндра. По определению конечной
цилиндрической поверхности, основания цилиндра равны.
Очевидно, образующие боковой поверхности цилиндра — равные
по длине (называемой высотой цилиндра) отрезки, лежащие на
параллельных прямых, а концами лежащие на основаниях
цилиндра.
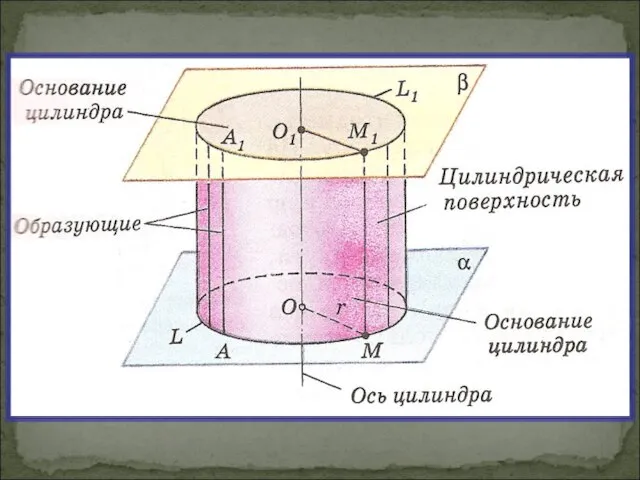
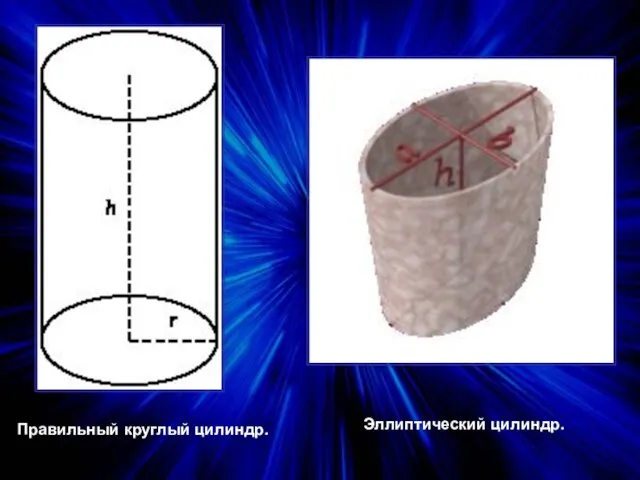
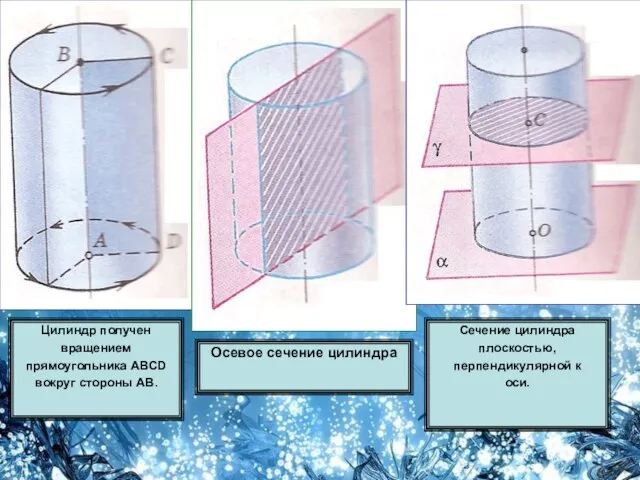
Понятия цилиндра.







 Презентация на тему Размножение и индивидуальное развитие организмов
Презентация на тему Размножение и индивидуальное развитие организмов Руководство по заполнению данных по кадровой потребности
Руководство по заполнению данных по кадровой потребности Biologie. Гастробистро. Звезды Michelin. История успеха Екатерины Алехиной
Biologie. Гастробистро. Звезды Michelin. История успеха Екатерины Алехиной Генетика
Генетика Объединение Альтернативных Операторов связи
Объединение Альтернативных Операторов связи Оранэль. Лесная колода
Оранэль. Лесная колода ПРОЕКТИРОВАНИЕ ГЕНЕРАЛЬНОГО ПЛАНА
ПРОЕКТИРОВАНИЕ ГЕНЕРАЛЬНОГО ПЛАНА Кометы - хвостатые странницы космоса
Кометы - хвостатые странницы космоса Колледж Музыкально - театрального искусства №61
Колледж Музыкально - театрального искусства №61 Наша миссия Разработка проектов, которые станут реальным инструментом поддержки и развития бизнеса наших клиентов.
Наша миссия Разработка проектов, которые станут реальным инструментом поддержки и развития бизнеса наших клиентов. Птичья азбука
Птичья азбука Районный фестиваль-выставка профессионального мастерства педагогов Чудеса мастерства
Районный фестиваль-выставка профессионального мастерства педагогов Чудеса мастерства Animals Wild & domestic
Animals Wild & domestic Только в боге мы находим силу побеждать (фотографии)
Только в боге мы находим силу побеждать (фотографии) Новые цели и ценности в образовании
Новые цели и ценности в образовании «Петра творенье…»
«Петра творенье…» Приливная электростанция (ПЭС)
Приливная электростанция (ПЭС) Информационно-коммуникационные технологии как фактор повышения качества преподавания курса «ОРКСЭ» (1)
Информационно-коммуникационные технологии как фактор повышения качества преподавания курса «ОРКСЭ» (1) Презентация на тему SUPERSTITIONS
Презентация на тему SUPERSTITIONS  Новые виды технологического оборудования, инвентаря, инструментов, посуды кухонной и столовой, новые виды сырья, продуктов
Новые виды технологического оборудования, инвентаря, инструментов, посуды кухонной и столовой, новые виды сырья, продуктов Патологии и феномены в управленческих решениях. (Тема 8)
Патологии и феномены в управленческих решениях. (Тема 8) Уровень Безработицы и пути его снижения в субьекте РФ
Уровень Безработицы и пути его снижения в субьекте РФ Презентация на тему Натуральные числа и шкалы (5 класс)
Презентация на тему Натуральные числа и шкалы (5 класс) ИнформатикаЕГЭУровень - А3
ИнформатикаЕГЭУровень - А3 Съедобные и ядовитые грибы
Съедобные и ядовитые грибы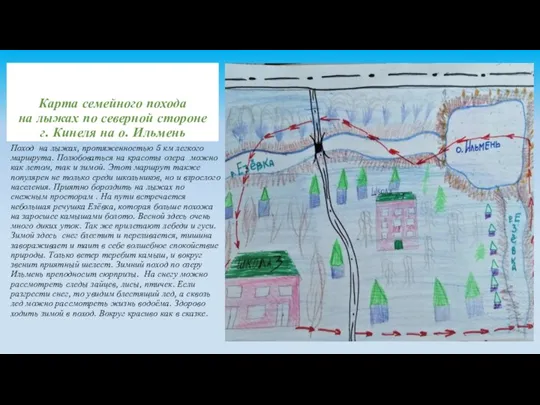 Карта семейного похода
Карта семейного похода Трансформаторы. Назначение и общие сведения о трансформаторах
Трансформаторы. Назначение и общие сведения о трансформаторах Влияние завтрака на здоровье младших школьников
Влияние завтрака на здоровье младших школьников