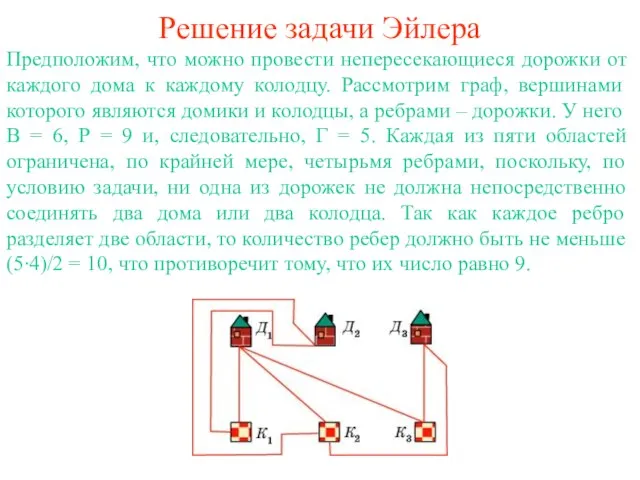
+ Г = 2, где В - число вершин, Р - общее число ребер, Г - число областей (граней), на которые граф разбивает плоскость.
Доказательство. Стянем какое-нибудь ребро графа, соединяющее две вершины, в точку. При этом число ребер и число вершин уменьшаться на единицу и, следовательно, В – Р + Г не измениться. Продолжая стягивать ребра, мы придем к графу, у которого имеется одна вершина, а ребрами являются петли. Уберем какое-нибудь ребро. При этом число ребер и число областей уменьшаться на единицу и, следовательно, В – Р + Г не изменится. Продолжая убирать ребра, мы придем к графу, у которого имеется одна вершина и одно ребро. У этого графа В = 1, Р = 1, Г = 2 и, следовательно, В – Р + Г = 2. Значит, для исходного графа также выполняется равенство В – Р + Г = 2.

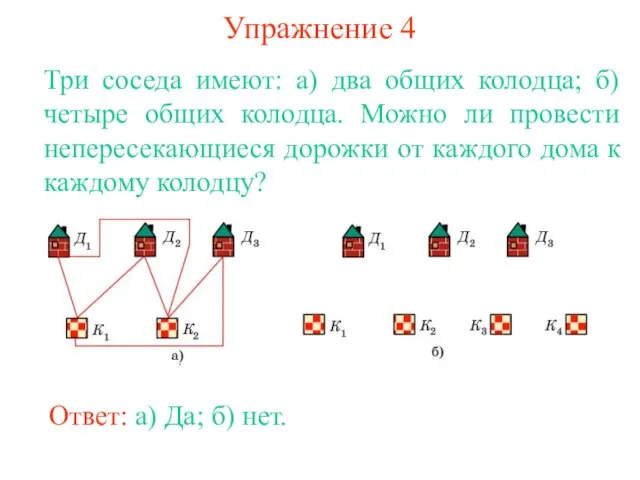
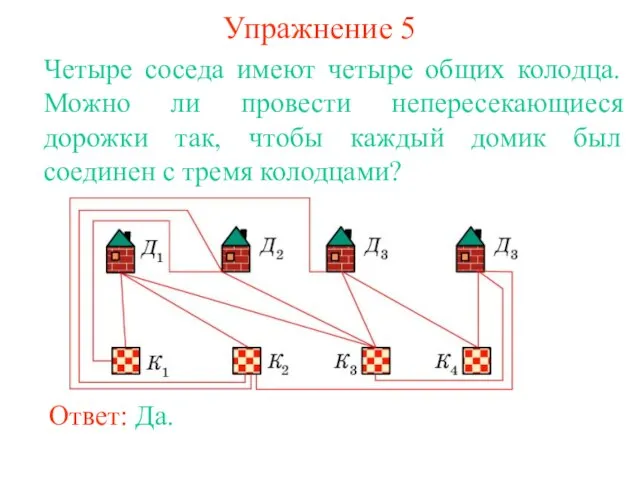
 Фехтование. Спортивное фехтование
Фехтование. Спортивное фехтование Диссидентское движение
Диссидентское движение Акробатика
Акробатика Организация работы с учащимися, имеющими низкую мотивацию к учебно–познавательной деятельности
Организация работы с учащимися, имеющими низкую мотивацию к учебно–познавательной деятельности Государственная (итоговая) аттестация обучающихсяIX, XI классов в 2010/2011 учебном году
Государственная (итоговая) аттестация обучающихсяIX, XI классов в 2010/2011 учебном году Динамика Законы Ньютона
Динамика Законы Ньютона Презентация на тему 2 класс Математический диктант № 1
Презентация на тему 2 класс Математический диктант № 1  Презентация на тему Профессия пожарный
Презентация на тему Профессия пожарный  Бизнес-инжиниринг. Лекция 6
Бизнес-инжиниринг. Лекция 6 Старинные танцы
Старинные танцы Presentation Title Here Subtitle
Presentation Title Here Subtitle  Методы автоматической обработки тем сообщений в потоках новостных сообщений
Методы автоматической обработки тем сообщений в потоках новостных сообщений Биологические особенности ячменя
Биологические особенности ячменя Дисфункция плаценты. Дистресс плода
Дисфункция плаценты. Дистресс плода  Памятники деревянного зодчества в Марийском крае.
Памятники деревянного зодчества в Марийском крае. Будет ли город - сад
Будет ли город - сад атрибуты воинства
атрибуты воинства Ремонтно-реставрационные работы с приспособлением здания ГБУК г. Москвы МДТ им. А.С. Пушкина
Ремонтно-реставрационные работы с приспособлением здания ГБУК г. Москвы МДТ им. А.С. Пушкина Бесплатное продвижение возможно, или внутренняя оптимизация сайта.
Бесплатное продвижение возможно, или внутренняя оптимизация сайта. Номинация «Окружающий мир» (Природоведение) Серые вороны в городе Наблюдение за строительством гнезда
Номинация «Окружающий мир» (Природоведение) Серые вороны в городе Наблюдение за строительством гнезда Г. А. Цукерман, К. Н. Поливанова
Г. А. Цукерман, К. Н. Поливанова К юбилею книги Марка Твена «Приключения Тома Сойера» (1876 год)
К юбилею книги Марка Твена «Приключения Тома Сойера» (1876 год)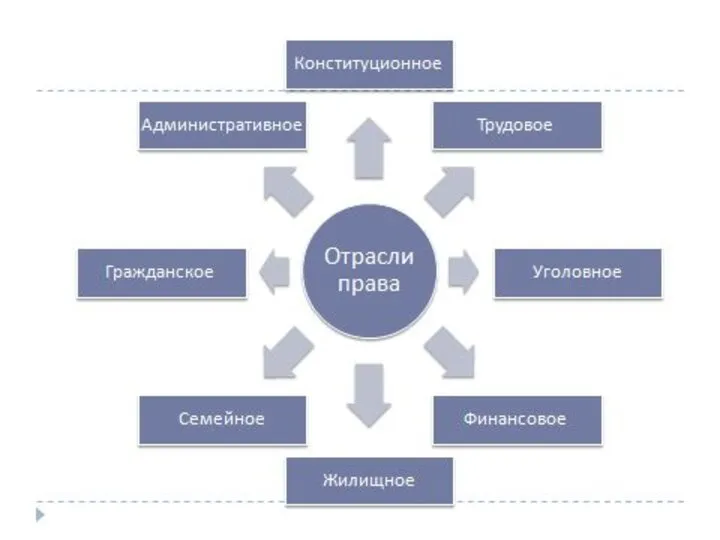 Административное право
Административное право Тема урока
Тема урока Схема установки и принцип работы встроенного таймера электричества
Схема установки и принцип работы встроенного таймера электричества Белоснежка и гномы
Белоснежка и гномы 1 9 9 8
1 9 9 8 Отблески фронтовых пожаров
Отблески фронтовых пожаров