Содержание
- 2. Nuclear Physics Lectures Cross-Sections Why concept is important Learn about dynamics of interaction and/or constituents (cf
- 3. Nuclear Physics Lectures Definition of σ a+b?x Effective area for reaction to occur is σ Beam
- 4. Nuclear Physics Lectures Reaction Rates Na beam particles/unit volume, speed v Flux F= Na v Rate/target
- 5. Nuclear Physics Lectures Breit-Wigner Line Shape Start with NR Schrödinger equation: X by φ*n and integrate
- 6. Nuclear Physics Lectures Breit-Wigner Line Shape - 2 For
- 7. Nuclear Physics Lectures Breit-Wigner Line Shape -3 Normalised Breit-Wigner line shape Q: where have you seen
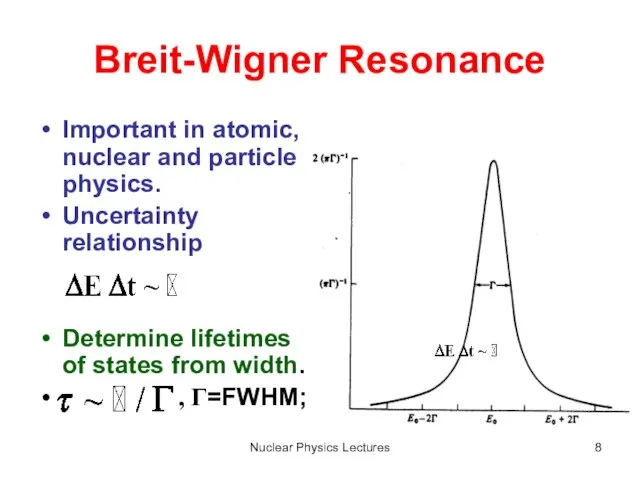
- 8. Nuclear Physics Lectures Breit-Wigner Resonance Important in atomic, nuclear and particle physics. Uncertainty relationship Determine lifetimes
- 9. Nuclear Physics Lectures Fermi Golden Rule Want to be able to calculate reaction rates in terms
- 10. Nuclear Physics Lectures Discrete ? Continuum Decays to a channel i (range of states n). Density
- 11. Nuclear Physics Lectures Cross Section Breit Wigner cross section. Definition of σ and flux F:
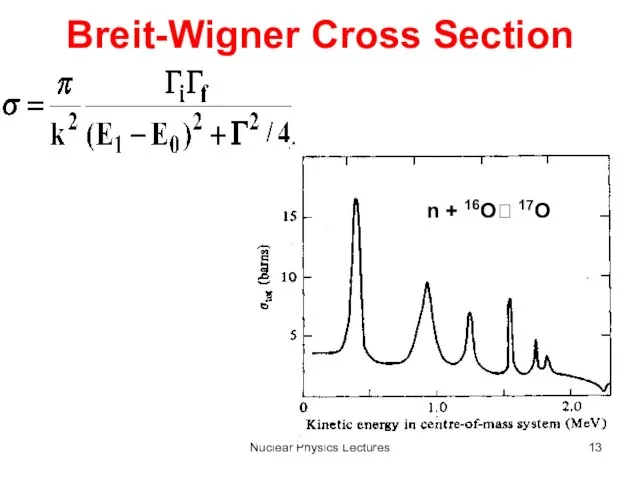
- 12. Nuclear Physics Lectures Breit-Wigner Cross Section Combine rate, flux & density states ?
- 13. Nuclear Physics Lectures Breit-Wigner Cross Section n + 16O? 17O
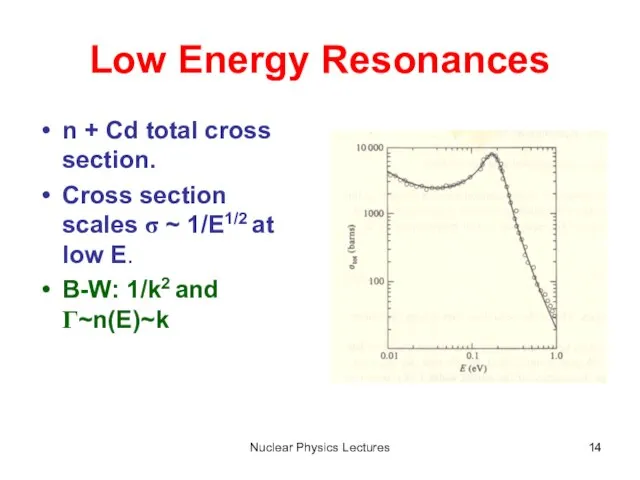
- 14. Nuclear Physics Lectures Low Energy Resonances n + Cd total cross section. Cross section scales σ
- 15. Nuclear Physics Lectures Rutherford Scattering 1
- 16. Nuclear Physics Lectures Rutherford Scattering 2
- 17. Nuclear Physics Lectures Rutherford Scattering 3 Fermi Golden Rule:
- 18. Nuclear Physics Lectures Rutherford Scattering 4 Compare with experimental data at low energy Q: what changes
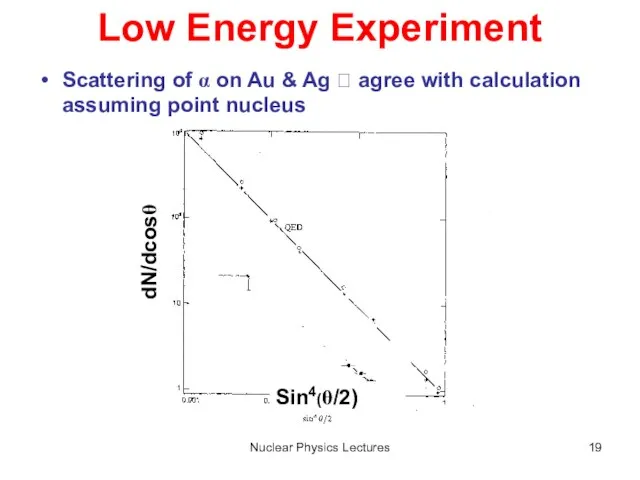
- 19. Nuclear Physics Lectures Low Energy Experiment Scattering of α on Au & Ag ? agree with
- 21. Скачать презентацию














 Политическая сфера. Функции государства
Политическая сфера. Функции государства Римский скульптурный портрет
Римский скульптурный портрет Теоретические основы проектирования методов и технологий обучения
Теоретические основы проектирования методов и технологий обучения Контрактная система
Контрактная система  Презентация на тему Правописание гласных в корне слова
Презентация на тему Правописание гласных в корне слова Презентация на тему Колумбия
Презентация на тему Колумбия Образование в годы войны
Образование в годы войны Профессиональное обучение и дополнительное профессиональное образование
Профессиональное обучение и дополнительное профессиональное образование Антуан Де Сент- Екзюпери Маленький принц. Игра Крестики-нолики
Антуан Де Сент- Екзюпери Маленький принц. Игра Крестики-нолики Дорожная карта завершения СМР и ПНР
Дорожная карта завершения СМР и ПНР Презентация-Трофимов-Дмитрий
Презентация-Трофимов-Дмитрий Значение тренировок для укрепления органов дыхания. Дыхательная гимнастика
Значение тренировок для укрепления органов дыхания. Дыхательная гимнастика Реализация программы «Одаренные дети»
Реализация программы «Одаренные дети» Договор мены (бартер) Войнова Анастасия МЭ 082 ДС 01
Договор мены (бартер) Войнова Анастасия МЭ 082 ДС 01 Корпорация FIRST
Корпорация FIRST Конституционное право
Конституционное право Corel Draw
Corel Draw Урок математики
Урок математики Средства индивидуальной защиты
Средства индивидуальной защиты Инсульт 10 класс
Инсульт 10 класс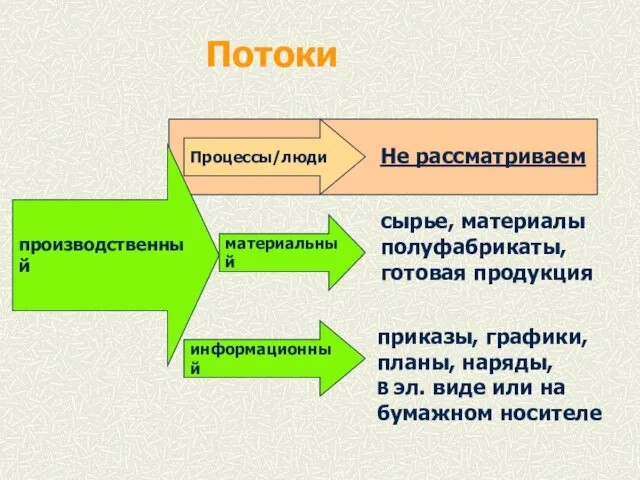 Потоки
Потоки 11.10.2 – Газ природный 40.30.1 – Услуги по поставке водяного пара и горячей воды (включая холодоагенты) 41.00.2 – Услуги по распределени
11.10.2 – Газ природный 40.30.1 – Услуги по поставке водяного пара и горячей воды (включая холодоагенты) 41.00.2 – Услуги по распределени Past Simple - Прошедшее простое время
Past Simple - Прошедшее простое время Индустриалды мәдениет
Индустриалды мәдениет Роль адвокатирования конкуренции в развитии эффективной конкурентной политики
Роль адвокатирования конкуренции в развитии эффективной конкурентной политики Виды тропов и стилистических фигур
Виды тропов и стилистических фигур План развития ЮФО 2020
План развития ЮФО 2020 Международная компания Digital Smart Sistems
Международная компания Digital Smart Sistems