Содержание
- 2. What is search for? Assumptions: single agent, deterministic, fully observable, discrete environment Search for planning The
- 3. Constraint satisfaction problems (CSPs) Definition: State is defined by variables Xi with values from domain Di
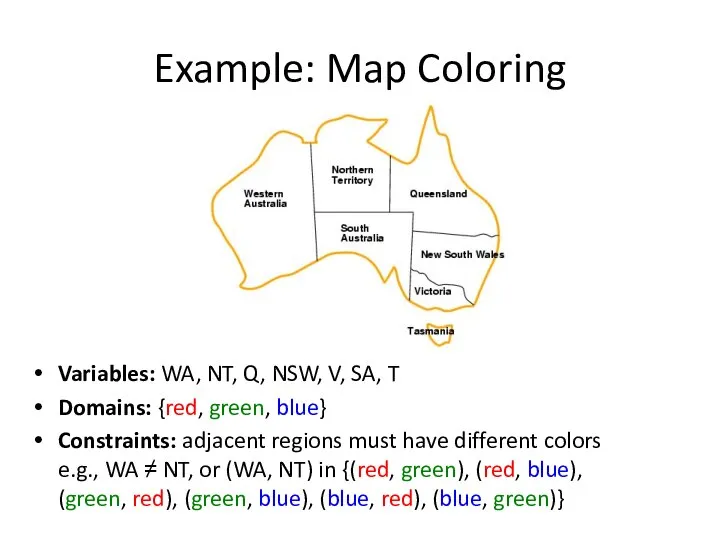
- 4. Example: Map Coloring Variables: WA, NT, Q, NSW, V, SA, T Domains: {red, green, blue} Constraints:
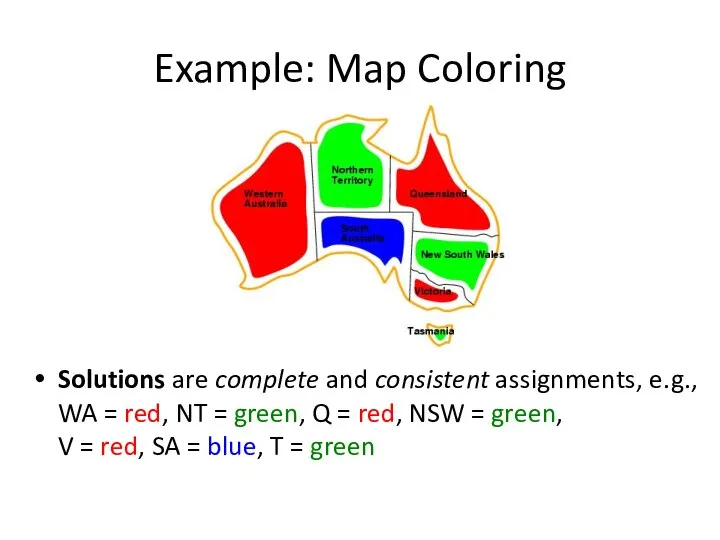
- 5. Example: Map Coloring Solutions are complete and consistent assignments, e.g., WA = red, NT = green,
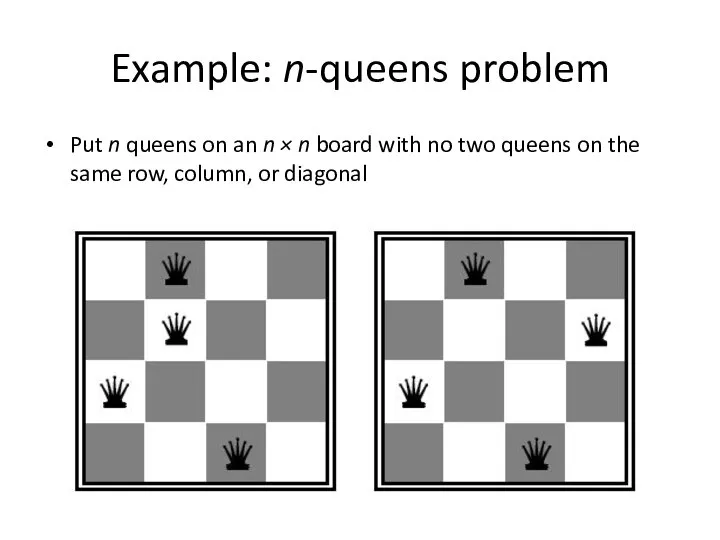
- 6. Example: n-queens problem Put n queens on an n × n board with no two queens
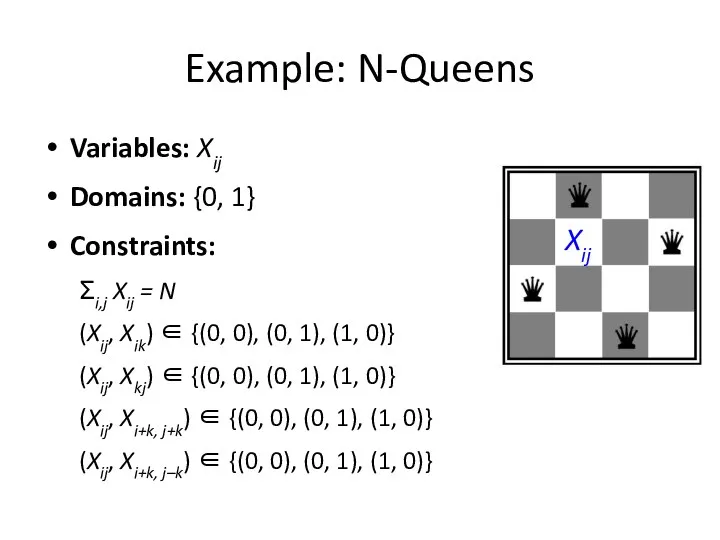
- 7. Example: N-Queens Variables: Xij Domains: {0, 1} Constraints: Σi,j Xij = N (Xij, Xik) ∈ {(0,
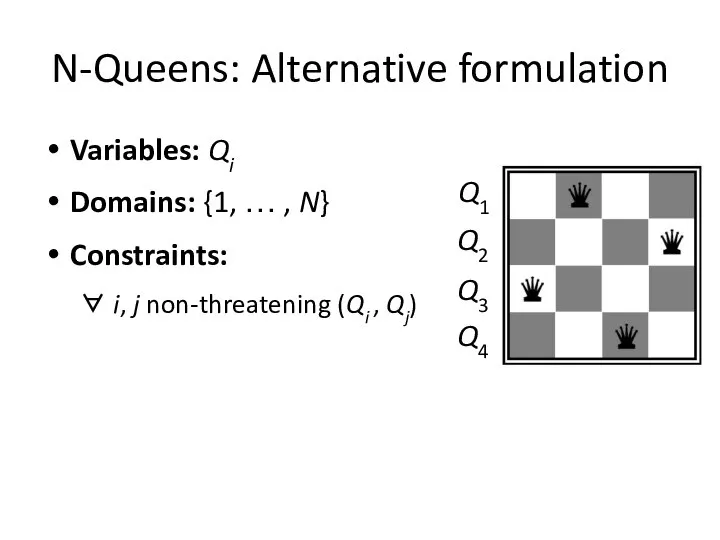
- 8. N-Queens: Alternative formulation Variables: Qi Domains: {1, … , N} Constraints: ∀ i, j non-threatening (Qi
- 9. Example: Cryptarithmetic Variables: T, W, O, F, U, R X1, X2 Domains: {0, 1, 2, …,
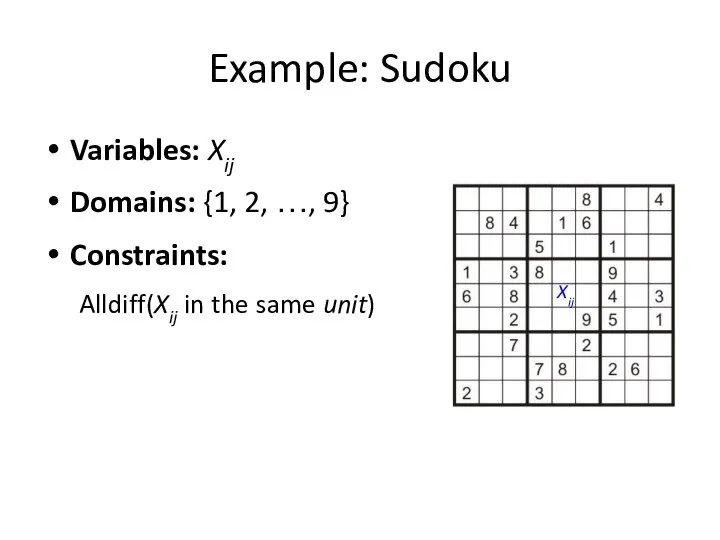
- 10. Example: Sudoku Variables: Xij Domains: {1, 2, …, 9} Constraints: Alldiff(Xij in the same unit) Xij
- 11. Real-world CSPs Assignment problems e.g., who teaches what class Timetable problems e.g., which class is offered
- 12. Standard search formulation (incremental) States: Variables and values assigned so far Initial state: The empty assignment
- 13. Standard search formulation (incremental) What is the depth of any solution (assuming n variables)? n (this
- 14. Backtracking search In CSP’s, variable assignments are commutative For example, [WA = red then NT =
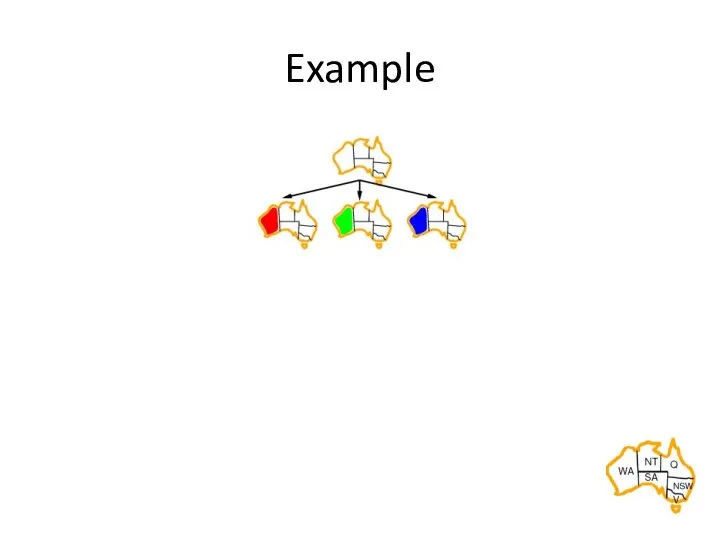
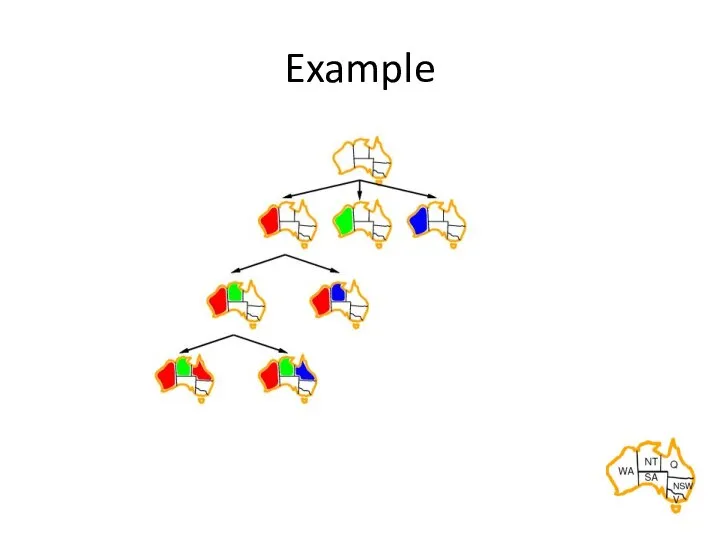
- 15. Example
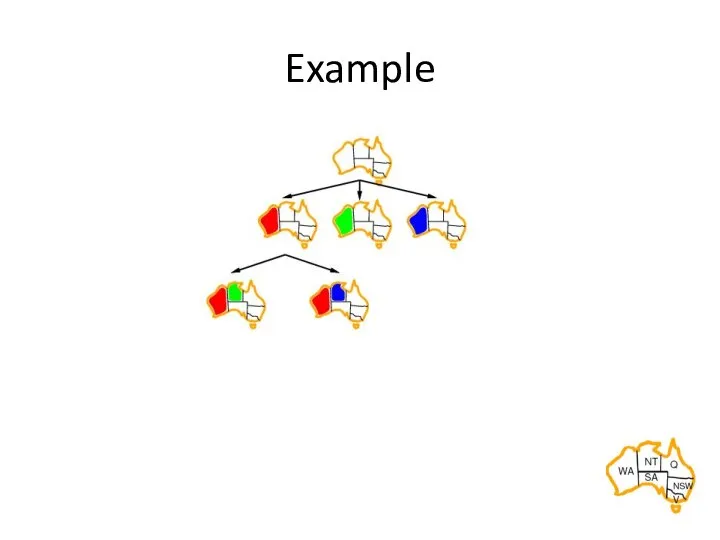
- 16. Example
- 17. Example
- 18. Example
- 19. Backtracking search algorithm Making backtracking search efficient: Which variable should be assigned next? In what order
- 20. Which variable should be assigned next? Most constrained variable: Choose the variable with the fewest legal
- 21. Which variable should be assigned next? Most constrained variable: Choose the variable with the fewest legal
- 22. Which variable should be assigned next? Most constraining variable: Choose the variable that imposes the most
- 23. Which variable should be assigned next? Most constraining variable: Choose the variable that imposes the most
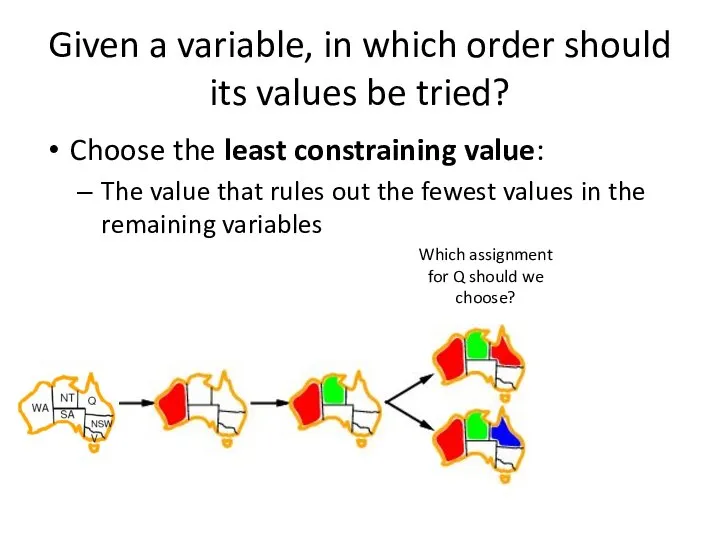
- 24. Given a variable, in which order should its values be tried? Choose the least constraining value:
- 25. Given a variable, in which order should its values be tried? Choose the least constraining value:
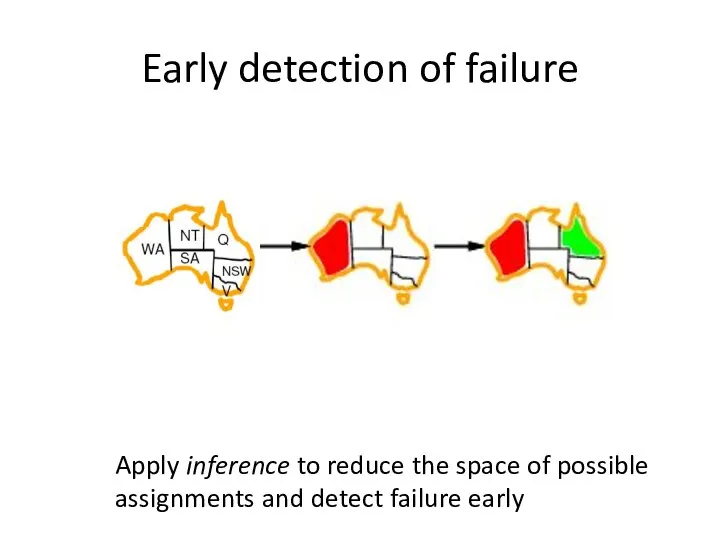
- 26. Early detection of failure Apply inference to reduce the space of possible assignments and detect failure
- 27. Early detection of failure Apply inference to reduce the space of possible assignments and detect failure
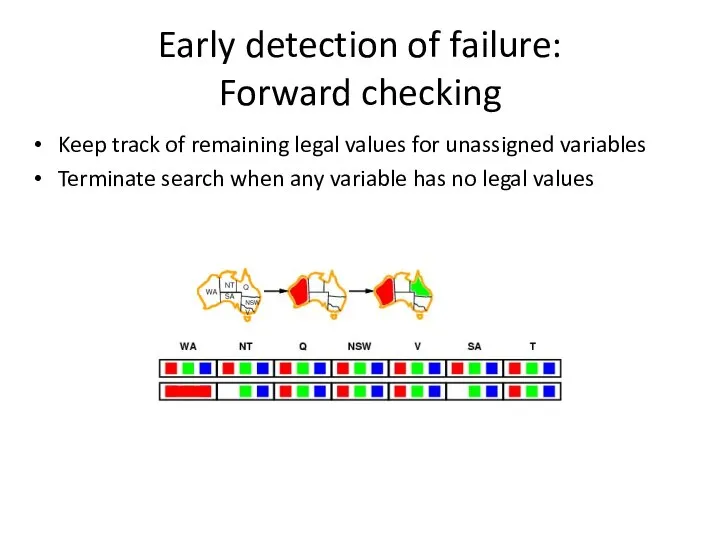
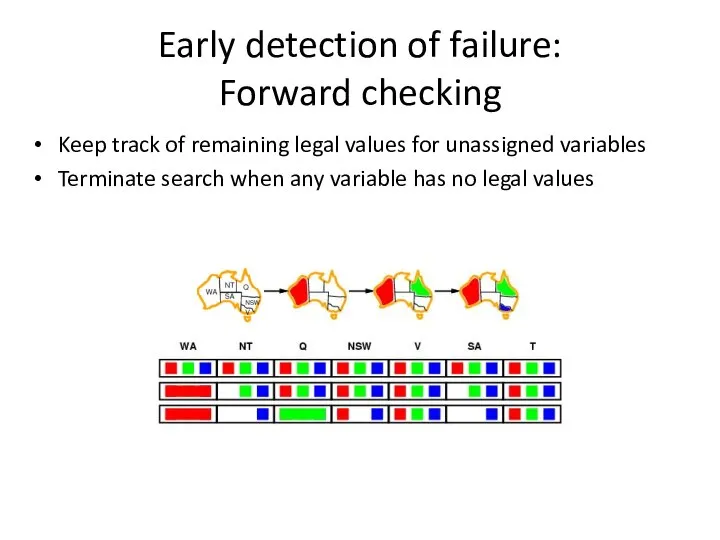
- 28. Early detection of failure: Forward checking Keep track of remaining legal values for unassigned variables Terminate
- 29. Early detection of failure: Forward checking Keep track of remaining legal values for unassigned variables Terminate
- 30. Early detection of failure: Forward checking Keep track of remaining legal values for unassigned variables Terminate
- 31. Early detection of failure: Forward checking Keep track of remaining legal values for unassigned variables Terminate
- 32. Early detection of failure: Forward checking Keep track of remaining legal values for unassigned variables Terminate
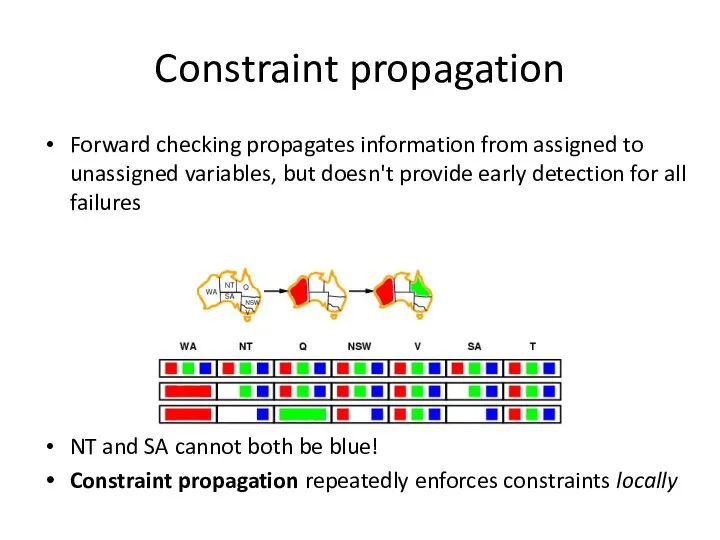
- 33. Constraint propagation Forward checking propagates information from assigned to unassigned variables, but doesn't provide early detection
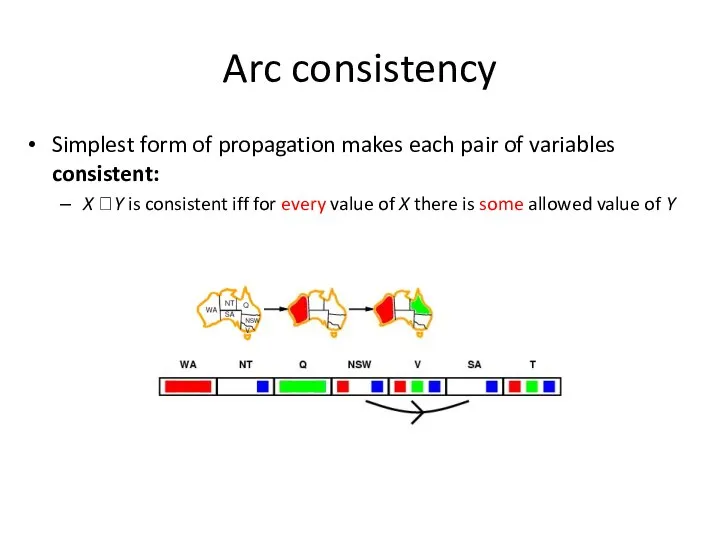
- 34. Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent iff for
- 35. Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent iff for
- 36. Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent iff for
- 37. Arc consistency Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent
- 38. Arc consistency Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent
- 39. Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent iff for
- 40. Simplest form of propagation makes each pair of variables consistent: X ?Y is consistent iff for
- 41. Arc consistency algorithm AC-3
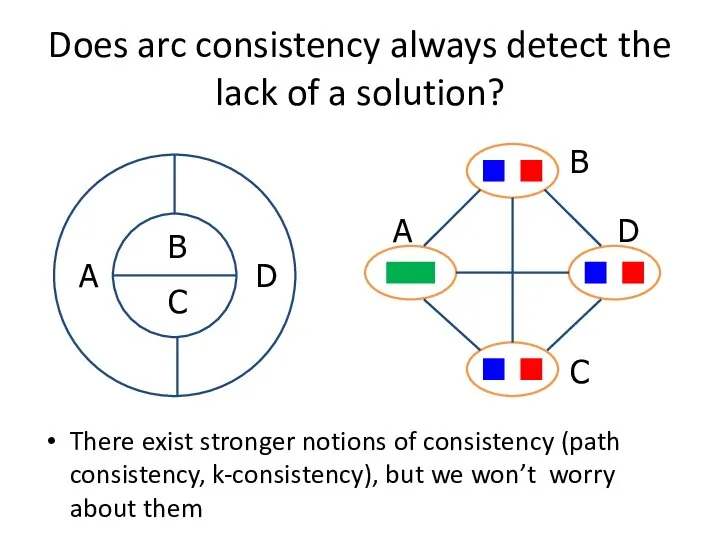
- 42. Does arc consistency always detect the lack of a solution? There exist stronger notions of consistency
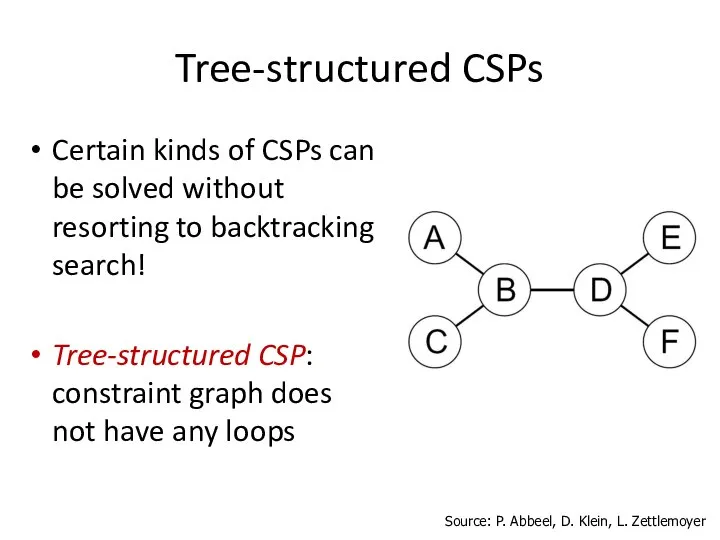
- 43. Tree-structured CSPs Certain kinds of CSPs can be solved without resorting to backtracking search! Tree-structured CSP:
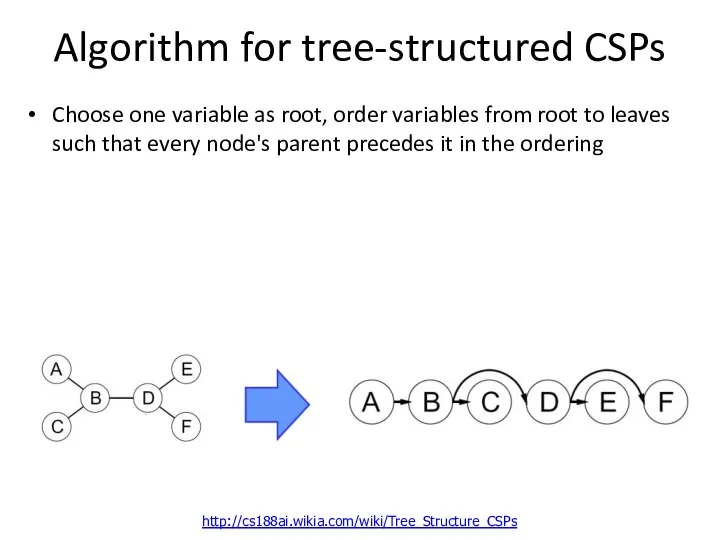
- 44. Algorithm for tree-structured CSPs Choose one variable as root, order variables from root to leaves such
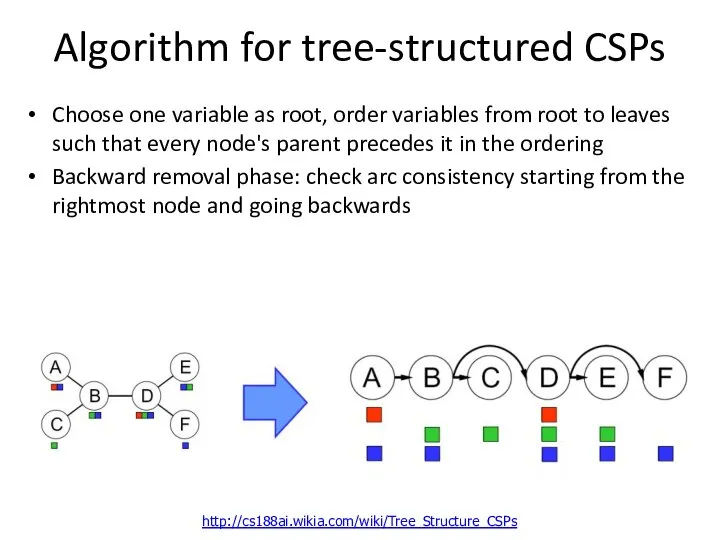
- 45. Algorithm for tree-structured CSPs Choose one variable as root, order variables from root to leaves such
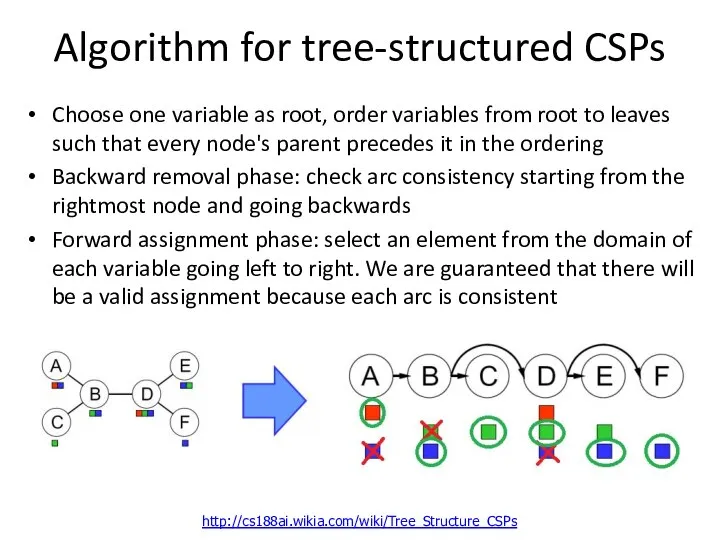
- 46. Algorithm for tree-structured CSPs Choose one variable as root, order variables from root to leaves such
- 47. Algorithm for tree-structured CSPs If n is the numebr of variables and m is the domain
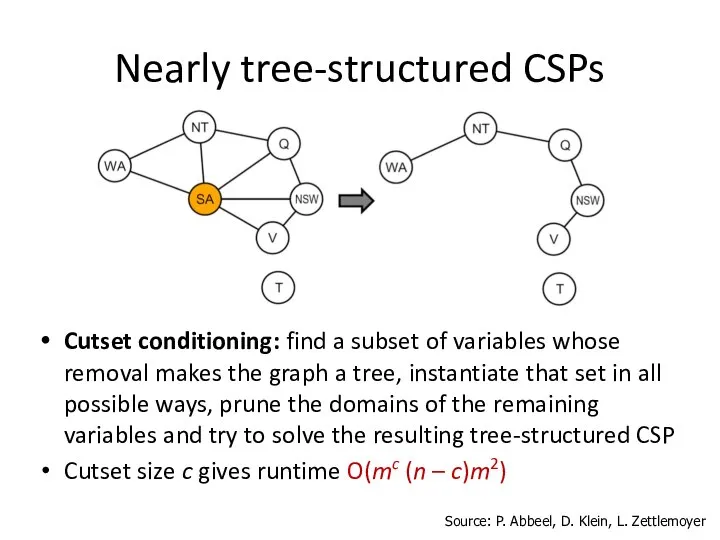
- 48. Nearly tree-structured CSPs Cutset conditioning: find a subset of variables whose removal makes the graph a
- 49. Algorithm for tree-structured CSPs Running time is O(nm2) (n is the number of variables, m is
- 50. Computational complexity of CSPs The satisfiability (SAT) problem: Given a Boolean formula, is there an assignment
- 51. Local search for CSPs Start with “complete” states, i.e., all variables assigned Allow states with unsatisfied
- 52. Local search for CSPs Start with “complete” states, i.e., all variables assigned Allow states with unsatisfied
- 53. Local search for CSPs Start with “complete” states, i.e., all variables assigned Allow states with unsatisfied
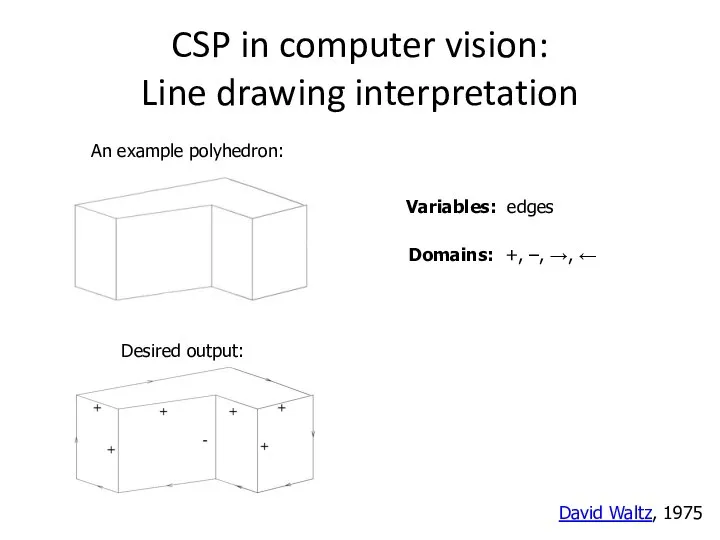
- 54. CSP in computer vision: Line drawing interpretation An example polyhedron: Domains: +, –, →, ← Variables:
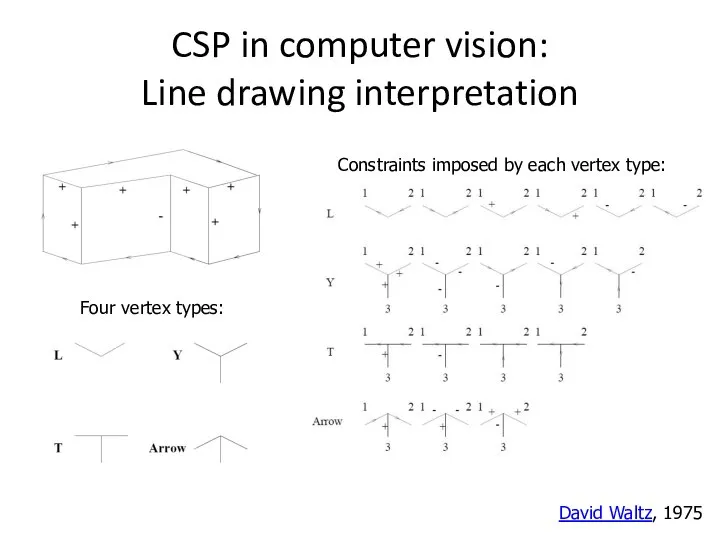
- 55. CSP in computer vision: Line drawing interpretation Four vertex types: Constraints imposed by each vertex type:
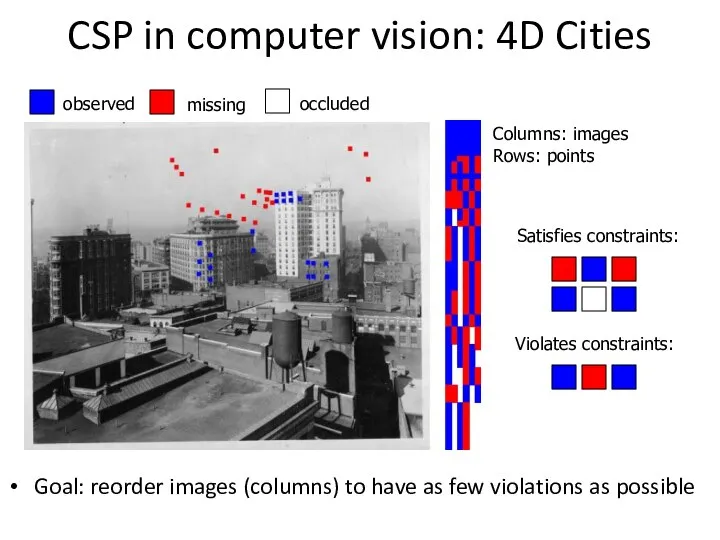
- 56. CSP in computer vision: 4D Cities G. Schindler, F. Dellaert, and S.B. Kang, Inferring Temporal Order
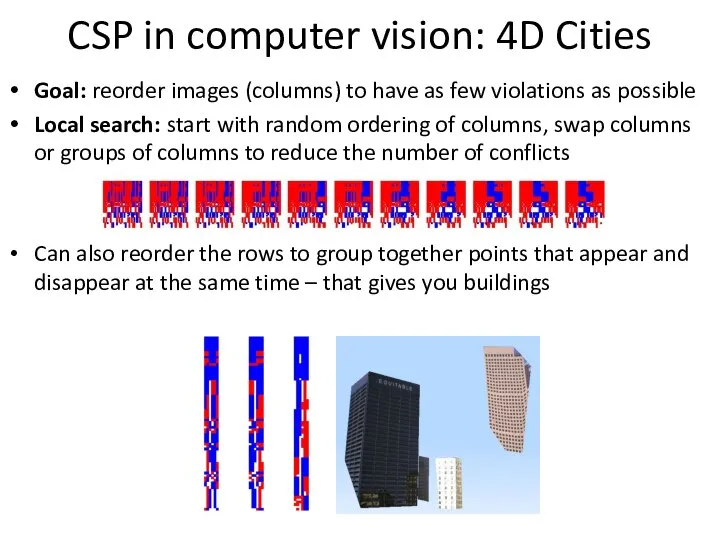
- 57. CSP in computer vision: 4D Cities Goal: reorder images (columns) to have as few violations as
- 58. CSP in computer vision: 4D Cities Goal: reorder images (columns) to have as few violations as
- 60. Скачать презентацию
































 (011)Sensor to bit calculations
(011)Sensor to bit calculations СЕМИНАР по вопросу разработки, представления и регистрации в органах государственного пожарного надзора МЧС России деклараций
СЕМИНАР по вопросу разработки, представления и регистрации в органах государственного пожарного надзора МЧС России деклараций  Презентация на тему Конструирование и моделирование юбок
Презентация на тему Конструирование и моделирование юбок ПРОДВИЖЕНИЕ В ПОИСКОВЫХ СИСТЕМАХ Роскошь или эффективное средство развития бизнеса? Реалии современного Рунета
ПРОДВИЖЕНИЕ В ПОИСКОВЫХ СИСТЕМАХ Роскошь или эффективное средство развития бизнеса? Реалии современного Рунета тема для размышления123321
тема для размышления123321 RedCat SMM paket
RedCat SMM paket Многообразие рыб
Многообразие рыб Городские мотивы в лирике Н.А. Некрасова
Городские мотивы в лирике Н.А. Некрасова Технологии 3D рендера в проектах "Ил-2” и "Второй мировой".
Технологии 3D рендера в проектах "Ил-2” и "Второй мировой". Определение параметров муниципальных услуг
Определение параметров муниципальных услуг Основные направления деятельности студенческих отрядов
Основные направления деятельности студенческих отрядов Наука и образование
Наука и образование Внешняя политика России в 90-е годы
Внешняя политика России в 90-е годы Форматы мясного цеха
Форматы мясного цеха Спортивно-патриотические мероприятие, посвященное Дню защитника Отечества “А ты готов?“
Спортивно-патриотические мероприятие, посвященное Дню защитника Отечества “А ты готов?“ Организация исследовательской деятельности
Организация исследовательской деятельности Сложение и вычитание дробей
Сложение и вычитание дробей FIS Collection System Возврат долгов: от стратегии к задачам.
FIS Collection System Возврат долгов: от стратегии к задачам. Методические рекомендации по работе над творческим проектом
Методические рекомендации по работе над творческим проектом Исполнитель Робот
Исполнитель Робот Обязанности ООК и ООС
Обязанности ООК и ООС Осенние праздники
Осенние праздники Дополнение«Альфа-Авто»: Управление взаимоотношениями с клиентами, редакция 5Для автосалонов
Дополнение«Альфа-Авто»: Управление взаимоотношениями с клиентами, редакция 5Для автосалонов Подвижные игры с элементы баскетбола на уроках в начальной школе
Подвижные игры с элементы баскетбола на уроках в начальной школе Kasbga yo'naltirish trening slayd (5)
Kasbga yo'naltirish trening slayd (5) Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Favourite sports
Презентация на тему Favourite sports Презентация на тему Алкалоиды
Презентация на тему Алкалоиды