Давление в жидкости и газе

Жидкость же, имея определенный объем,
принимает форму того сосуда, в который она заключена. Но в жидкости в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.

Свойства жидкостей и газов во многом отличаются, однако в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями.
Гидроаэромеханика - раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твердыми телами, - использует единый подход к изучению жидкостей и газов.

В механике с большой степенью точности жидкости и газы рассматриваются как сплошные, непрерывно распределенные.
Плотность же газов от давления зависит существенно.
Из опытов известно, что сжимаемостью жидкости и газа можно пренебречь и пользоваться единым понятием
несжимаемой жидкости – жидкости, плотность которой всюду одинакова и не изменяется со временем.

Если в покоящуюся жидкость поместить тонкую
пластинку, то части жидкости, находящиеся по
разные стороны от нее, будут действовать на каждый
ее элемент с силами , которые независимо от того,
как пластинка ориентирована, будут равны по
модулю и направлены перпендикулярно площадке ,
так как наличие касательных сил привело бы частицы
жидкости в движение.

Единица давления – паскаль (Па).
Физическая величина, определяемая нормальной силой,
действующей со стороны жидкости на единицу площади,
называется давлением жидкости
Давление при равновесии жидкостей (газов) подчи-
няется закону Паскаля: давление в любом месте
покоящейся жидкости одинаково по всем направле-
ниям, причем давление одинаково передается по
всему объему, занятому покоящейся жидкостью.

Рассмотрим роль веса жидкости на распределение
давления внутри покоящейся несжимаемой жидкости.
При равновесии жидкости давление по горизонтали
всегда одинаково, иначе не было бы равновесия.
Поэтому свободная поверхность покоящейся жидкости
всегда горизонтальна вдали от стенок сосуда.
Если жидкость несжимаема, то ее плотность не зависит
от давления.
Тогда при поперечном сечении столба жидкости,
его высоте и плотности вес , а
давление на нижнее основание
Давление называется гидростатическим давлением.
(1)

Согласно формуле (1), сила давления на нижние
слои жидкости будет больше, чем на верхние, поэтому
на тело, погруженное в жидкость, действует сила,
определяемая законом Архимеда: на тело, погружен-
ное в жидкость (газ), действует со стороны этой жид-
кости направленная вверх выталкивающая сила,
равная весу вытесненной телом жидкости (газа)
где - плотность жидкости,
- объем погруженного в жидкость тела.

Архимед (287 - 212 до н.э.)
Древнегреческий ученый, математики и изобретатель, родился в Сиракузах

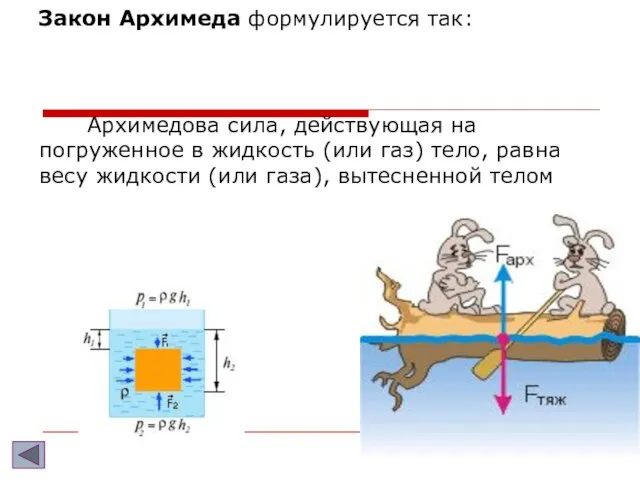
Закон Архимеда формулируется так:
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом

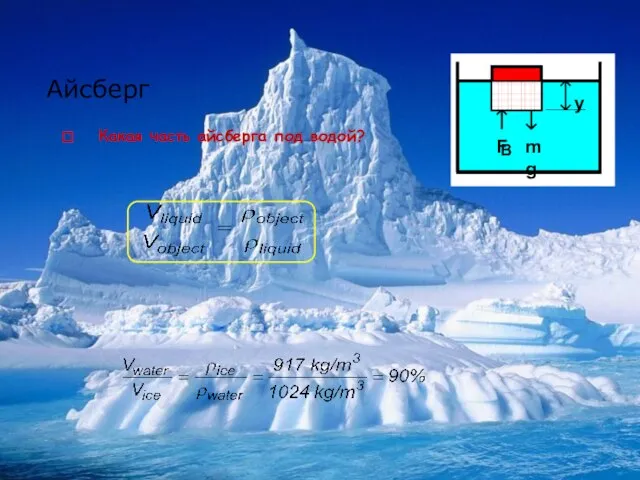
Айсберг
Какая часть айсберга под водой?

Движение жидкостей называется течением.
Совокупность частиц движущейся жидкости - потоком.
Графически движение жидкостей изображается с
помощью линий тока, которые проводятся так, что
касательные к ним совпадают по направлению с
вектором скорости
жидкости в соответ-
ствующих точках
пространства.
УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

Линии тока проводятся так, чтобы густота их,
характеризуемая отношением числа линий к площади
перпендикулярной им площадки, через которую они
проходят, была больше там, где больше скорость
течения жидкости, и меньше там, где жидкость течет
медленнее.
По картине линий тока можно судить о направлении и
модуле скорости в разных точках пространства, т.е.
можно определить состояние
движения жидкости. Линии
тока в жидкости можно
"проявить", например,
подмешав в нее какие-
нибудь заметные
взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока.
Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока,
а также значения скоростей в каждой ее точке со временем не изменяются.

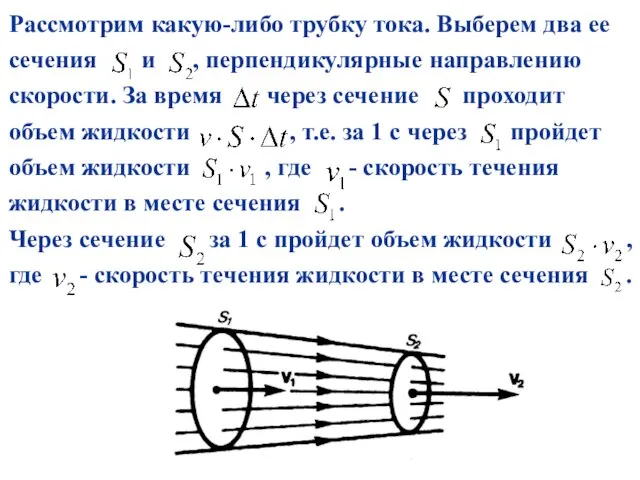
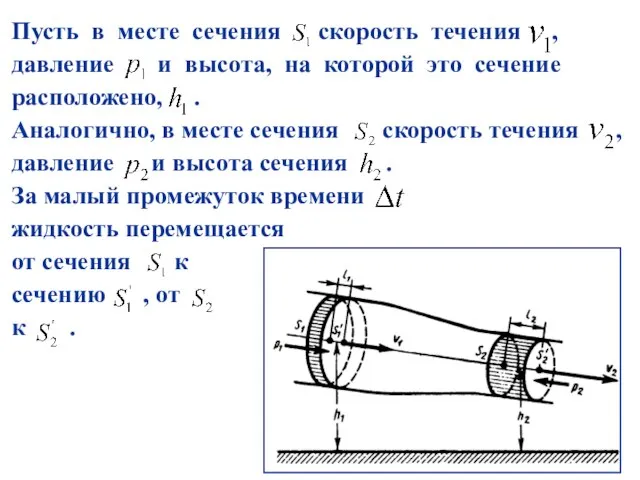
Рассмотрим какую-либо трубку тока. Выберем два ее
сечения и , перпендикулярные направлению
скорости. За время через сечение проходит
объем жидкости , т.е. за 1 с через пройдет
объем жидкости , где - скорость течения
жидкости в месте сечения .
Через сечение за 1 с пройдет объем жидкости ,
где - скорость течения жидкости в месте сечения .

Здесь предполагается, что скорость жидкости в сечении
постоянна. Если жидкость несжимаема ( ), то
через сечение пройдет такой же объем жидкости,
как и через сечение , т.е.
(2)
Следовательно, произведение скорости течения
несжимаемой жидкости на поперечное сечение трубки
тока есть величина постоянная для данной
трубки тока.
Соотношение (2)
называется уравнением
неразрывности для
несжимаемой жидкости.

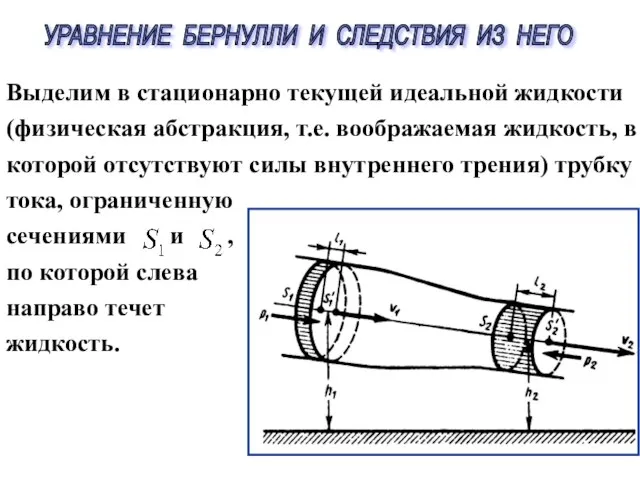
Выделим в стационарно текущей идеальной жидкости
(физическая абстракция, т.е. воображаемая жидкость, в
которой отсутствуют силы внутреннего трения) трубку
тока, ограниченную
сечениями и ,
по которой слева
направо течет
жидкость.
УРАВНЕНИЕ БЕРНУЛЛИ И СЛЕДСТВИЯ ИЗ НЕГО

Пусть в месте сечения скорость течения ,
давление и высота, на которой это сечение
расположено, .
Аналогично, в месте сечения скорость течения ,
давление и высота сечения .
За малый промежуток времени
жидкость перемещается
от сечения к
сечению , от
к .

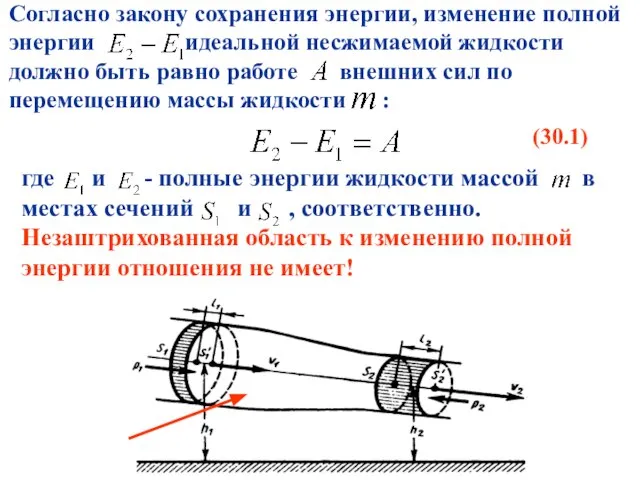
Согласно закону сохранения энергии, изменение полной
энергии идеальной несжимаемой жидкости
должно быть равно работе внешних сил по
перемещению массы жидкости :
(30.1)
где и - полные энергии жидкости массой в
местах сечений и , соответственно.
Незаштрихованная область к изменению полной
энергии отношения не имеет!

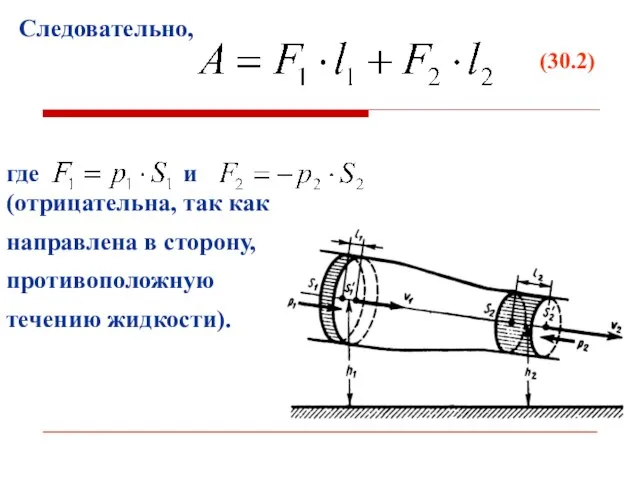
Следовательно,
(30.2)
где и
(отрицательна, так как
направлена в сторону,
противоположную
течению жидкости).

Полные энергии и будут складываться из
кинетической и потенциальной энергий массы
жидкости:
(30.3)
(30.4)
Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1)
и (30.2), получим
(30.5)

Согласно уравнению неразрывности для несжимаемой
жидкости (29.1), объем, занимаемый жидкостью,
остается постоянным, т.е. .
Разделив выражение (30.5) на , получим
где - плотность жидкости.
Так как сечения выбирались произвольно, то можно
записать
(30.6)

Выражение (30.6) называется уравнением Бернулли.
Оно представляет собой закон сохранение энергии
применительно к установившемуся течению
идеальной жидкости. Оно хорошо выполняется и для
реальных жидкостей, внутреннее трение которых
не очень велико.
Величина в формуле (30.6) называется статическим
давлением (давление жидкости на поверхность
обтекаемого ею тела).
Величина - динамическое давление.
Величина - гидростатическое давление.

Для горизонтальной трубки тока ( )
выражение (30.6) принимает вид
(30.7)
где называется полным давлением.

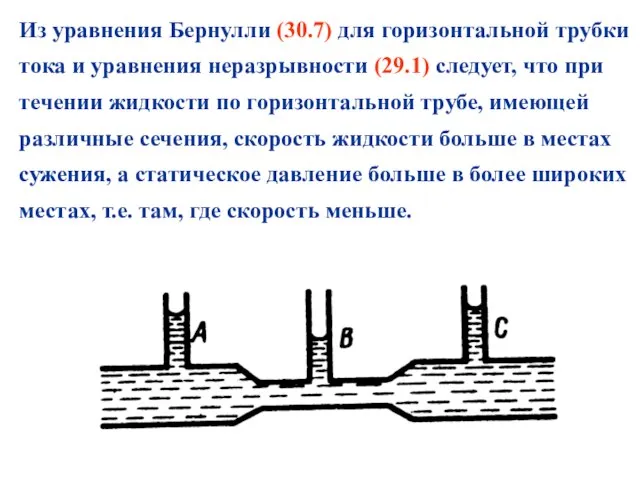
Из уравнения Бернулли (30.7) для горизонтальной трубки
тока и уравнения неразрывности (29.1) следует, что при
течении жидкости по горизонтальной трубе, имеющей
различные сечения, скорость жидкости больше в местах
сужения, а статическое давление больше в более широких
местах, т.е. там, где скорость меньше.

Вязкость (внутреннее трение) - это свойство реальных
жидкостей оказывать сопротивление перемещению
одной части жидкости относительно другой.
При перемещении одних слоев реальной жидкости
относительно других возникают силы внутреннего
трения, направленные по касательной к поверхности
слоев. Действие этих сил проявляется в том, что со
стороны слоя, движущегося быстрее, на слой,
движущийся медленнее, действует ускоряющая сила.
Со стороны же слоя, движущегося медленнее, на слой,
движущийся быстрее, действует тормозящая сила.
ВЯЗКОСТЬ (ВНУТРЕННЕЕ ТРЕНИЕ). ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ.

Сила внутреннего трения тем больше, чем больше
рассматриваемая площадь поверхности слоя , и
зависит от того, насколько быстро меняется скорость
течения жидкости при переходе от слоя к слою.
На рисунке представлены два слоя, отстоящие друг
от друга на расстоянии и движущиеся со
скоростями и .
При этом .
Направление, в котором
отсчитывается расстояние
между слоями, перпенди-
кулярно скорости течения
слоев.

Величина показывает, как быстро меняется
скорость при переходе от слоя к слою в направлении ,
перпендикулярном направлению движения слоев, и
называется градиентом скорости.
Таким образом, модуль силы внутреннего трения
(31.1)
где коэффициент пропор-
циональности , завися-
щий от природы жидкости,
называется динамической
вязкостью (или просто
вязкостью).
Единица вязкости - Па.с.

Чем больше вязкость, тем сильнее жидкость отличается
от идеальной, тем большие силы внутреннего трения в
ней возникают.
Вязкость зависит от температуры, причем характер этой
зависимости для жидкостей и газов различен.
Для жидкостей с увеличением температуры вязкость
уменьшается, у газов, наоборот, увеличивается.
Данный факт указывает на различие в них механизмов
внутреннего трения.
Особенно сильно зависит от температуры вязкость масел.

Существует два режима течения жидкостей. Течение
называется ламинарным (слоистым), если вдоль
потока каждый выделенный тонкий слой скользит
относительно соседних, не перемешиваясь с ними,
и турбулентным (вихревым), если вдоль потока
происходит интенсивное вихреобразование и
перемешивание жидкости (газа).

Ламинарное течение жидкости наблюдается при
небольших скоростях ее движения. Внешний слой
жидкости, примыкающий к поверхности трубы, в
которой она течет, из-за сил молекулярного сцепления
прилипает к ней и остается неподвижным. Скорости
последующих слоев тем больше, чем больше их
расстояние от поверхности трубы, и наибольшей
скоростью обладает слой, движущийся вдоль оси трубы.

При турбулентном течении частицы жидкости
приобретают составляющие скорости, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой.
Скорость частиц жидкости быстро возрастает по мере
удаления от поверхности трубы, затем изменяется
довольно незначительно. Так как частицы жидкости
переходят из одного слоя в другой, то их скорости в
различных слоях мало отличаются. Из-за большого
градиента скоростей у поверхности трубы обычно
происходит образование вихрей.

Turbulent flow in a jet
Turbulence is associated with intense mixing and unsteady flow.

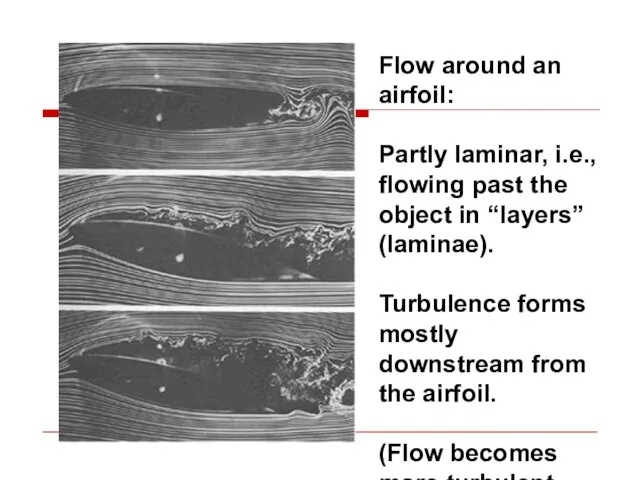
Flow around an airfoil:
Partly laminar, i.e., flowing past the object in “layers” (laminae).
Turbulence forms mostly downstream from the airfoil.
(Flow becomes more turbulent with increased angle of attack.)

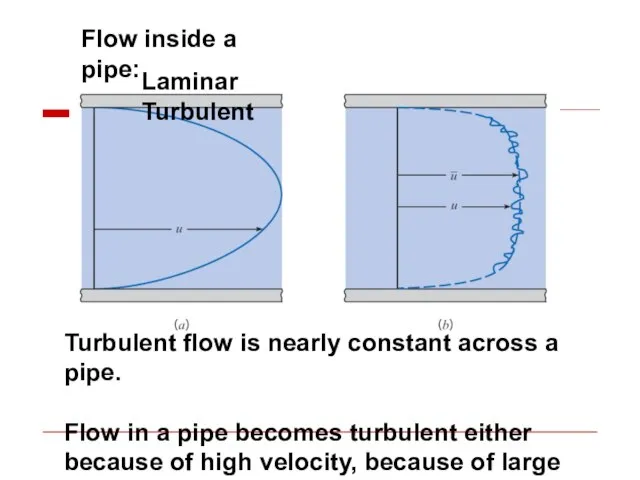
Flow inside a pipe:
Laminar Turbulent
Turbulent flow is nearly constant across a pipe.
Flow in a pipe becomes turbulent either because of high velocity, because of large pipe diameter, or because of low viscosity.

Профиль усредненной скорости при турбулентном
течении в трубах отличается от параболического
профиля при ламинарном течении более быстрым
возрастанием скорости у стенок трубы и меньшей
кривизной в центральной части течения. Характер
течения зависит от безразмерной величины,
называемой числом Рейнольдса

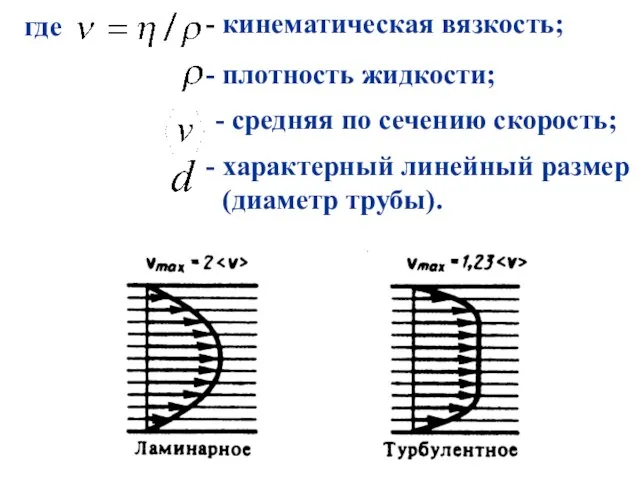
где
кинематическая вязкость;
плотность жидкости;
- средняя по сечению скорость;
характерный линейный размер (диаметр трубы).