Информатика

Слайд 2
Логические основы построения цифровых автоматов
Основные законы и постулаты цифровых автоматов
2. Представление функций алгебры логики
3. Логический синтез переключательных и вычислительных схем
3.1. Синтез переключательных схем
3.2. Синтез вычислительных схем
4. Основы элементной базы цифровых автоматов
4.1.Логические элементы
4.2 Схемотехника логических элементов
4.3 Элементы интегральных схем
Контрольные вопросы

Слово логика означает совокупность правил, которым подчиняется процесс мышления.
Сам термин "логика" происходит от древнегреческого logos, означающего "слово, мысль, понятие, рассуждение, закон". Формальная логика - наука о формах и законах мышления. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика как наука позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления являются понятия, суждения и умозаключения.
Понятие - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других. Например, компьютер, человек, ученики.
Суждения - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета и которая может быть либо истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение. Вопросительные и побудительные предложения суждениями не являются
Логические основы построения цифровых автоматов
Слайд 3

Слайд 4
Суждения рассматриваются не с точки зрения их смысла и содержания, а только с точки зрения их истинности или ложности. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных объектов. "Дважды два равно четырем" - истинное суждение, а вот "Процессор предназначен для печати" - ложное. Суждения могут быть простыми и сложными. "Весна наступила, и грачи прилетели" - сложное суждение, состоящее из двух простых. Простые суждения (высказывания) выражают связь двух понятий. Сложные - состоят из нескольких простых суждений.
Умозаключение - прием мышления, позволяющий на основе одного или нескольких суждений-посылок получить новое суждение (знание или вывод).
Примерами умозаключений являются доказательства теорем в геометрии. Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда и умозаключение будет истинным. Иначе можно прийти к ложному умозаключению
Логические основы построения цифровых автоматов

Слайд 5
Логические основы построения цифровых автоматов
Алгебра логики. История логики
Алгебра — раздел математики, исследующий операции, аналогичные сложению, умножению, вычитанию и делению и выполняемые не только над числами, но и над другими математическими объектами, например, многочленами, векторами, матрицами, операторами и т.д., над объектами самой различной природы.
Возникла алгебра в связи с поисками общих приемов решения однотипных арифметических задач. В основе найденных алгеброй общих приемов лежат действия над величинами (составление и решение уравнений), выраженных буквами, независимо от их конкретного числового значения. Введение символики имело исключительное значение и явилось огромным шагом вперед в развитии математики, так как введение буквенных обозначений сделало запись сжатой и удобной для построения исчислений. Применение буквенных обозначений облегчило и исследование общих свойств числовых систем и общих методов решения задач при помощи уравнений.

Слайд 6
Логические основы построения цифровых автоматов
Как грамматика изучает формы отдельного слова и формы сочетания слов в предложении, отвлекаясь от конкретного содержания языковых выражений; как математика рассматривает количественные и пространственные отношения и формы, отвлекаясь от конкретных материальных предметов, так и формальная логика исследует формы отдельных мыслей и формы сочетаний их в отвлечении от конкретного содержания суждений, умозаключений, доказательств и понятий. Составной частью формальной логики является математическая логика.
Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера. Суждения в математической логике называют высказываниями или логическими выражениями. Подобно тому, как для описания действий над переменными был разработан раздел математики алгебра, так и для обработки логических выражений в математической логике была создана алгебра высказываний, или алгебра логики.

Слайд 7
Зародилась логика в лоне единой нерасчлененной науки — античной философии, которая тогда объединяла всю совокупность знаний о мире и о самом человеке и его мышлении. В IV в. до н. э. логика начинает развиваться под влиянием возросшего интереса к ораторскому искусству. Это характерно не только для Древней Греции, но и для Древней Индии, Древнего Китая, Древнего Рима и феодальной России.
Как известно, в первом сочинении Аристотеля (384 — 322 до н. э.) по логике проблемы логики рассматривались в связи с теорией ораторского искусства.
Декарт Рене (1596-1650, фр. философ, математик) предложил в логике использовать математические методы.

Слайд 8
Первый русский фундаментальный труд по логике, написанный М.В. Ломоносовым (1711 — 1765), называется «Краткое руководство к красноречию».
Основы математической логики заложил немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646 — 1716). Он сделал попытку построить первые логические исчисления, считал, что можно заменить простые рассуждения действиями со знаками и привел соответствующие правила.
Но Лейбниц высказал только идею, а развил ее окончательно англичанин Джордж Буль (1815 — 1864). Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Недаром начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.

Слайд 9
Алгебра логики – раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Приведем еще одно определение алгебры логики, устанавливающее связь с высказыванием.
Алгебра логики (логика высказываний) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях высказываний.
Попробуем разобраться что же такое логическое высказывание?

Слайд10
Или же
Высказывания

Слайд 11
ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

Рассмотрим основные законы алгебры логики.
1. Переместительный закон (закон коммутативности) для логического умножения и логического сложения: a·b = b·a; a+b = b+a.
2. Сочетательный закон (закон ассоциативности) для логического умножения и логического сложения: (a·b)·c = a·(b·c); (a+b)+c = a+(b+c).
3. Распределительный закон (дистрибутивный закон): a+b·c=(a+b)(a+c);
(b+c)·a=a·b+a·c;
a+b·c=(a·1+b·c)=a·(1+b+c)+b·c = a·a+a·b+a·c+b·c=a·(a+b)+c·(a+b)=
= (a+b)·(a+c).
4. Закон поглощения: a+a·b=a·(1+b)=a; a·(a+b)=a·a+a·b=a.
Слайд 12

Слайд 13

Слайд 14

Слайд 15
Законы 1 – 10 свидетельствуют о том, что алгебра логики обладает свойством двойственности (дуальности) относительно операций логического сложения и умножения. Двойственность определяется как изменение всех знаков операций И на знаки операций ИЛИ или всех знаков операций ИЛИ на знаки операций И.
Логическую функцию для удобства записи и последующего синтеза выражают в виде суммы произведений переменных или в виде произведений их сумм. Первая запись называется дизъюнктивной нормальной формой (ДНФ), вторая - конъюнктивной нормальной формой (КНФ).
Дизъюнктивная нормальная форма это запись логической функции в виде суммы произведений переменных.
Конъюнктивная нормальная форма это запись логической функции в виде произведения сумм переменных.

Слайд 16
Для каждой логической функции может существовать несколько равносильных дизъюнктивных и конъюнктивных форм, однако существует только один вид ДНФ или КНФ, в котором функция может быть записана единственным образом (совершенные нормальные формы СДНФ и СКНФ). В СДНФ функция записывается в виде логической суммы конституент единицы (минтермов), а в СКНФ - в виде логического произведения конституент нуля (макстермов).
Конституенты единицы и нуля - это комбинации переменных, при которых функция соответственно обращается в единицу или нуль.

Слайд 17
Минтермом (или элементарной конъюнкцией Qi, или конституентой единицы) называется логическое произведение прямых или инверсных переменных, причем каждая переменная в произведении встречается только один раз:
Макстермом (или элементарной дизъюнкцией Di, или конституентой нуля) называется логическая сумма прямых или инверсных переменных, причем каждая переменная встречается в сумме только один раз:
Количество минтермов и макстермов заданного числа аргументов совпадает с числом различных наборов аргументов N = 2n.

Слайд 18
1. Между индексами і одноименных минтермов и макстермов булевых n переменных существуют следующие соотношения:
где индекс i – десятичное число и соответствует двоичному коду, отвечающему комбинации значений аргументов функции.
2. Логическая сумма всех минтермов любого числа переменных равна единице, т.е.
3. Логическое произведение всех макстермов любого числа переменных равно нулю, т.е.

Слайд 19
4. Логическое произведение минтермов, имеющих разные индексы, равно нулю, т.e: Qi·Qj=0, при i ? j.
5. Логическая сумма неодинаковых макстермов равна единице, т.е. Di+Dj=1, при i ? j.
Для построения СДНФ логической функции FCDHФ от n переменных, заданной таблицей истинности, необходимо по каждому набору переменных, на котором функция принимает значение 1, записать конъюнкцию – минтерм вида
и все такие конъюнкции соединить знаками дизъюнкции. При этом переменные, имеющие значение нуля, инвертируются
где i – десятичные числа, соответствующие тем наборам аргументов, на которых F=Fi=1.

Слайд 20
Для построения СКНФ логической функции FCКHФ от n переменных, заданной таблицей истинности, необходимо по каждому набору переменных, на котором функция принимает значение 0, записать дизъюнкцию – макстерм вида
и все такие дизъюнкции соединить знаками конъюнкции. При этом переменные, имеющие значение единицы, инвертируются:
где i – десятичные числа, соответствующие тем наборам аргументов, на которых F=Fi=0.
Для уменьшения числа логических элементов, реализующих функцию, применяются различные методы минимизации. Под минимизацией логической функции понимают нахождение наиболее простого ее представления в виде суперпозиции операций, составляющих какую-либо фиксированную, функционально полную систему.

Слайд 21
Логическая функция может быть упрощена непосредственно алгебраическим преобразованием с помощью законов алгебры логики (склеивания и поглощения). Но, как правило, такие преобразования требуют громоздких выкладок, а также знаний и навыков. Для функций, имеющих большое число переменных (больше трех) и большое число слагаемых, существуют специальные методы. Наиболее часто применяют методы с использованием карт Вейча и карт Карно, представляющим собой прямоугольную таблицу с числом клеток 2n. Каждой строке (столбцу) этой таблицы соответствует определенная комбинация аргументов (переменных), каждая клетка соответствует определенному набору значений аргументов так, что при всяком переходе из одной клетки в соседнюю вдоль строки или столбца изменяется значение лишь одного аргумента функции. Карты Карно отличаются от диаграмм Вейча порядком расположения аргументов, перечисляемых в циклическом коде (коде Грея) двоичных чисел.

Слайд 22
Алгоритм минимизации логической функции состоит из следующих этапов:
1. Логическую функцию следует привести к СДНФ (СКНФ). Для этого необходимо воспользоваться законами алгебры логики 2, 3, 7-10, а в каждый из членов функции, в которых отсутствуют аргументы, ввести выражение вида
и воспользоваться равенством
для СДНФ
для СКНФ),
где i - отсутствующий в члене аргумент.
2. Заполнить минтермами (макстермами) прямоугольную таблицу, количество клеток которой равно числу возможных минтермов 2n. Минтермы логической функции отмечаются 1 в соответствующих клетках таблицы, а макстермы - 0. Два минтерма, находящиеся в соседних клетках, могут быть заменены одним логическим произведением, содержащим на одну переменную меньше, на основании законов дистрибутивности, склеивания и сложения (умножения) с 1 и 0. В общем случае наличие единиц (нулей) в 2К соседних клетках позволяет исключить К переменных.
,

Слайд 23
3. В заполненной таблице обводят прямоугольными контурами все единицы (нули). При проведении контуров придерживаются следующих правил: контур должен быть прямоугольным; внутри контура должны быть только клетки, заполненные 1 (0); количество клеток находящихся внутри контура, должно быть целой степенью числа 2, т.е. 1, 2, 4, 8, 16; одни и те же клетки, заполненные 1 (0), могут входить в несколько контуров; самая нижняя и самая верхняя строки таблицы, а также самый левый и самый правый столбцы считаются соседними; контуров должно быть как можно меньше, а сами контуры - как можно большими.
4. Выражение минимальной ДНФ (МДНФ) функции записывается следующим образом. Каждый контур в МДНФ представляется членом, число переменных в котором на K меньше общего n – числа аргументов функции, т.е. равно n – К. Каждый член МДНФ составляет лишь из тех аргументов, которые для соответствующего контура являются общими, т.е. имеют значения без инверсии либо с инверсией. В общем случае функция может иметь несколько минимальных форм, которым соответствуют различные, но равноценные по числу членов МДНФ.

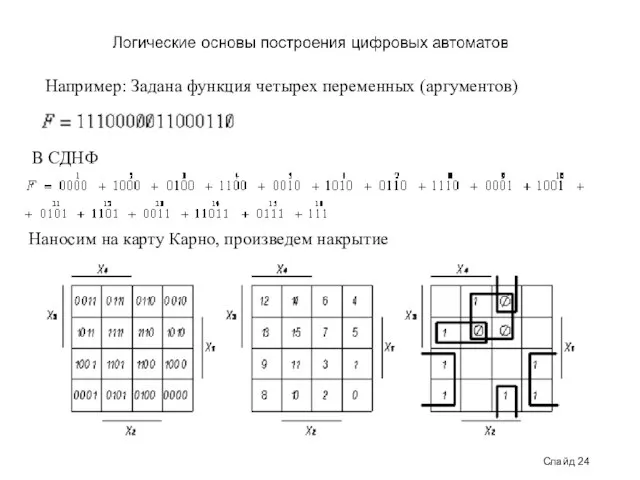
Слайд 24
Например: Задана функция четырех переменных (аргументов)
В СДНФ
Наносим на карту Карно, произведем накрытие

Запишем результат накрытый в виде дезъюнкции конъюнкций (суммы произведений):
Функция до минимизации имела 16 наборов переменных, после четыре.
Слайд 25

Слайд 26
Рассмотрим какая же связь между алгеброй логики и двоичным кодированием?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Логический синтез переключательных и вычислительных схем
Слайд 26

Слайд 27
В каком виде записываются в памяти компьютера и в регистрах процессора данные и команды?
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. Мы уже рассмотрели способы записи двоичной информации на магнитных дисках и на CD-ROM. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:

Слайд 28
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Что такое логический элемент компьютера?

Слайд 29
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рисунке

Слайд 30
Таблица истинности схемы И
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y
(читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.

С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено ниже Знак "1" на схеме — от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
Таблица истинности схемы ИЛИ
Слайд 31

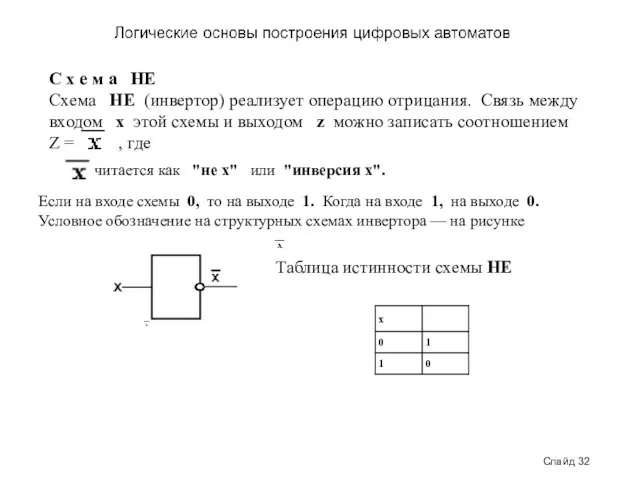
Слайд 32
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением
Z = , где
читается как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке
Таблица истинности схемы НЕ

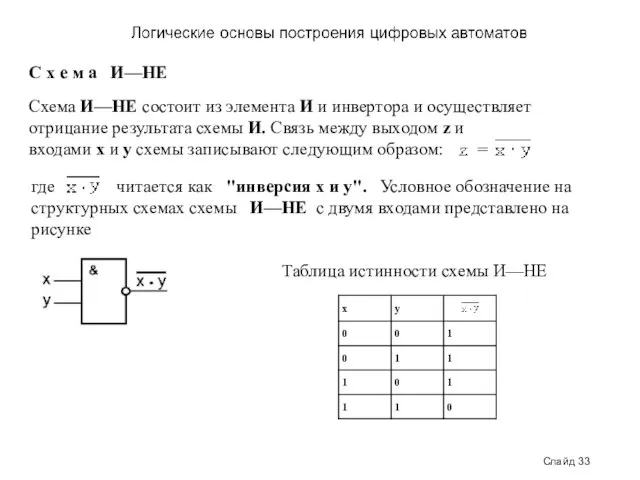
Слайд 33
С х е м а И—НЕ
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:
где читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке
Таблица истинности схемы И—НЕ

Слайд 34
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
где читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рисунке
Таблица истинности схемы ИЛИ—НЕ

Слайд 35
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рисунке.

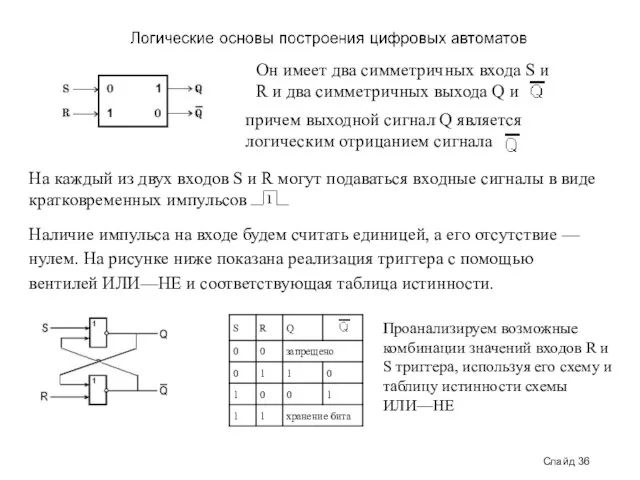
Слайд 36
Он имеет два симметричных входа S и R и два симметричных выхода Q и
причем выходной сигнал Q является логическим отрицанием сигнала
На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем. На рисунке ниже показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ—НЕ

Слайд 37
1. Если на входы триггера подать S=“1”, R=“0”, то (независимо от состояния) на выходе Q верхнего вентиля появится “0”. После этого на входах нижнего вентиля окажется R=“0”, Q=“0” и выход станет равным “1”.
2. Точно так же при подаче “0” на вход S и “1” на вход R на выходе
появится “0”, а на Q — “1”.
3 Если на входы R и S подана логическая “1”, то состояние Q и не меняется.
4. Подача на оба входа R и S логического “0” может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210= 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Слайд 38
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора на рисунке
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:
1. цифра ai первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос pi–1 из младшего разряда.

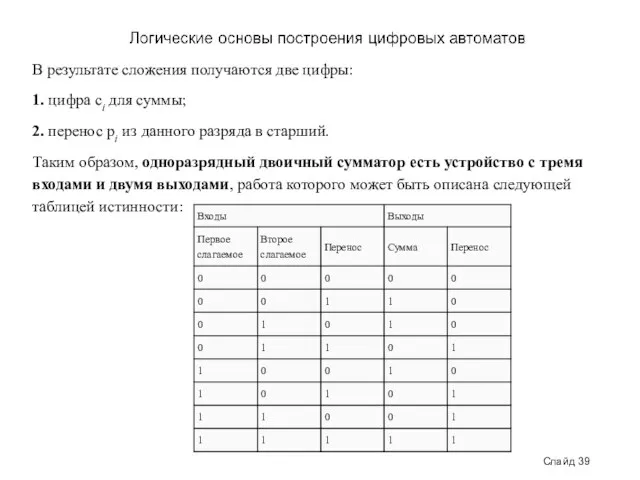
Слайд 39
В результате сложения получаются две цифры:
1. цифра ci для суммы;
2. перенос pi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности: