Содержание
- 2. Properties of Demand Functions Comparative statics analysis of ordinary demand functions -- the study of how
- 3. Own-Price Changes How does x1*(p1,p2,y) change as p1 changes, holding p2 and y constant? Suppose only
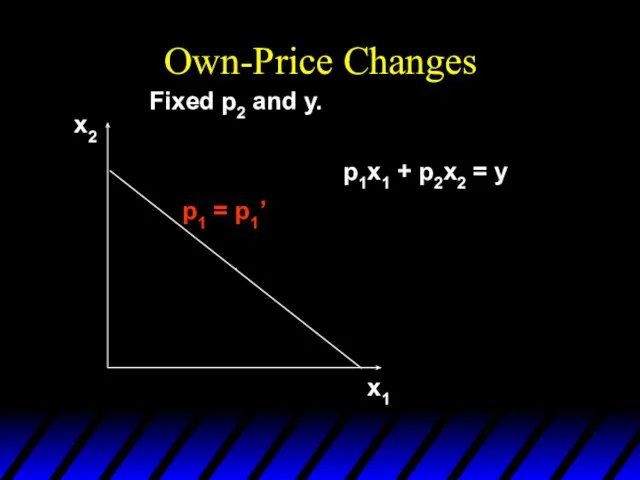
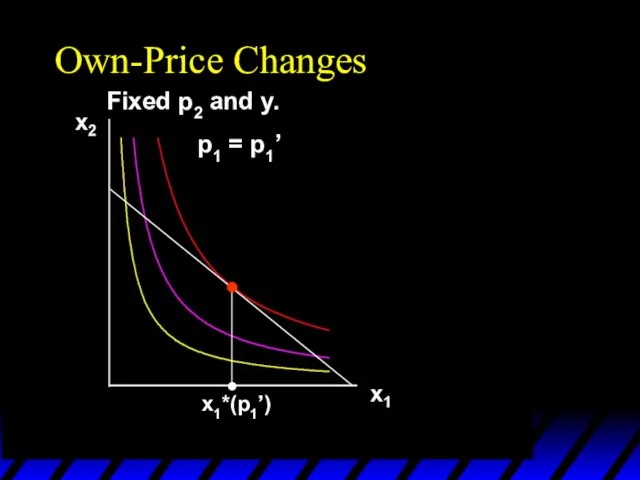
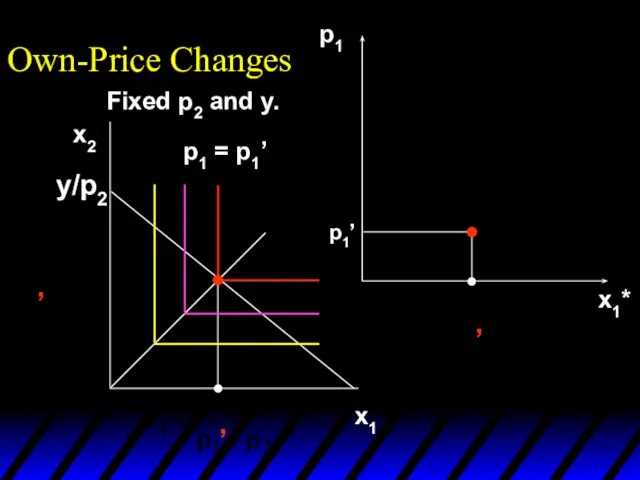
- 4. x1 x2 p1 = p1’ Fixed p2 and y. p1x1 + p2x2 = y Own-Price Changes
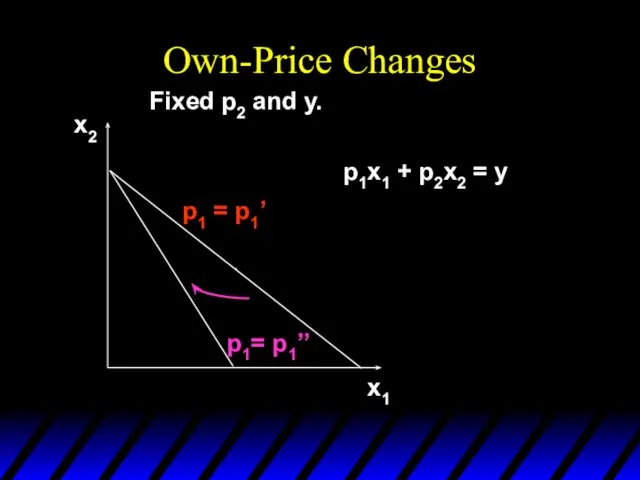
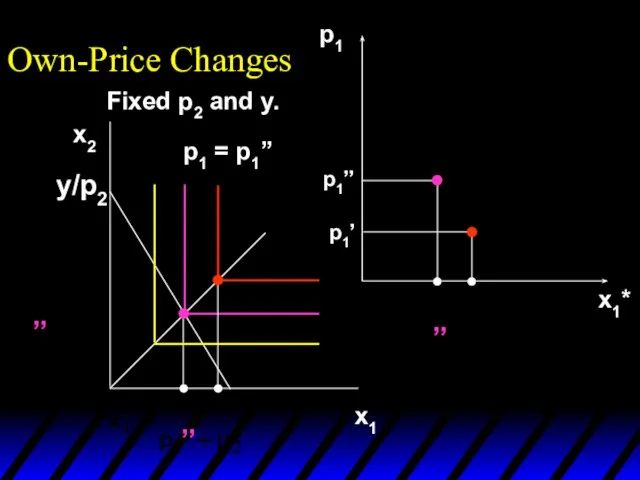
- 5. Own-Price Changes x1 x2 p1= p1’’ p1 = p1’ Fixed p2 and y. p1x1 + p2x2
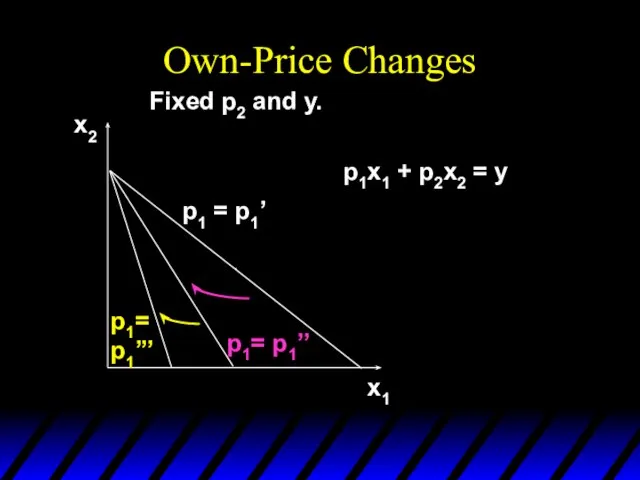
- 6. Own-Price Changes x1 x2 p1= p1’’ p1= p1’’’ Fixed p2 and y. p1 = p1’ p1x1
- 7. p1 = p1’ Own-Price Changes Fixed p2 and y.
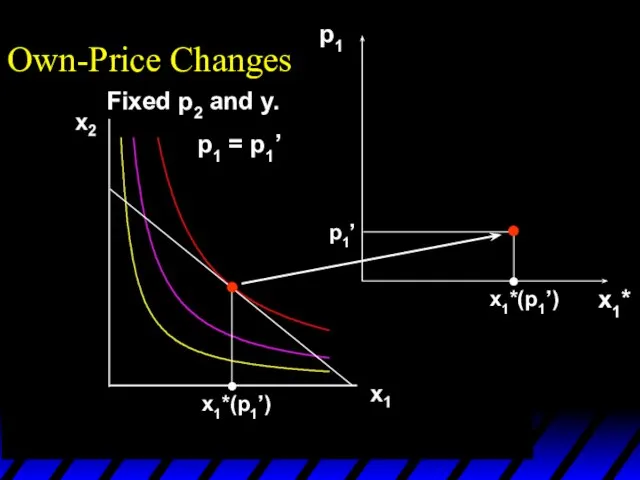
- 8. x1*(p1’) Own-Price Changes p1 = p1’ Fixed p2 and y.
- 9. x1*(p1’) p1 x1*(p1’) p1’ x1* Own-Price Changes Fixed p2 and y. p1 = p1’
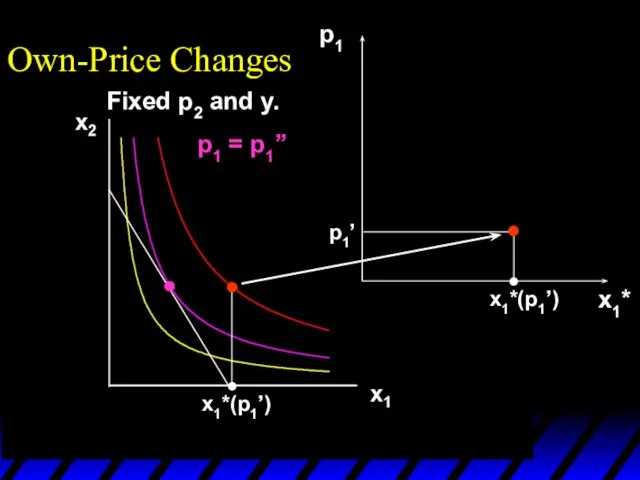
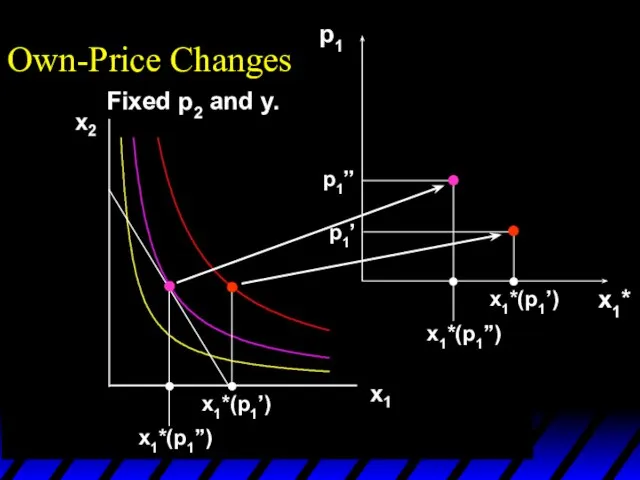
- 10. x1*(p1’) p1 x1*(p1’) p1’ p1 = p1’’ x1* Own-Price Changes Fixed p2 and y.
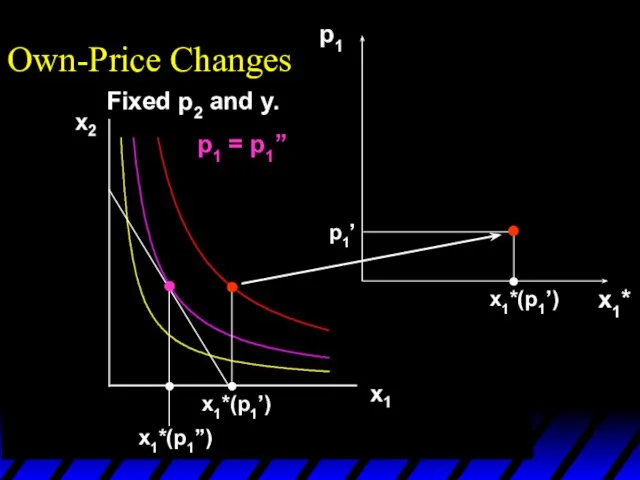
- 11. x1*(p1’) x1*(p1’’) p1 x1*(p1’) p1’ p1 = p1’’ x1* Own-Price Changes Fixed p2 and y.
- 12. x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’) p1’ p1’’ x1* Own-Price Changes Fixed p2 and y.
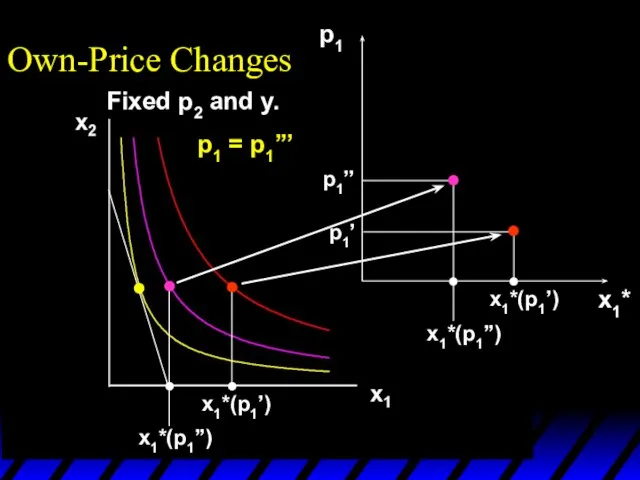
- 13. x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’) p1’ p1’’ p1 = p1’’’ x1* Own-Price Changes Fixed p2 and
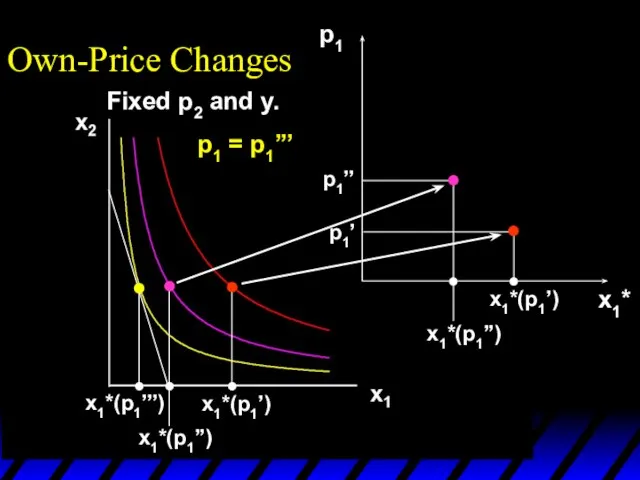
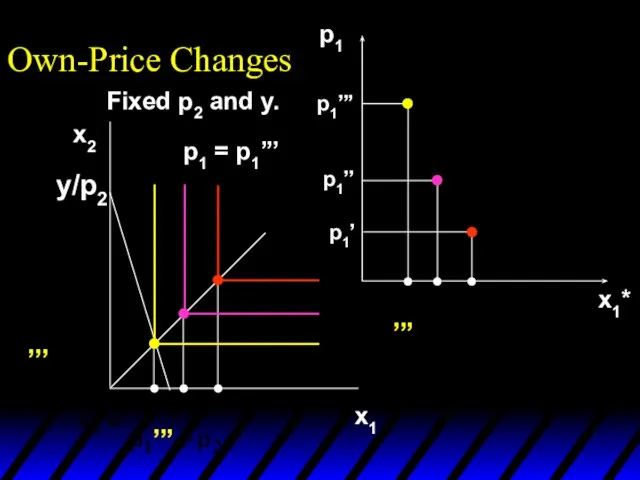
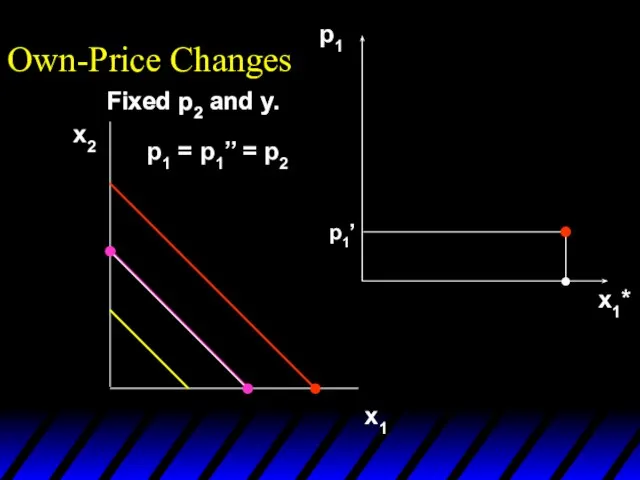
- 14. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’) p1’ p1’’ p1 = p1’’’ x1* Own-Price Changes Fixed p2
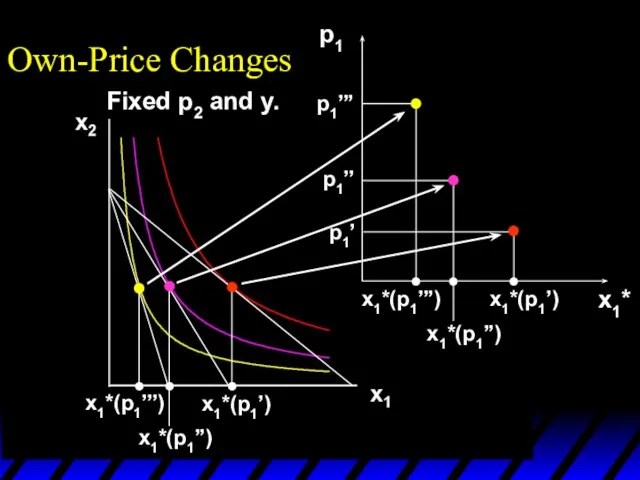
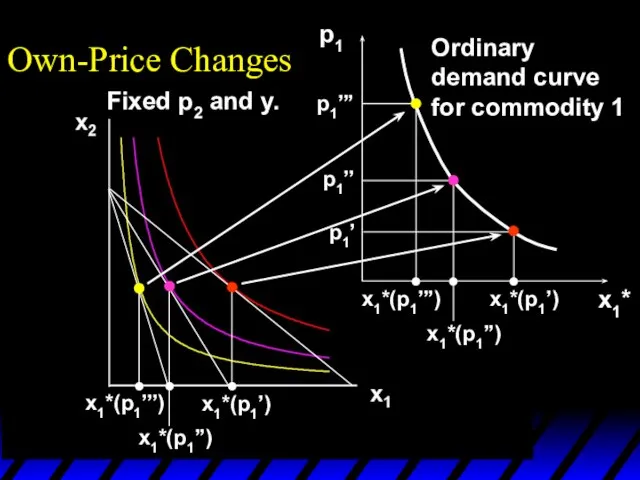
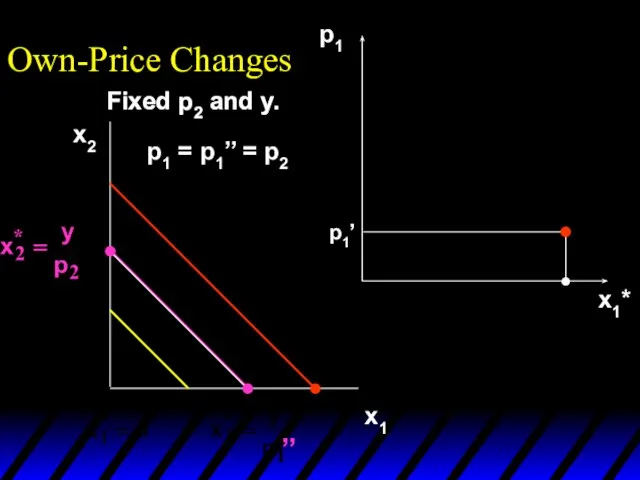
- 15. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’’) x1*(p1’’) p1’ p1’’ p1’’’ x1* Own-Price Changes Fixed p2 and
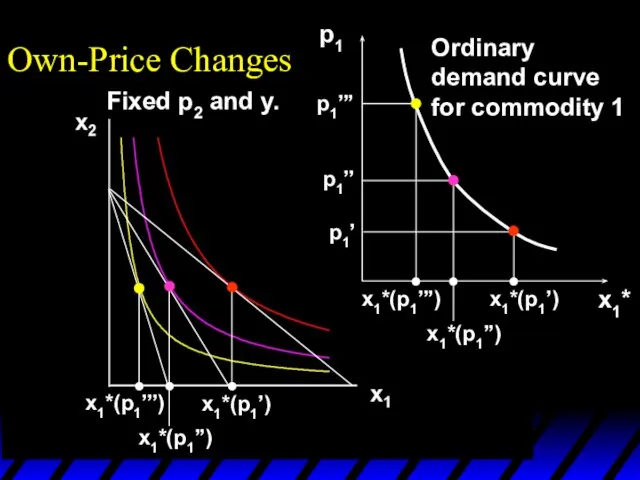
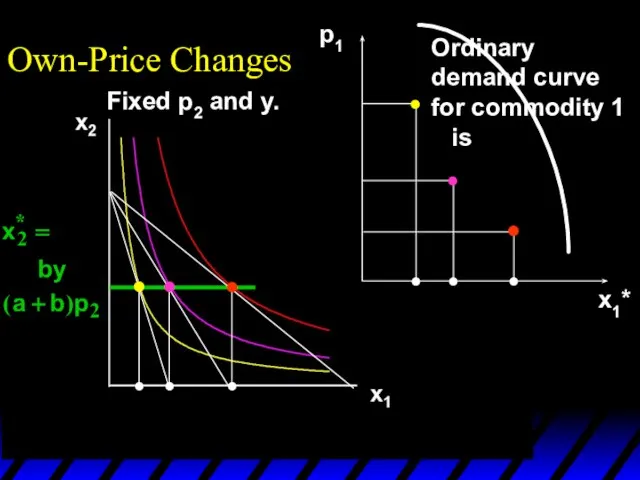
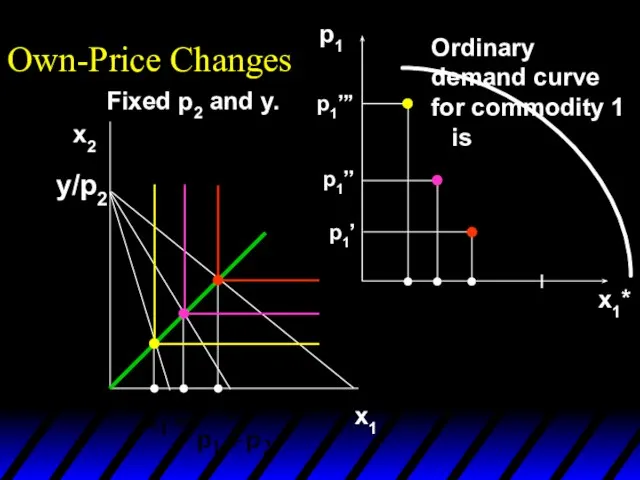
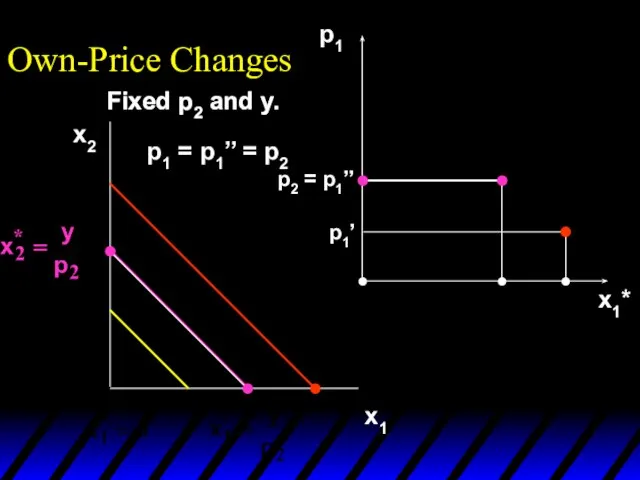
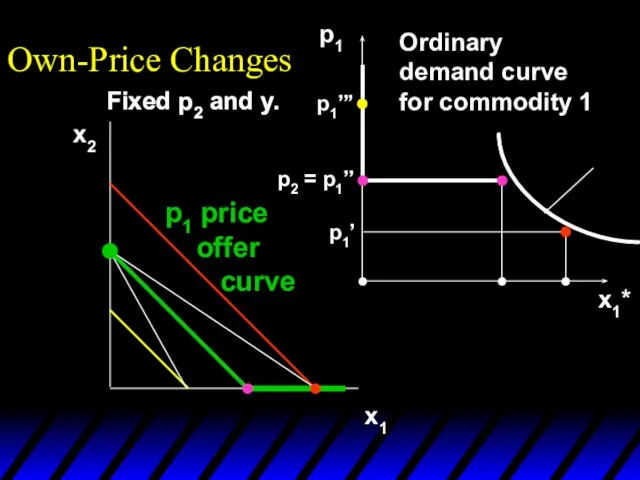
- 16. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’’) x1*(p1’’) p1’ p1’’ p1’’’ x1* Own-Price Changes Ordinary demand curve
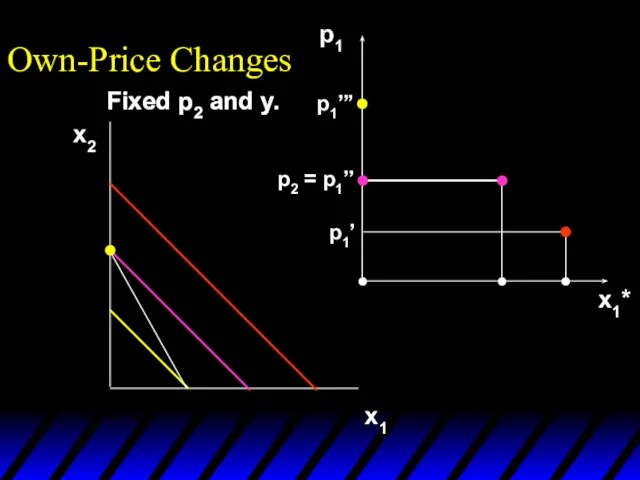
- 17. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’’) x1*(p1’’) p1’ p1’’ p1’’’ x1* Own-Price Changes Ordinary demand curve
- 18. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1*(p1’) x1*(p1’’’) x1*(p1’’) p1’ p1’’ p1’’’ x1* Own-Price Changes Ordinary demand curve
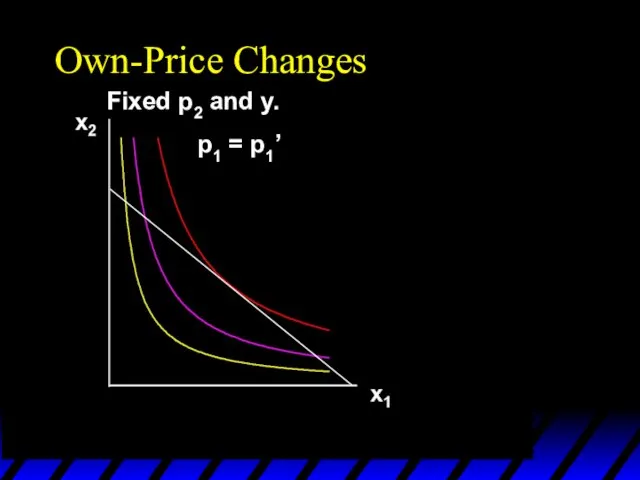
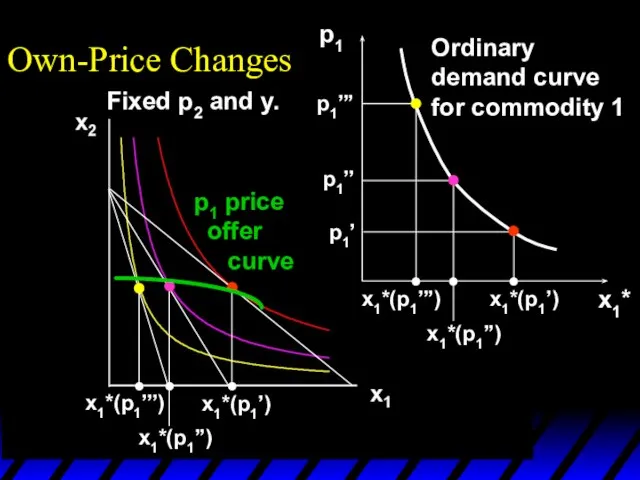
- 19. Own-Price Changes The curve containing all the utility-maximizing bundles traced out as p1 changes, with p2
- 20. Own-Price Changes What does a p1 price-offer curve look like for Cobb-Douglas preferences?
- 21. Own-Price Changes What does a p1 price-offer curve look like for Cobb-Douglas preferences? Take Then the
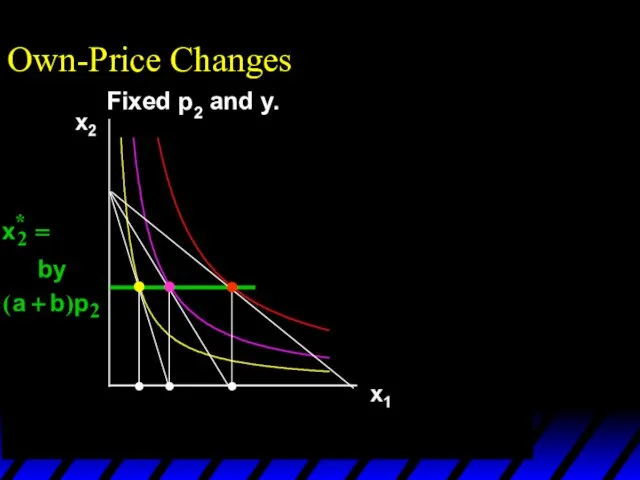
- 22. Own-Price Changes and Notice that x2* does not vary with p1 so the p1 price offer
- 23. Own-Price Changes and Notice that x2* does not vary with p1 so the p1 price offer
- 24. Own-Price Changes and Notice that x2* does not vary with p1 so the p1 price offer
- 25. Own-Price Changes and Notice that x2* does not vary with p1 so the p1 price offer
- 26. x1*(p1’’’) x1*(p1’) x1*(p1’’) Own-Price Changes Fixed p2 and y.
- 27. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1 x1* Own-Price Changes Ordinary demand curve for commodity 1 is Fixed p2
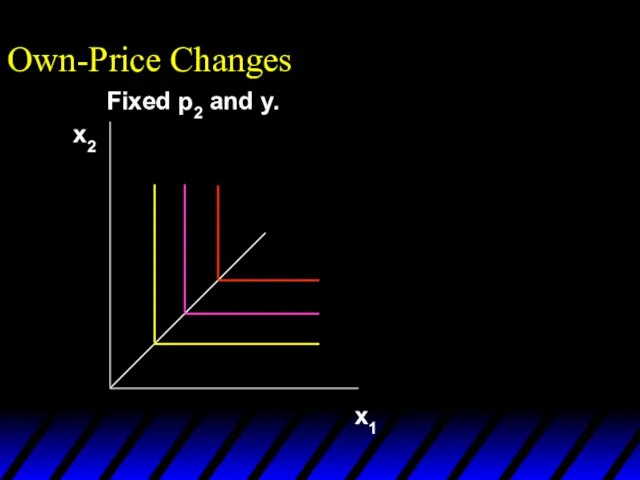
- 28. Own-Price Changes What does a p1 price-offer curve look like for a perfect-complements utility function?
- 29. Own-Price Changes What does a p1 price-offer curve look like for a perfect-complements utility function? Then
- 30. Own-Price Changes
- 31. Own-Price Changes With p2 and y fixed, higher p1 causes smaller x1* and x2*.
- 32. Own-Price Changes With p2 and y fixed, higher p1 causes smaller x1* and x2*. As
- 33. Own-Price Changes With p2 and y fixed, higher p1 causes smaller x1* and x2*. As As
- 34. Fixed p2 and y. Own-Price Changes x1 x2
- 35. p1 x1* Fixed p2 and y. Own-Price Changes x1 x2 p1’ ’ p1 = p1’ ’
- 36. p1 x1* Fixed p2 and y. Own-Price Changes x1 x2 p1’ p1’’ p1 = p1’’ ’’
- 37. p1 x1* Fixed p2 and y. Own-Price Changes x1 x2 p1’ p1’’ p1’’’ p1 = p1’’’
- 38. p1 x1* Ordinary demand curve for commodity 1 is Fixed p2 and y. Own-Price Changes x1
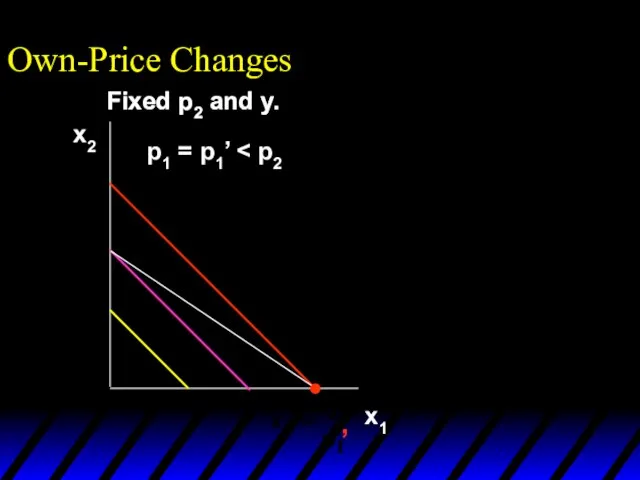
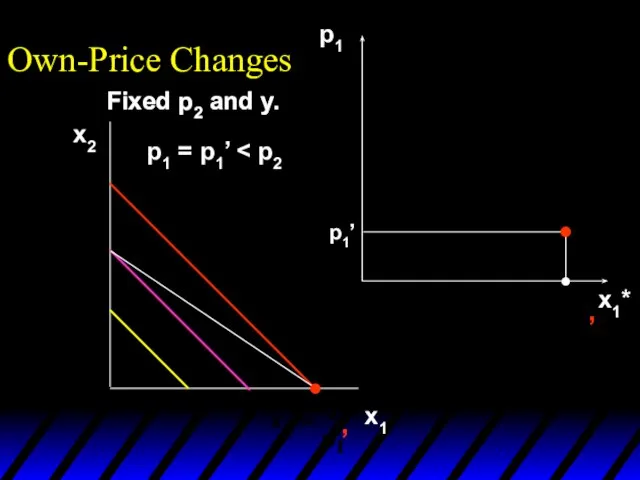
- 39. Own-Price Changes What does a p1 price-offer curve look like for a perfect-substitutes utility function? Then
- 40. Own-Price Changes and
- 41. Fixed p2 and y. Own-Price Changes x2 x1 Fixed p2 and y. p1 = p1’ ’
- 42. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1
- 43. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1
- 44. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1
- 45. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1
- 46. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1
- 47. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p1’’’
- 48. Fixed p2 and y. Own-Price Changes x2 x1 p1 x1* Fixed p2 and y. p1’ p2
- 49. Own-Price Changes Usually we ask “Given the price for commodity 1 what is the quantity demanded
- 50. Own-Price Changes p1 x1* p1’ Given p1’, what quantity is demanded of commodity 1?
- 51. Own-Price Changes p1 x1* p1’ Given p1’, what quantity is demanded of commodity 1? Answer: x1’
- 52. Own-Price Changes p1 x1* x1’ Given p1’, what quantity is demanded of commodity 1? Answer: x1’
- 53. Own-Price Changes p1 x1* p1’ x1’ Given p1’, what quantity is demanded of commodity 1? Answer:
- 54. Own-Price Changes Taking quantity demanded as given and then asking what must be price describes the
- 55. Own-Price Changes Inverse demand function At optimal choice |MRS| = p1/p2 Therefore: p1 = p2 |MRS|
- 56. Own-Price Changes Inverse demand function If good 2 is money, then MRS (and inverse demand function)
- 57. Own-Price Changes A Cobb-Douglas example: is the ordinary demand function and is the inverse demand function.
- 58. Own-Price Changes A perfect-complements example: is the ordinary demand function and is the inverse demand function.
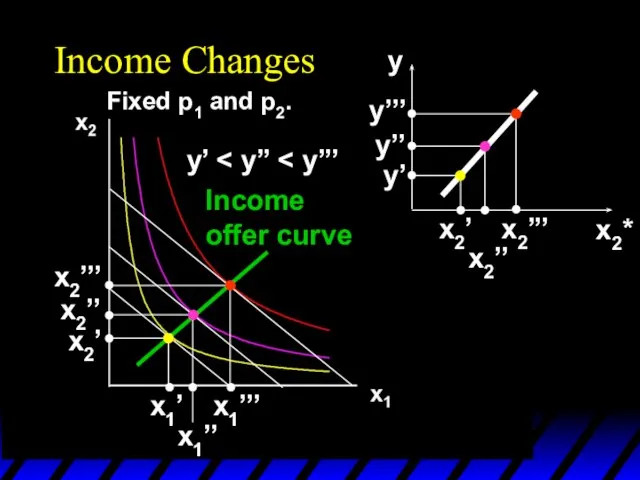
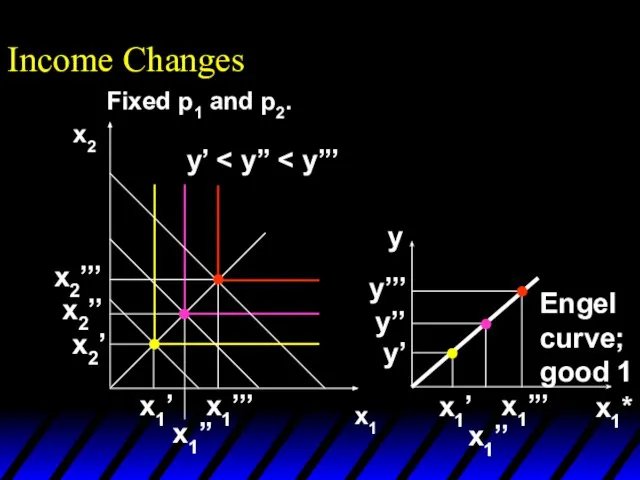
- 59. Income Changes How does the value of x1*(p1,p2,y) change as y changes, holding both p1 and
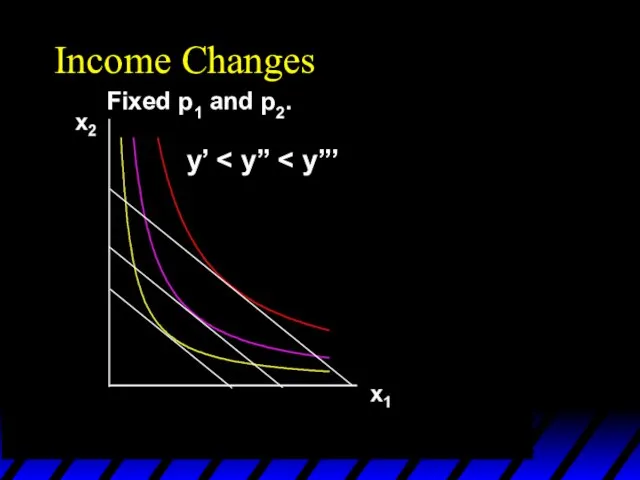
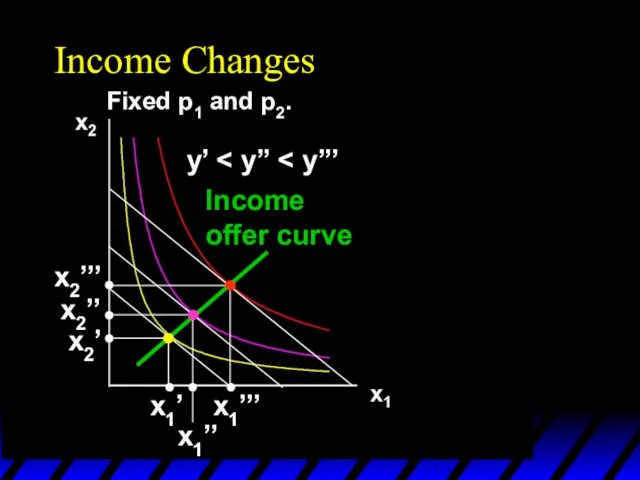
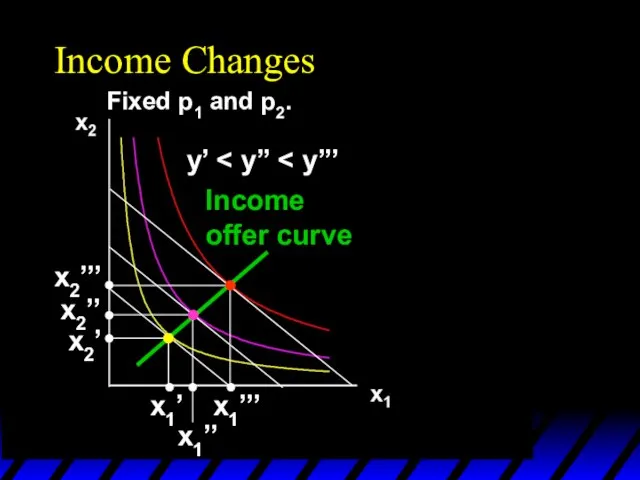
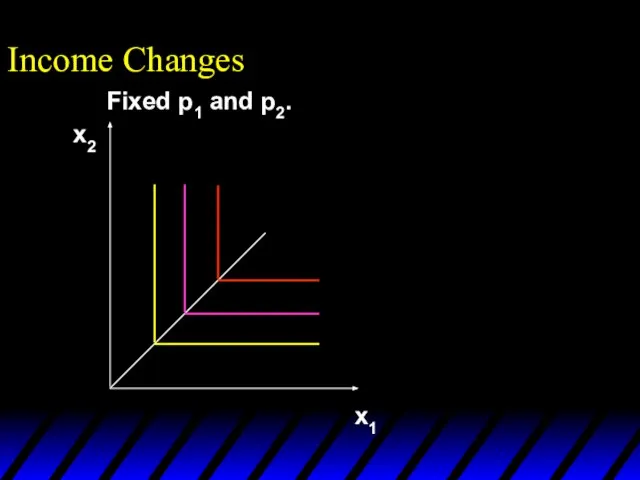
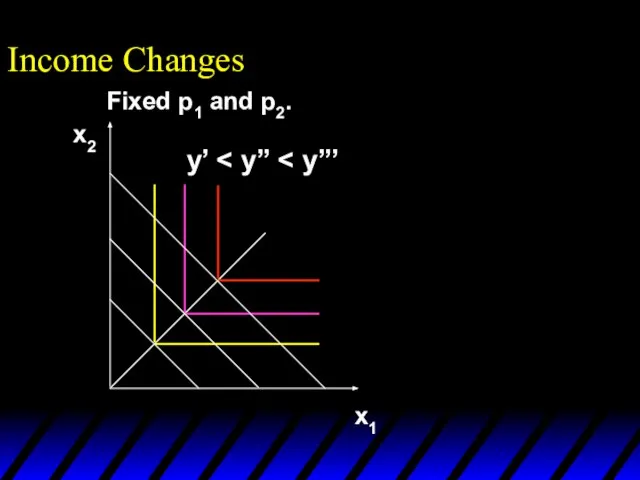
- 60. Income Changes Fixed p1 and p2. y’
- 61. Income Changes Fixed p1 and p2. y’
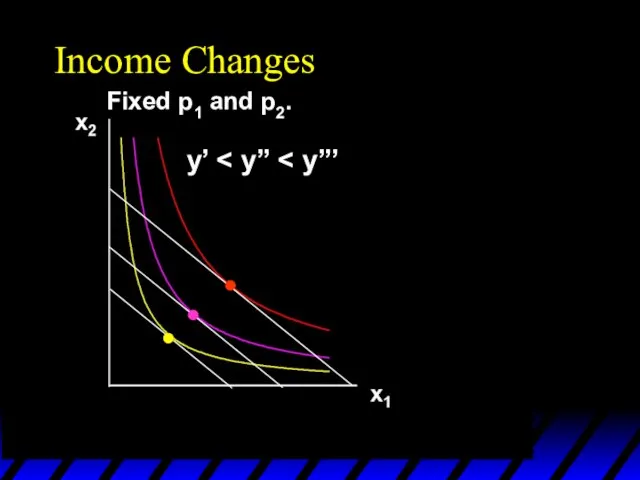
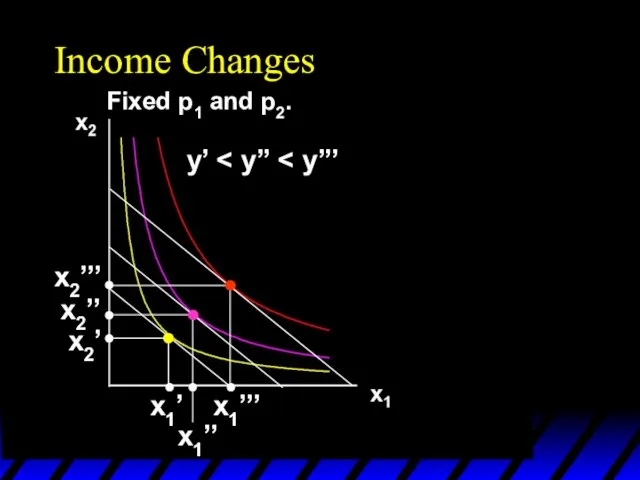
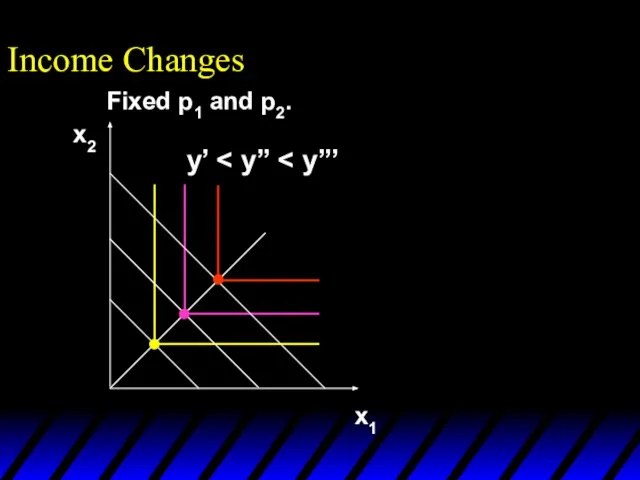
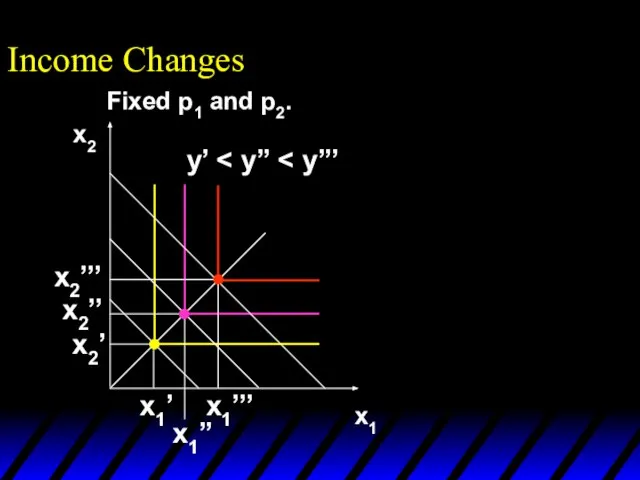
- 62. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’
- 63. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
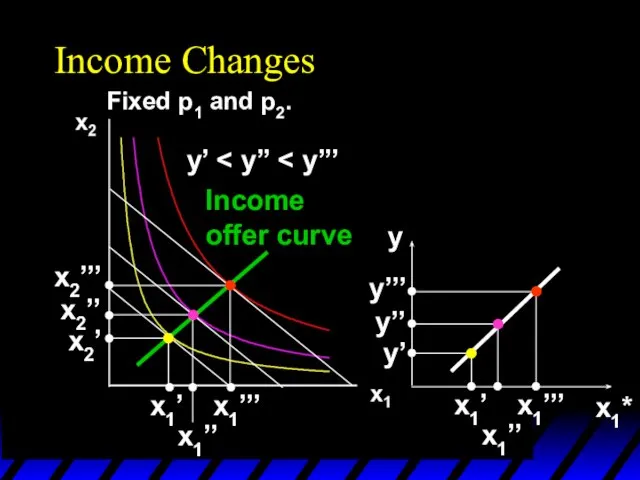
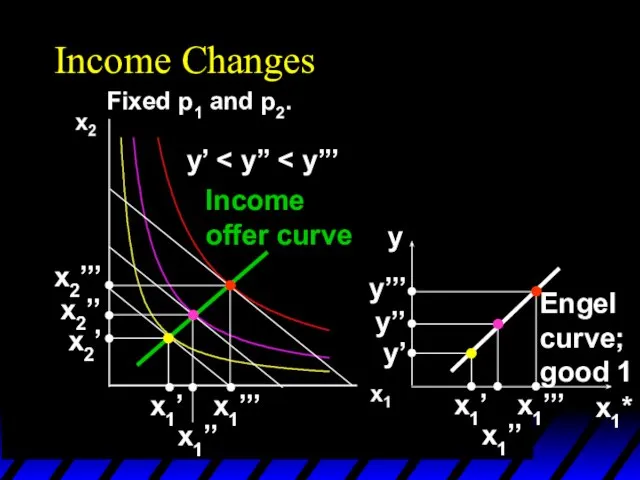
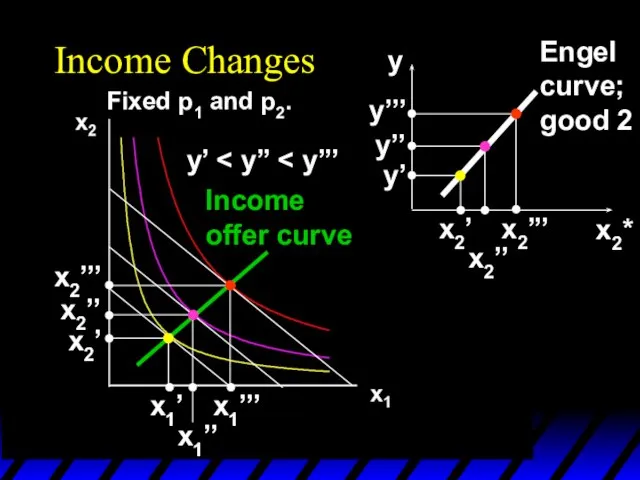
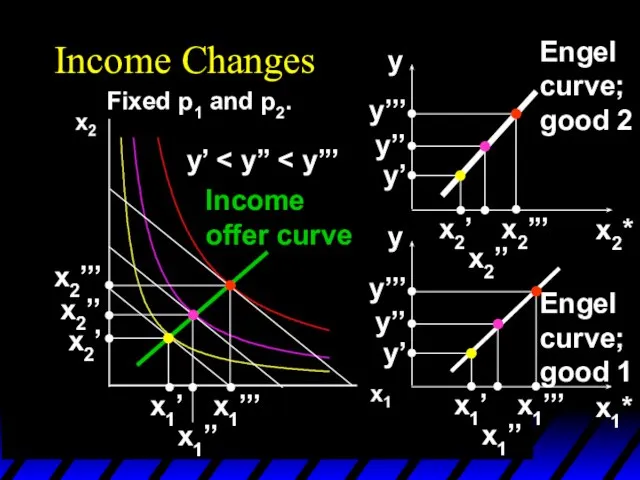
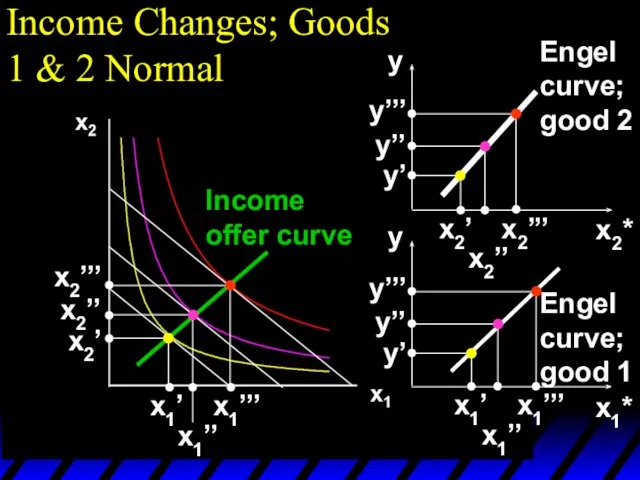
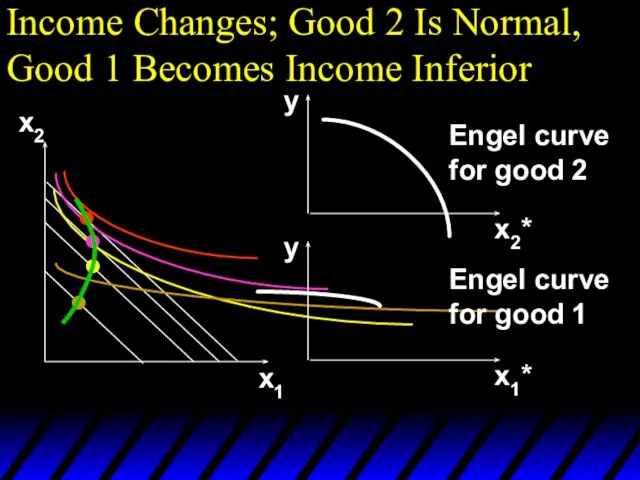
- 64. Income Changes A plot of quantity demanded against income is called an Engel curve.
- 65. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
- 66. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
- 67. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
- 68. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
- 69. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
- 70. Income Changes Fixed p1 and p2. y’ x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
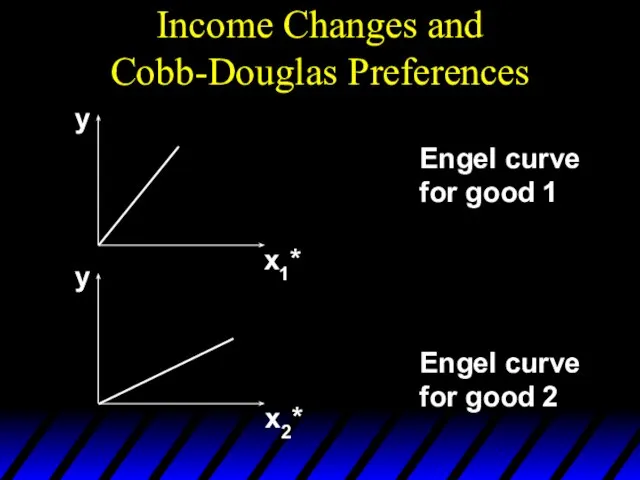
- 71. Income Changes and Cobb-Douglas Preferences An example of computing the equations of Engel curves; the Cobb-Douglas
- 72. Income Changes and Cobb-Douglas Preferences Rearranged to isolate y, these are: Engel curve for good 1
- 73. Income Changes and Cobb-Douglas Preferences y y x1* x2* Engel curve for good 1 Engel curve
- 74. Income Changes and Perfectly-Complementary Preferences Another example of computing the equations of Engel curves; the perfectly-complementary
- 75. Income Changes and Perfectly-Complementary Preferences Rearranged to isolate y, these are: Engel curve for good 1
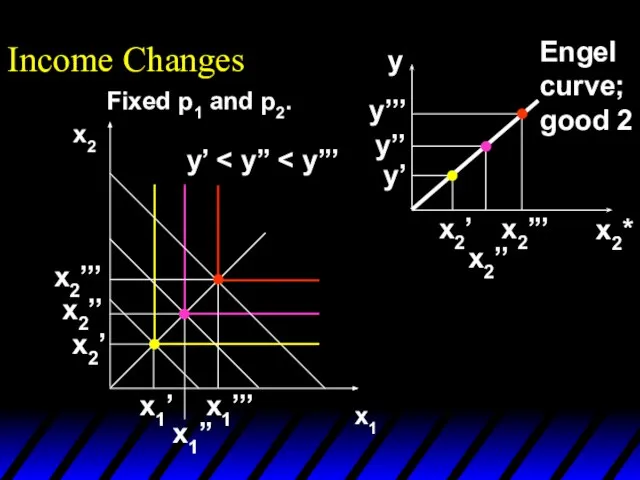
- 76. Fixed p1 and p2. Income Changes x1 x2
- 77. Income Changes x1 x2 y’ Fixed p1 and p2.
- 78. Income Changes x1 x2 y’ Fixed p1 and p2.
- 79. Income Changes x1 x2 y’ x1’’ x1’ x2’’’ x2’’ x2’ x1’’’ Fixed p1 and p2.
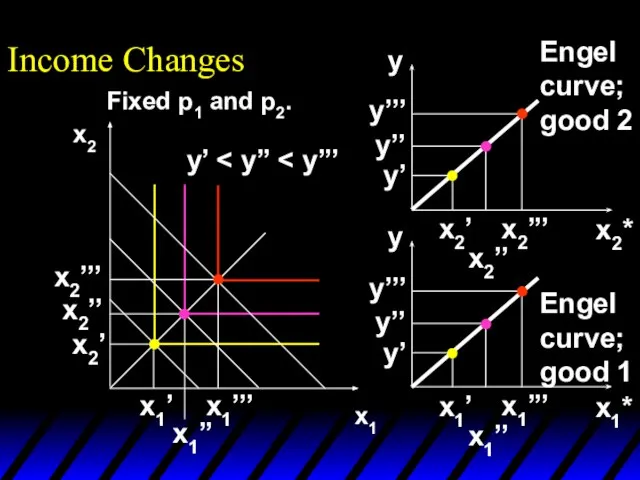
- 80. Income Changes x1 x2 y’ x1’’ x1’ x2’’’ x2’’ x2’ x1’’’ x1* y y’ y’’ y’’’
- 81. Income Changes x1 x2 y’ x1’’ x1’ x2’’’ x2’’ x2’ x1’’’ x2* y x2’’’ x2’’ x2’
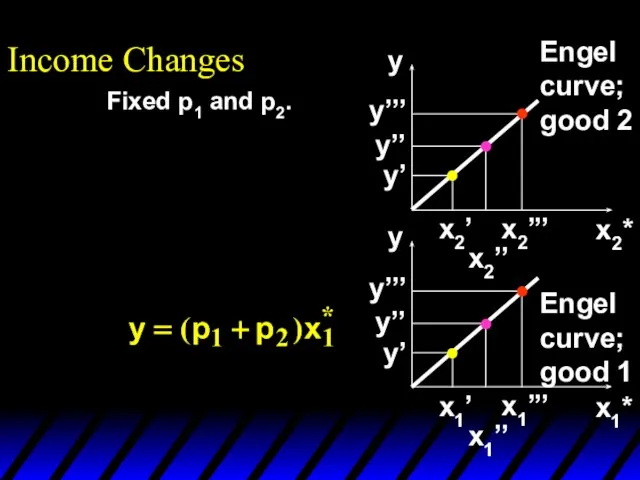
- 82. Income Changes x1 x2 y’ x1’’ x1’ x2’’’ x2’’ x2’ x1’’’ x1* x2* y y x2’’’
- 83. Income Changes x1* x2* y y x2’’’ x2’’ x2’ y’ y’’ y’’’ y’ y’’ y’’’ x1’’’
- 84. Income Changes and Perfectly-Substitutable Preferences Another example of computing the equations of Engel curves; the perfectly-substitution
- 85. Income Changes and Perfectly-Substitutable Preferences
- 86. Income Changes and Perfectly-Substitutable Preferences Suppose p1
- 87. Income Changes and Perfectly-Substitutable Preferences Suppose p1 and
- 88. Income Changes and Perfectly-Substitutable Preferences Suppose p1 and and
- 89. Income Changes and Perfectly-Substitutable Preferences y y x1* x2* 0 Engel curve for good 1 Engel
- 90. Income Changes In every example so far the Engel curves have all been straight lines? Q:
- 91. Homotheticity A consumer’s preferences are homothetic if and only if for every k > 0. That
- 92. Income Effects -- A Nonhomothetic Example Quasilinear preferences are not homothetic. For example,
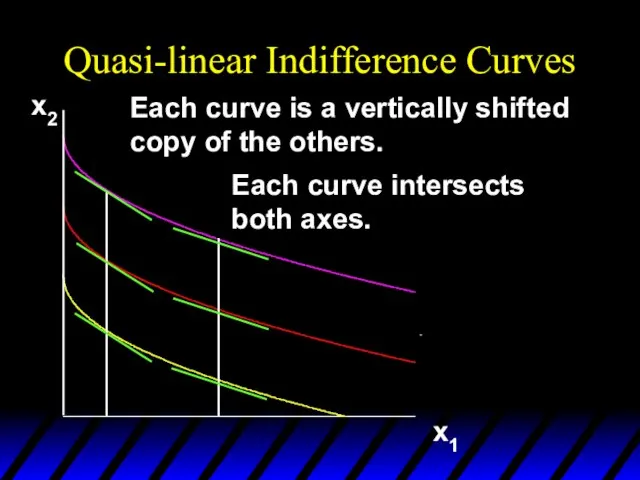
- 93. Quasi-linear Indifference Curves x2 x1 Each curve is a vertically shifted copy of the others. Each
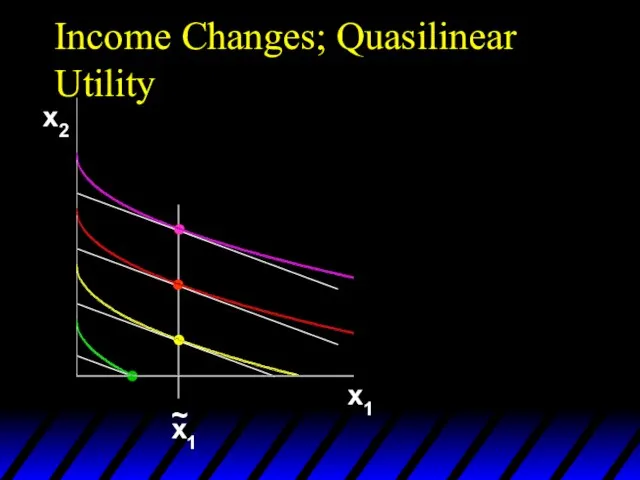
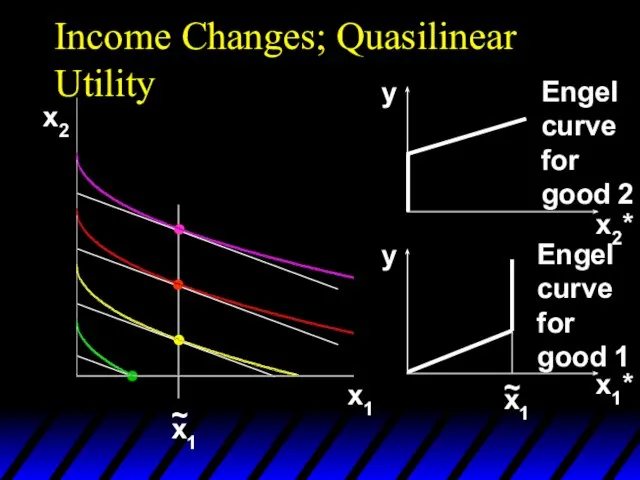
- 94. Income Changes; Quasilinear Utility x2 x1
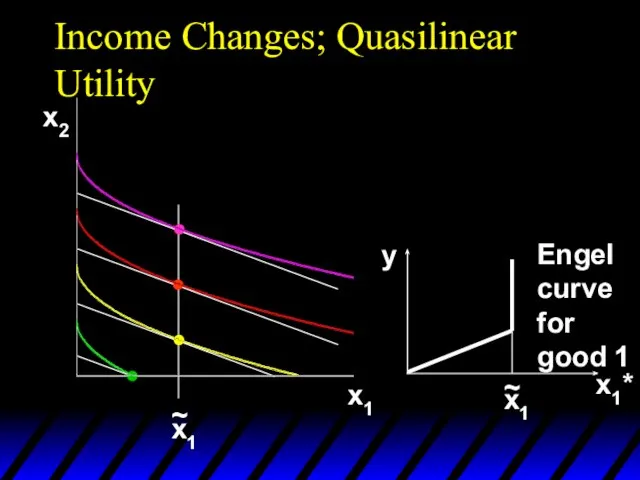
- 95. Income Changes; Quasilinear Utility x2 x1 x1* y x1 ~ Engel curve for good 1
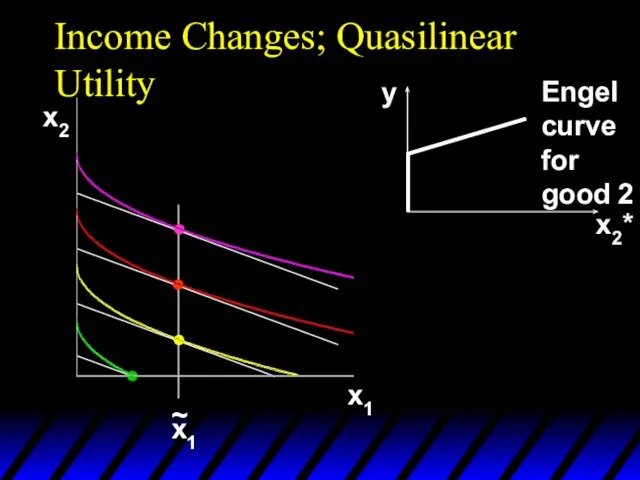
- 96. Income Changes; Quasilinear Utility x2 x1 x2* y Engel curve for good 2
- 97. Income Changes; Quasilinear Utility x2 x1 x1* x2* y y x1 ~ Engel curve for good
- 98. Income Effects A good for which quantity demanded rises with income is called normal. Therefore a
- 99. Income Effects A good for which quantity demanded falls as income increases is called income inferior.
- 100. Income Effects In the US over last hundred years income increased many times whereas the number
- 101. Income Changes; Goods 1 & 2 Normal x1’’’ x1’’ x1’ x2’’’ x2’’ x2’ Income offer curve
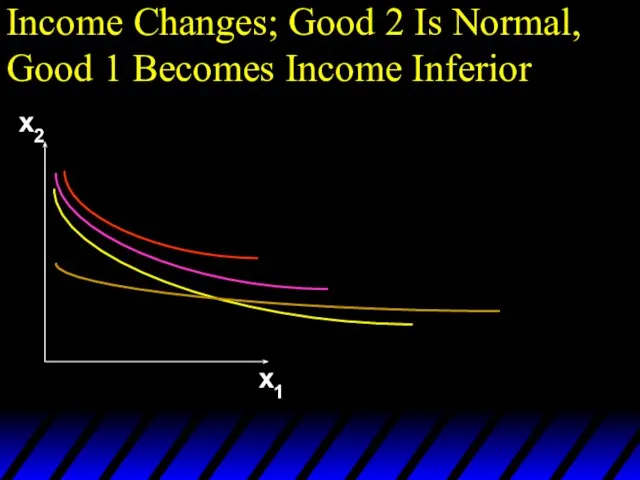
- 102. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1
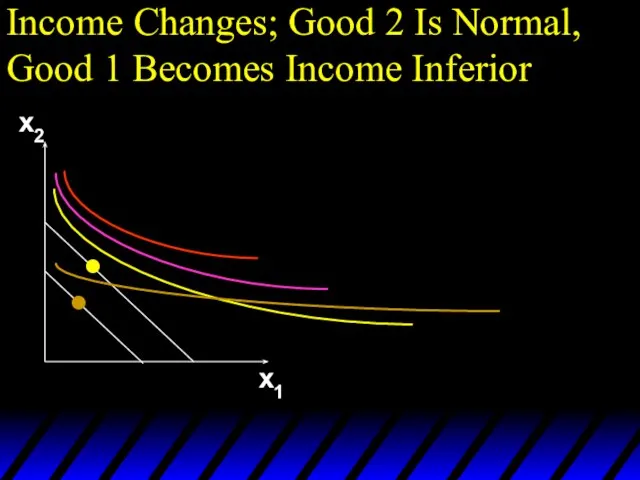
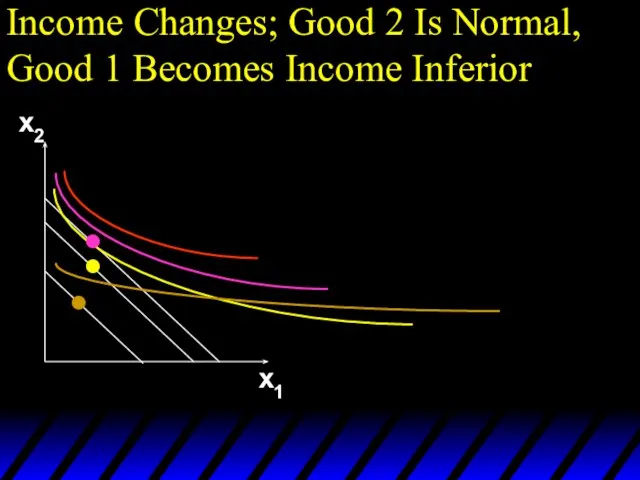
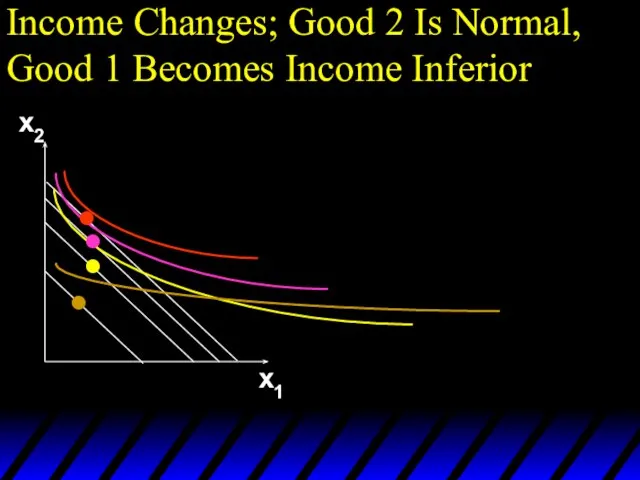
- 103. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1
- 104. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1
- 105. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1
- 106. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1
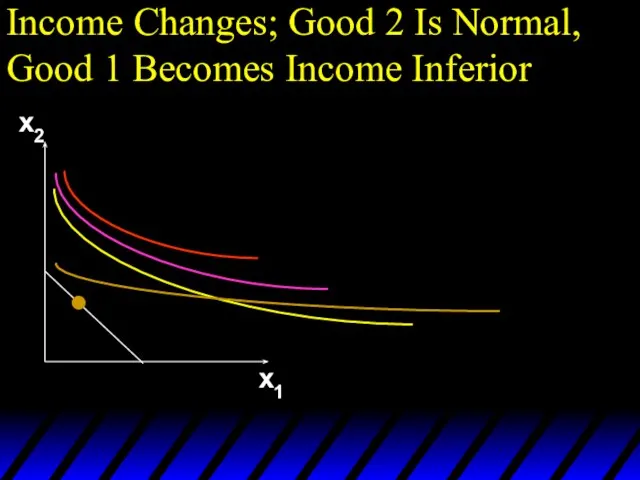
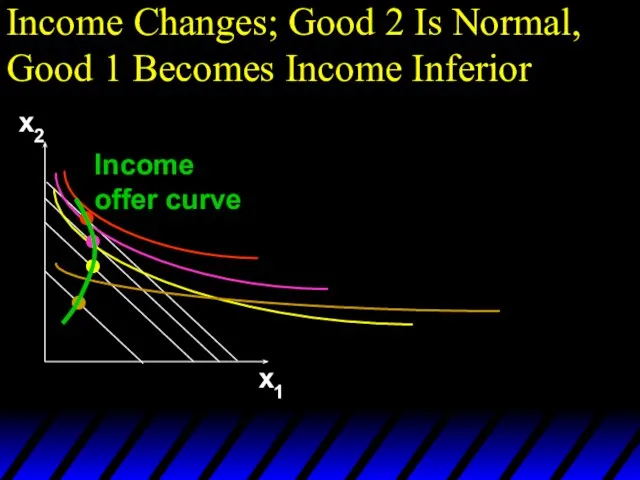
- 107. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1 Income offer curve
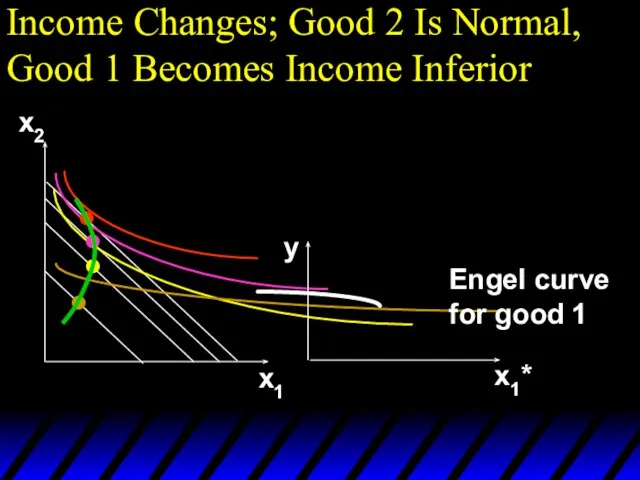
- 108. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1 x1* y Engel
- 109. Income Changes; Good 2 Is Normal, Good 1 Becomes Income Inferior x2 x1 x1* x2* y
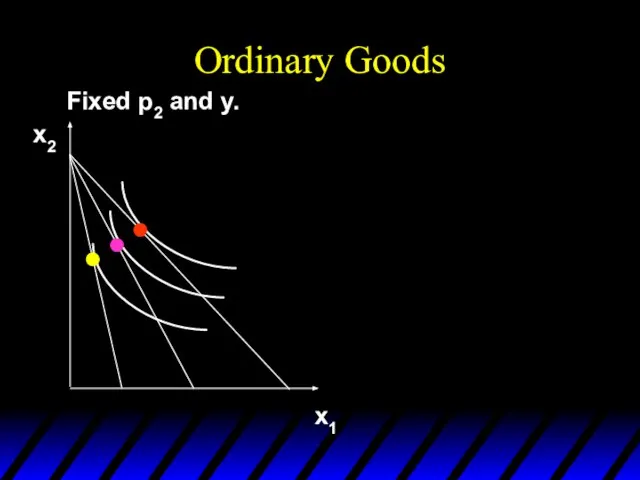
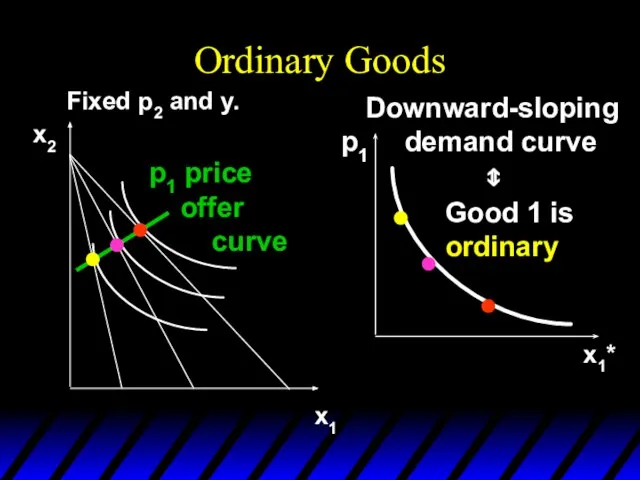
- 110. Ordinary Goods A good is called ordinary if the quantity demanded of it always increases as
- 111. Ordinary Goods Fixed p2 and y. x1 x2
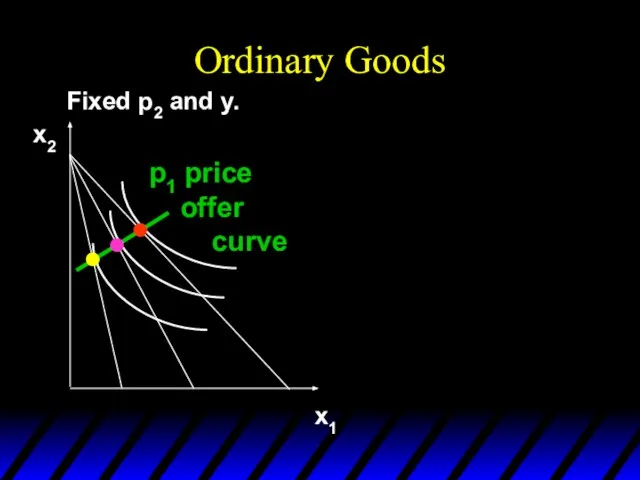
- 112. Ordinary Goods Fixed p2 and y. x1 x2 p1 price offer curve
- 113. Ordinary Goods Fixed p2 and y. x1 x2 p1 price offer curve x1* Downward-sloping demand curve
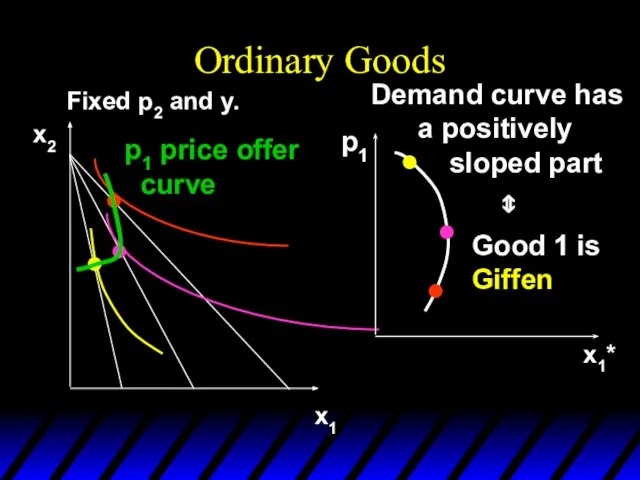
- 114. Giffen Goods If, for some values of its own price, the quantity demanded of a good
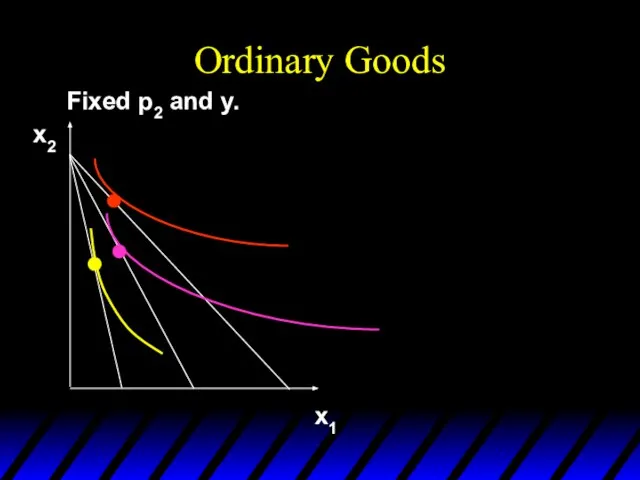
- 115. Ordinary Goods Fixed p2 and y. x1 x2
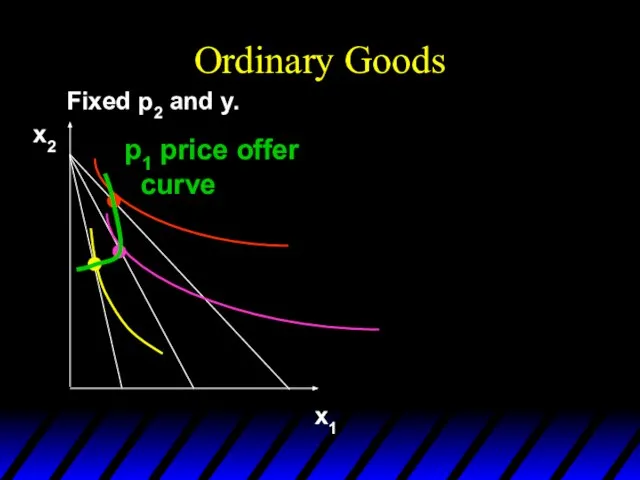
- 116. Ordinary Goods Fixed p2 and y. x1 x2 p1 price offer curve
- 117. Ordinary Goods Fixed p2 and y. x1 x2 p1 price offer curve x1* Demand curve has
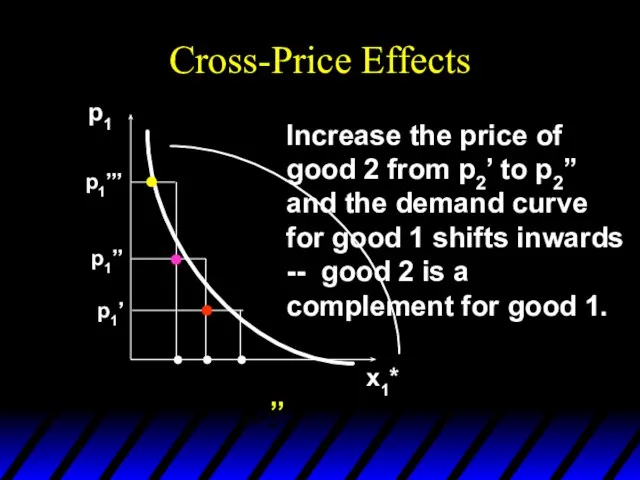
- 118. Cross-Price Effects If an increase in p2 increases demand for commodity 1 then commodity 1 is
- 119. Cross-Price Effects A perfect-complements example: so Therefore commodity 2 is a gross complement for commodity 1.
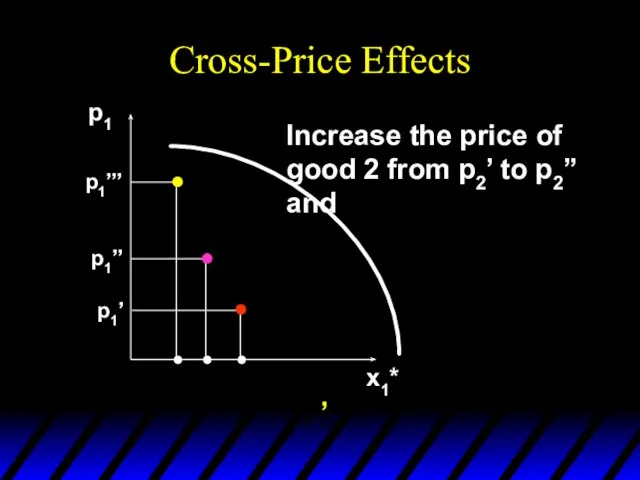
- 120. Cross-Price Effects p1 x1* p1’ p1’’ p1’’’ Increase the price of good 2 from p2’ to
- 121. Cross-Price Effects p1 x1* p1’ p1’’ p1’’’ Increase the price of good 2 from p2’ to
- 122. Cross-Price Effects A Cobb- Douglas example: so
- 124. Скачать презентацию



















































 Климат и погода
Климат и погода Венера (9 класс)
Венера (9 класс) Презентация на тему Скелет человека
Презентация на тему Скелет человека Урок русского языка
Урок русского языка С днём учителя
С днём учителя Синтез искусств в архитектуре. Витраж
Синтез искусств в архитектуре. Витраж Олимпиадное движение:итоги, проблемы, перспективы
Олимпиадное движение:итоги, проблемы, перспективы Прокрастинация
Прокрастинация Условия успешной реализации государственного образовательного стандарта основного общего образования
Условия успешной реализации государственного образовательного стандарта основного общего образования Интегрированный урок по рассказу А. П. Платонова «Юшка»
Интегрированный урок по рассказу А. П. Платонова «Юшка» Классификация запасов, расчет промышленных запасов шахтного поля, потерь и извлечения
Классификация запасов, расчет промышленных запасов шахтного поля, потерь и извлечения байт знаний
байт знаний  Деяние. Главная мысль
Деяние. Главная мысль Древнеславянская культура
Древнеславянская культура Правительство Российской Федерации
Правительство Российской Федерации ЭТИКЕТза праздничным столом
ЭТИКЕТза праздничным столом Презентация на тему Тепловые двигатели и их применение
Презентация на тему Тепловые двигатели и их применение  Множественное число существительных
Множественное число существительных Индонезия
Индонезия Стиль, как способность товаров удовлетворять социальные и эстетические потребности
Стиль, как способность товаров удовлетворять социальные и эстетические потребности Открытый банк заданий по математике Задача №14
Открытый банк заданий по математике Задача №14 1
1 Внешние силы изменяющие рельеф
Внешние силы изменяющие рельеф Презентация к уроку _Месяц и год_ (2 класс)
Презентация к уроку _Месяц и год_ (2 класс) Путь в жизни и в литературе Б.Л. Пастернак (1890 – 1960)
Путь в жизни и в литературе Б.Л. Пастернак (1890 – 1960) Бутербродлар. Һәм аларның төрләре
Бутербродлар. Һәм аларның төрләре Годовое и перспективное финансовое планирование. Виды бюджетного планирования
Годовое и перспективное финансовое планирование. Виды бюджетного планирования Диалог с ребенком
Диалог с ребенком