Содержание
- 2. Surfaces.
- 3. Surfaces. Classification. Determinant. Outline.
- 4. Surfaces. Classification. Determinant. Outline. Fundamentals: Surface of geometric solid is multiple of boundary points of a
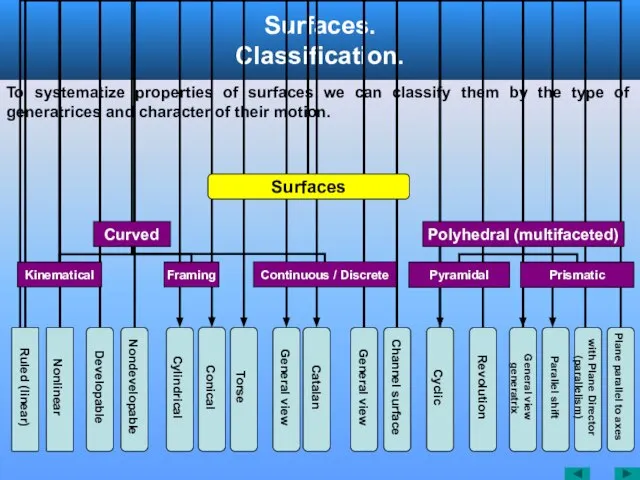
- 5. Surfaces. Classification. To systematize properties of surfaces we can classify them by the type of generatrices
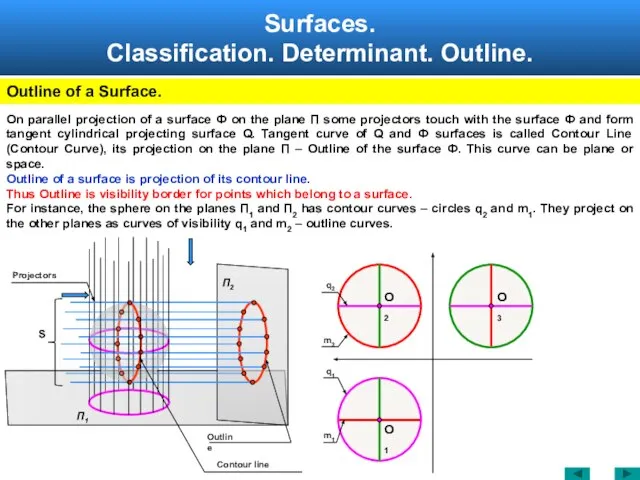
- 6. Surfaces. Classification. Determinant. Outline. Outline of a Surface. For a surface to be specified, it is
- 7. Surfaces. Classification. Determinant. Outline. Outline of a Surface. П2 S Contour line Outline Projectors O1 O2
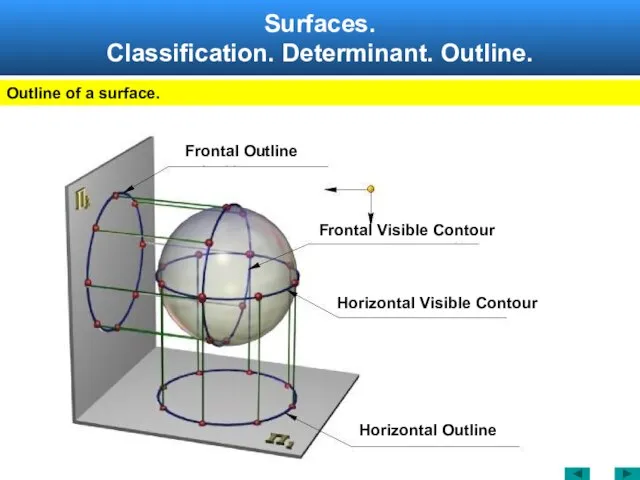
- 8. Surfaces. Classification. Determinant. Outline. Outline of a surface. Frontal Visible Contour Frontal Outline Horizontal Visible Contour
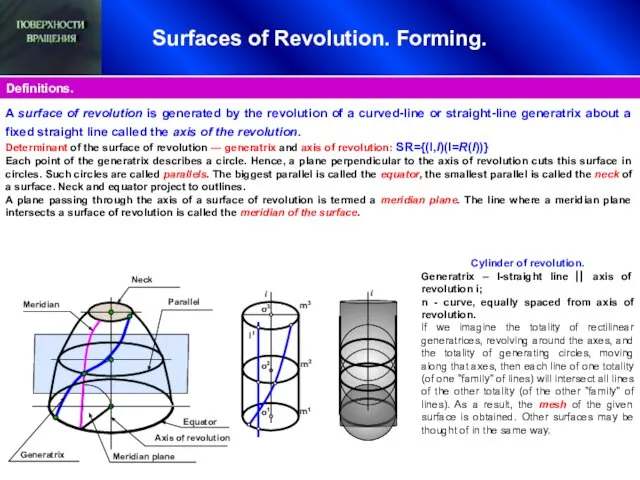
- 9. Surfaces of Revolution. Forming. Definitions. Parallel Meridian Generatrix Neck Axis of revolution l1 i m3 m2
- 10. Surfaces of Revolution. General.
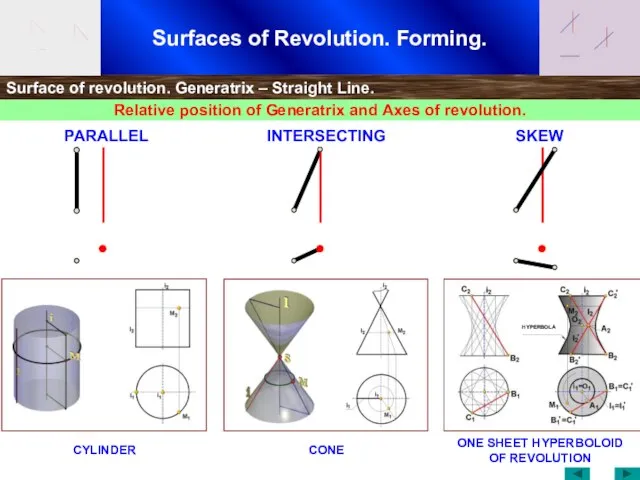
- 11. Surfaces of Revolution. Forming. Surface of revolution. Generatrix – Straight Line. Relative position of Generatrix and
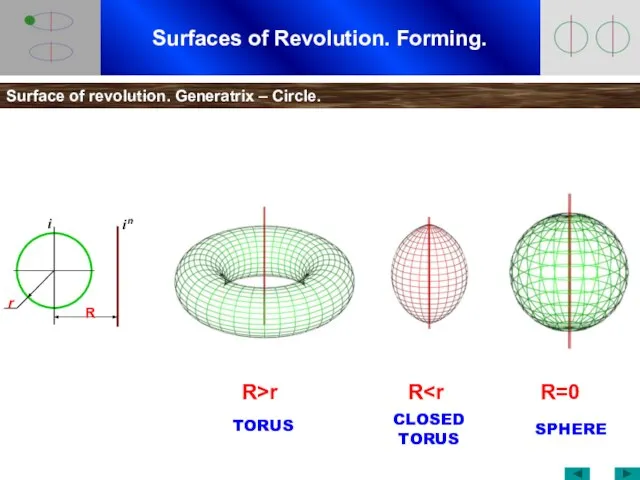
- 12. Surfaces of Revolution. Forming. Surface of revolution. Generatrix – Circle. R>r R R=0 TORUS CLOSED TORUS
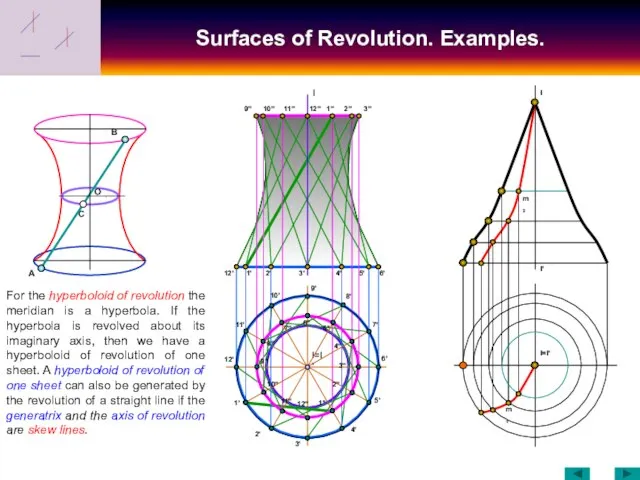
- 13. Surfaces of Revolution. Examples. 12' I I=I' 10'' 1' 2' 3' 4' 5' 6' 9'' 11''
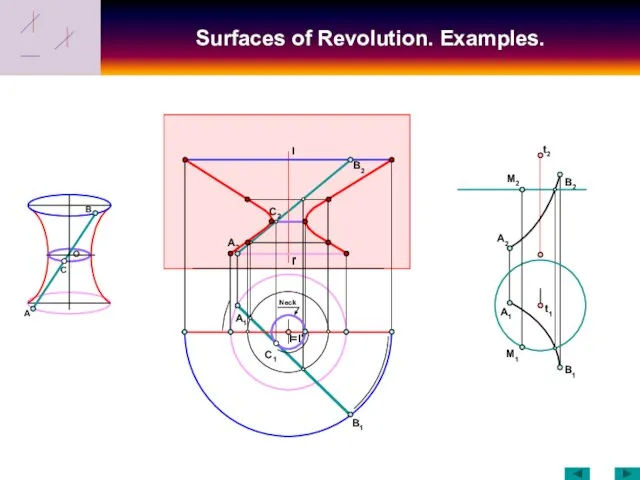
- 14. Surfaces of Revolution. Examples. C O B I I' A B1 B2 A2 A1 B1 A2
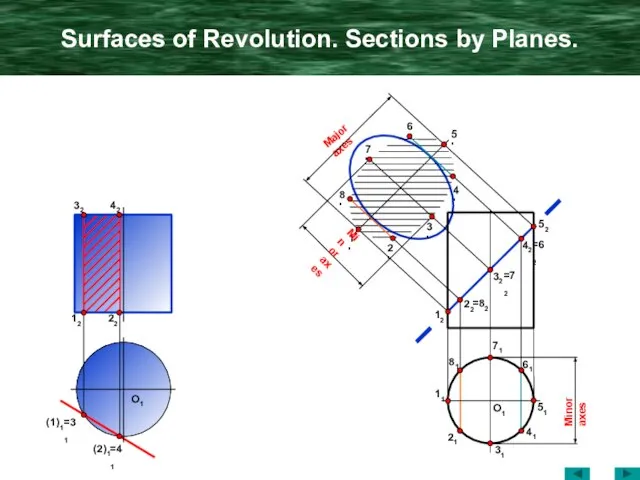
- 15. Surfaces of Revolution. Sections by Planes. O1 42 32 22 12 (1)1 =31 (2)1 =41 11
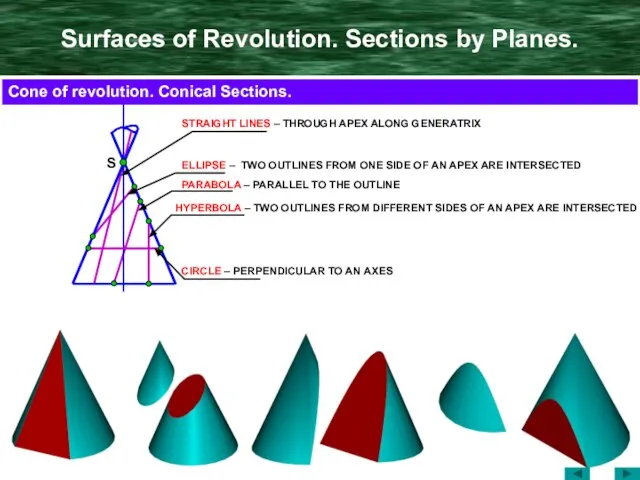
- 16. Surfaces of Revolution. Sections by Planes. S ELLIPSE – TWO OUTLINES FROM ONE SIDE OF AN
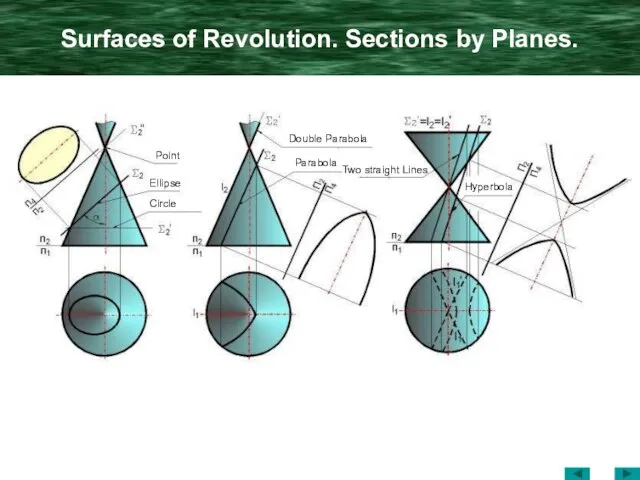
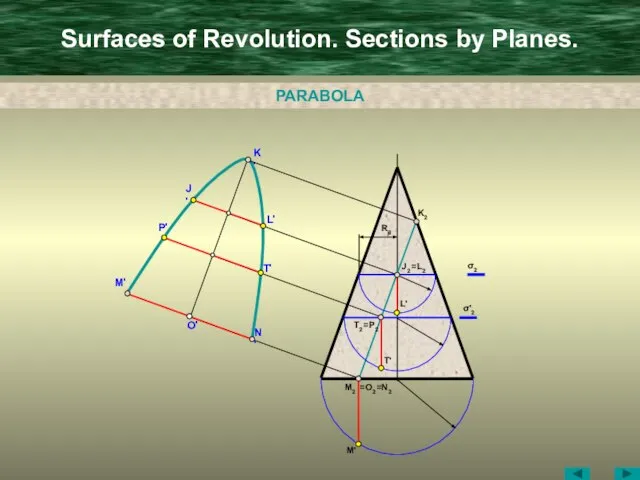
- 17. Surfaces of Revolution. Sections by Planes. Point Ellipse Circle Double Parabola Parabola Two straight Lines Hyperbola
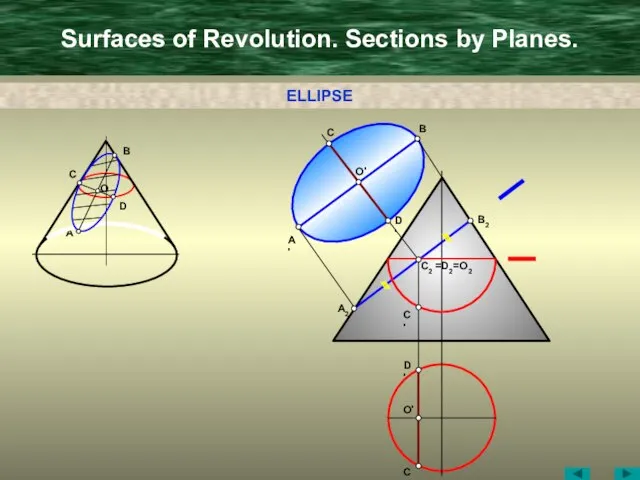
- 18. Surfaces of Revolution. Sections by Planes. A C B D D' B' C' O' A' B2
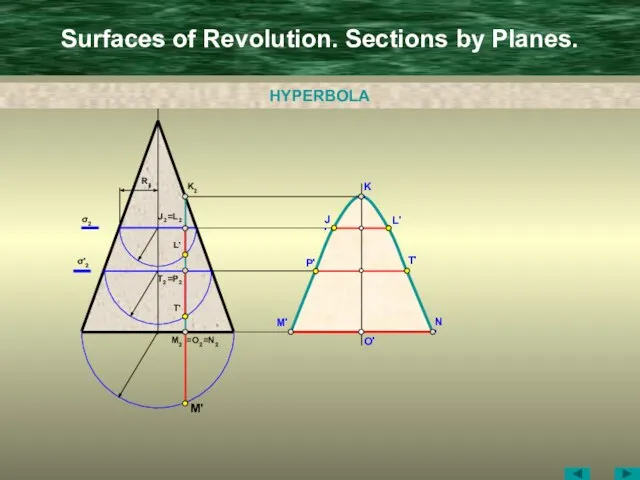
- 19. Surfaces of Revolution. Sections by Planes. O' M2 =N2 =O2 M' M' K2 J2 =L2 L'
- 20. Surfaces of Revolution. Sections by Planes. O' M2 =N2 =O2 M' M' K2 J2 =L2 L'
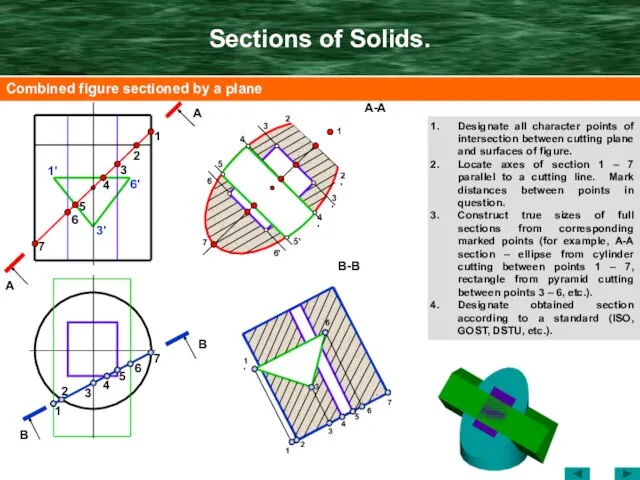
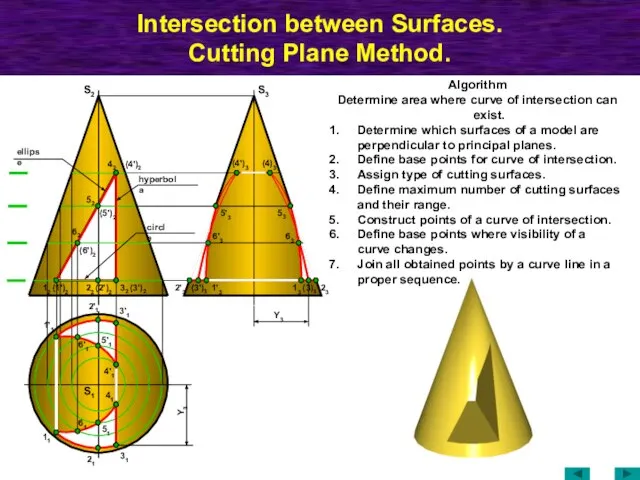
- 21. Sections of Solids. Designate all character points of intersection between cutting plane and surfaces of figure.
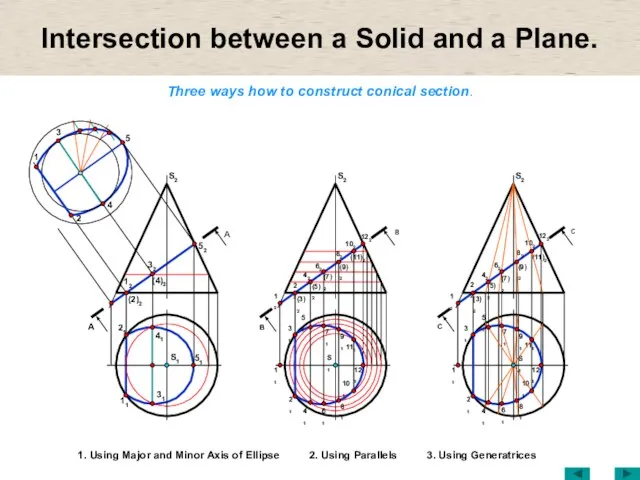
- 22. Intersection between a Solid and a Plane. Three ways how to construct conical section. 1. Using
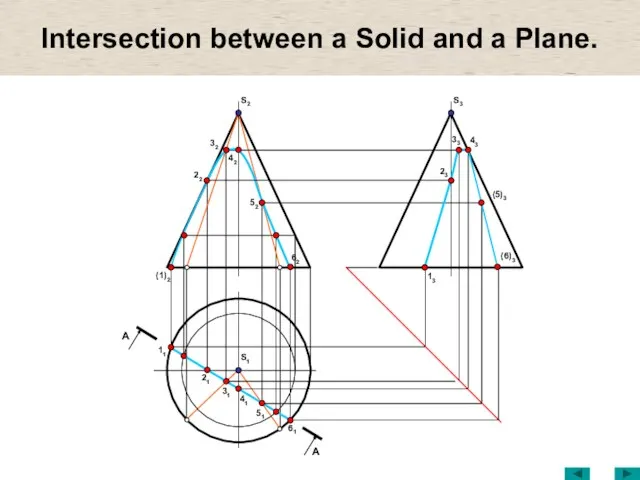
- 23. Intersection between a Solid and a Plane. S1 (1)2 32 22 52 31 42 S2 21
- 24. Surfaces. Ruled surfaces. A surface which can be generated by a straight line is called the
- 25. Surfaces. Developable Ruled surfaces. Some curved surfaces can be developed so that they coincide completely (with
- 26. Surfaces. Ruled surfaces with one Diretrix. Conical Surface m1 m2 A2 A S m M2 M1
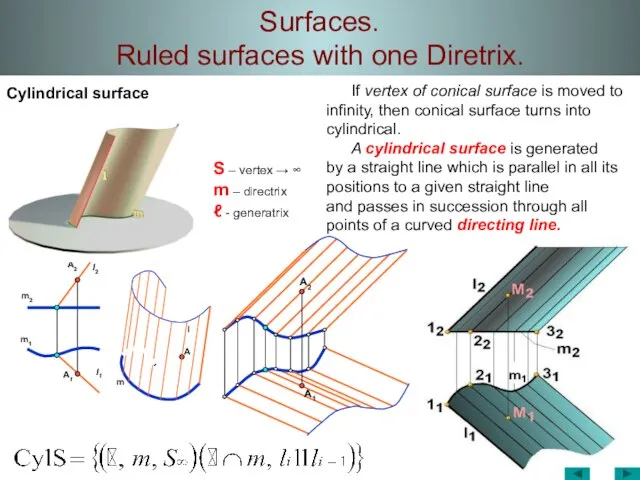
- 27. Surfaces. Ruled surfaces with one Diretrix. Cylindrical surface A2 m2 m1 A1 m l1 A l
- 28. Surfaces. Ruled surfaces with one Diretrix. n, k – border lines l1 m1 B1 m2 l2
- 29. Surfaces. Ruled surfaces with one Diretrix. Beveled Gear surface Spur Gear surface
- 30. Surfaces. Ruled surfaces with two Diretrices. where, l— generatrix, m, n —directrices; σ — plane director.
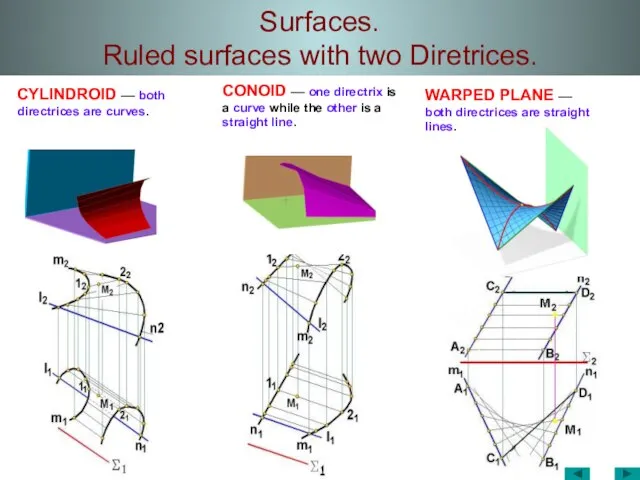
- 31. Surfaces. Ruled surfaces with two Diretrices. CYLINDROID –– both directrices are curves. CONOID –– one directrix
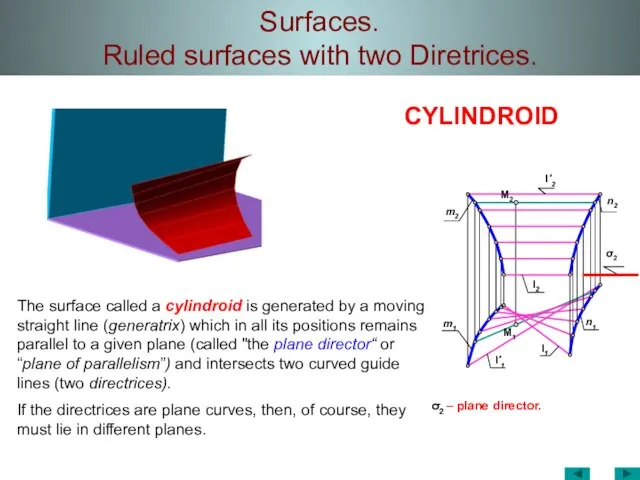
- 32. Surfaces. Ruled surfaces with two Diretrices. σ2 – plane director. l1 l'1 m1 M1 l2 M2
- 33. Surfaces. Ruled surfaces with two Diretrices. σ2 - plane director. х m2 n1 m1 σ2 σ2
- 34. Surfaces. Ruled surfaces with two Diretrices. σ1 - plane director. σ1 х σ1 m2 M1 n2
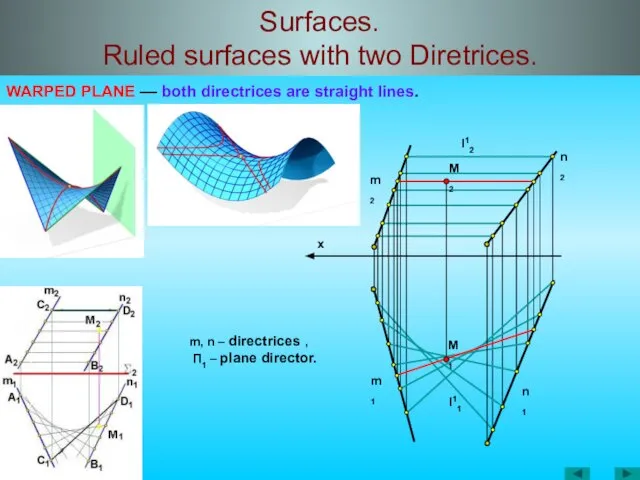
- 35. Surfaces. Ruled surfaces with two Diretrices. WARPED PLANE –– both directrices are straight lines. x m2
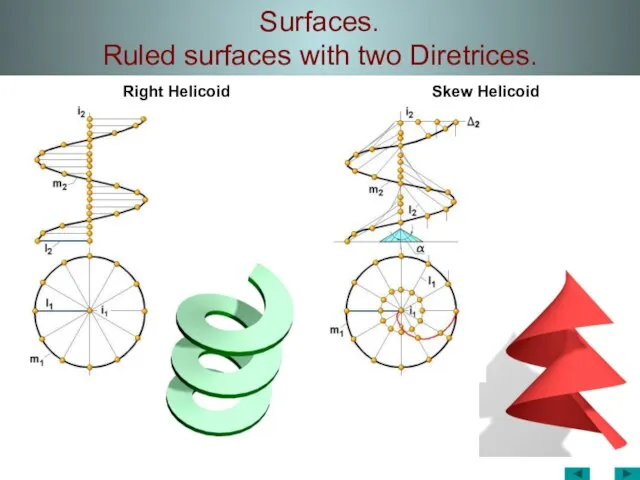
- 36. Surfaces. Ruled surfaces with two Diretrices. Right Helicoid Right Helicoid — ruled surface with a plane
- 37. Surfaces. Ruled surfaces with two Diretrices. Skew Helicoid Skew Helicoid – ruled surface where generatrix ℓ
- 38. Surfaces. Ruled surfaces with two Diretrices. Right Helicoid Skew Helicoid
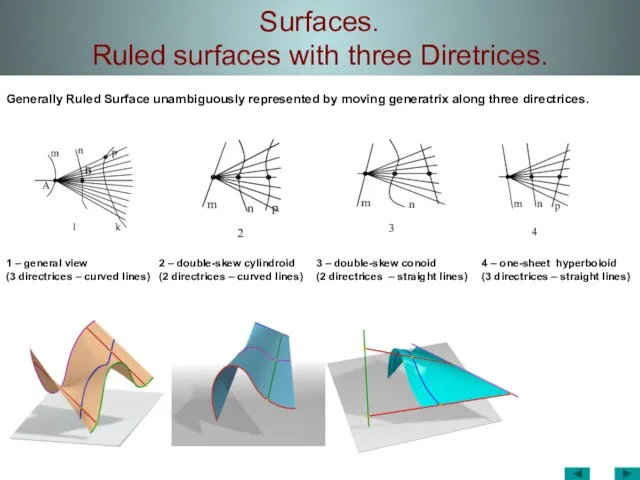
- 39. Surfaces. Ruled surfaces with three Diretrices. 1 – general view (3 directrices – curved lines) 2
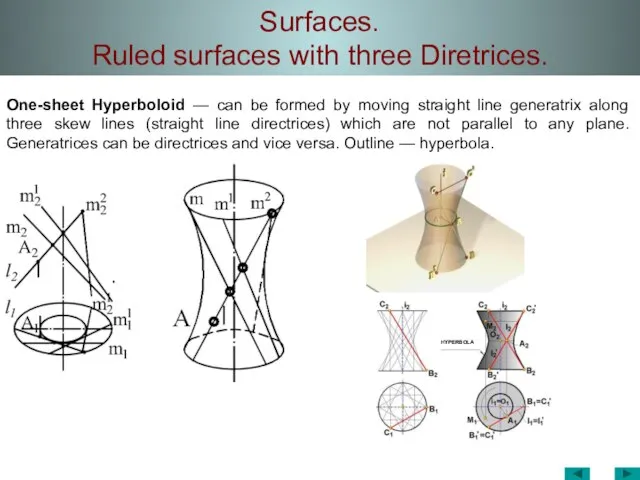
- 40. Surfaces. Ruled surfaces with three Diretrices. One-sheet Hyperboloid — can be formed by moving straight line
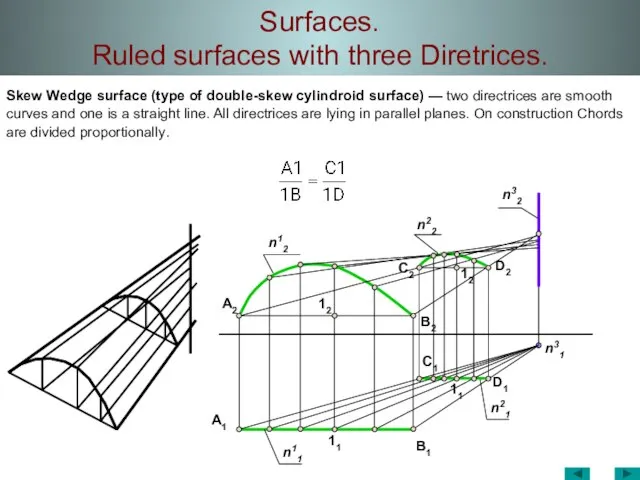
- 41. Surfaces. Ruled surfaces with three Diretrices. Skew Wedge surface (type of double-skew cylindroid surface) — two
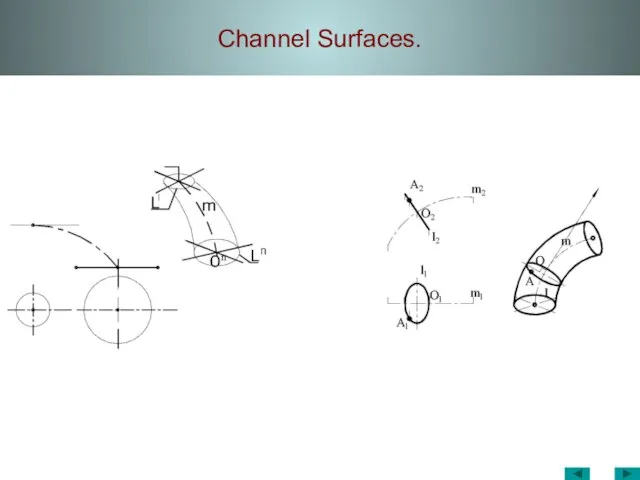
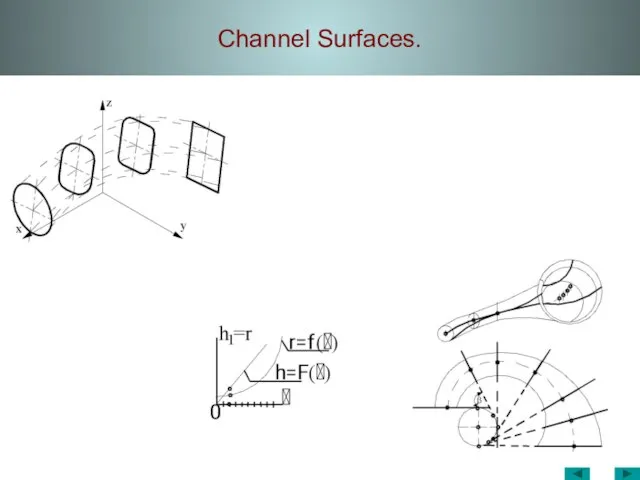
- 42. Channel Surfaces.
- 43. Channel Surfaces. On Ln L1 m
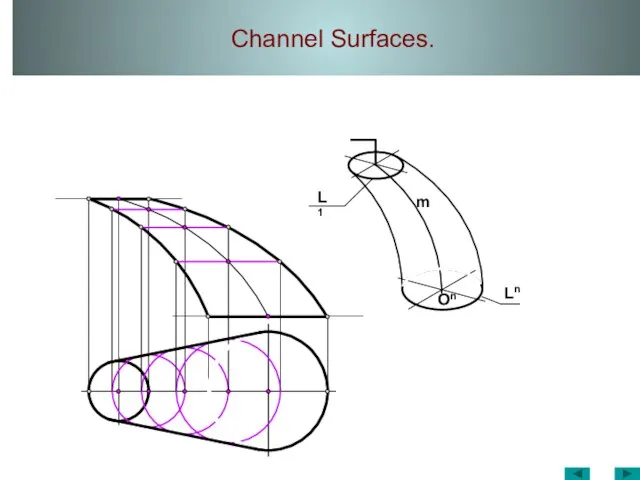
- 44. Channel Surfaces. A1 A m1 O1 l m2 l2 l1 O2 A2 O m
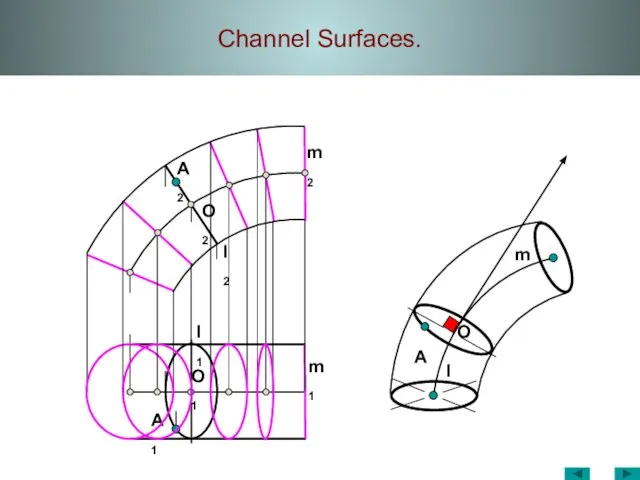
- 45. Channel Surfaces.
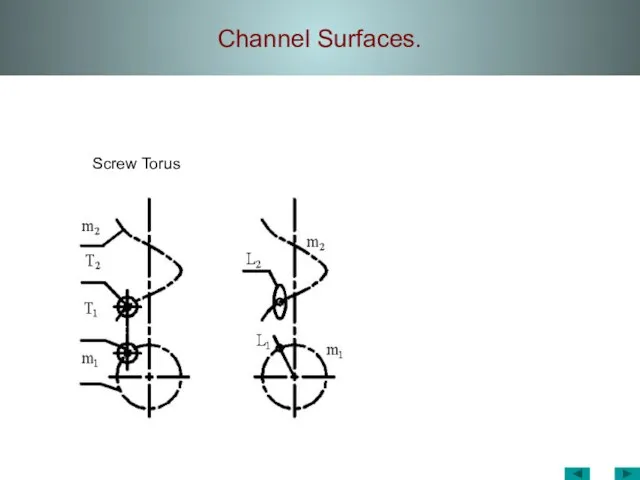
- 46. Channel Surfaces. Screw Torus
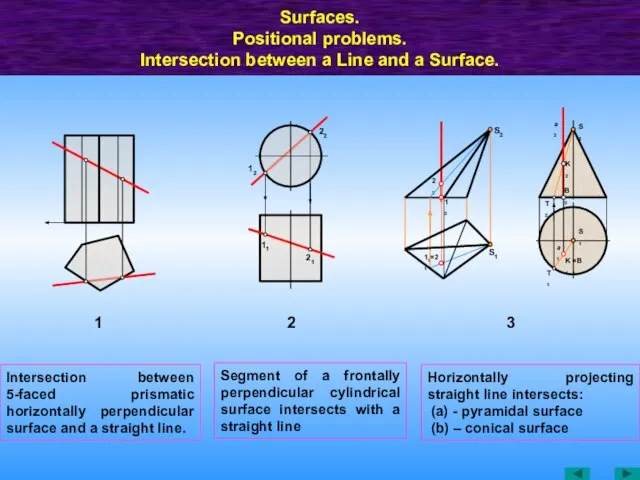
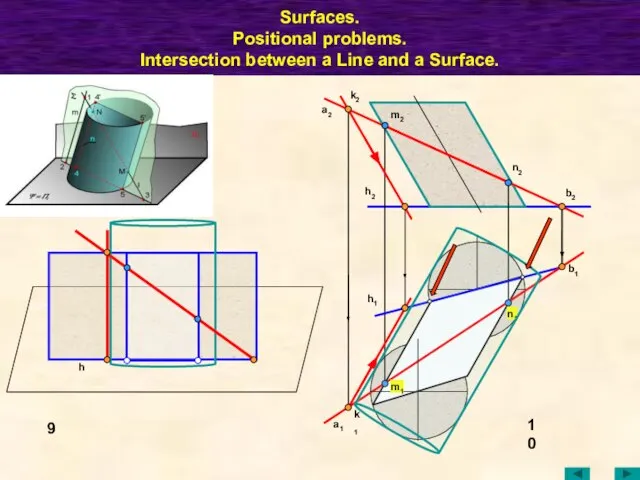
- 47. Surfaces. Positional problems. Intersection between a Line and a Surface. 1 11 21 2 12 22
- 48. Surfaces. Positional problems. Intersection between a Line and a Surface. M1 M2 A1 b2 A2 R1
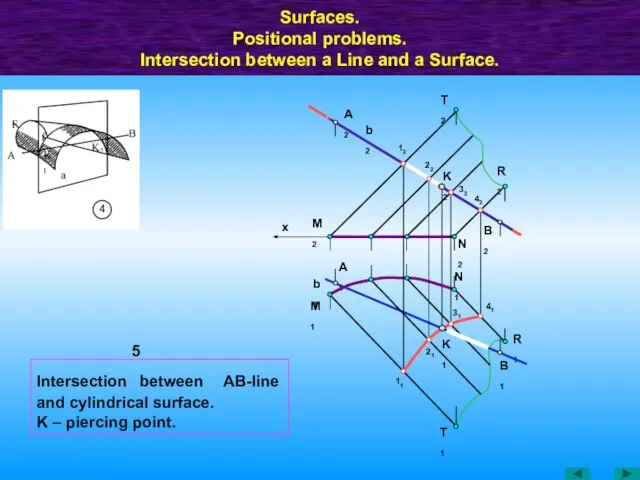
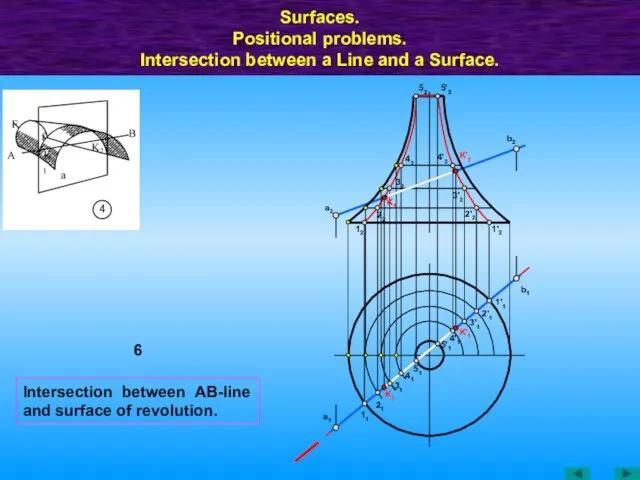
- 49. Intersection between АВ-line and surface of revolution. Surfaces. Positional problems. Intersection between a Line and a
- 50. Surfaces. Positional problems. Intersection between a Line and a Surface. 8 12 N2 11 x M1
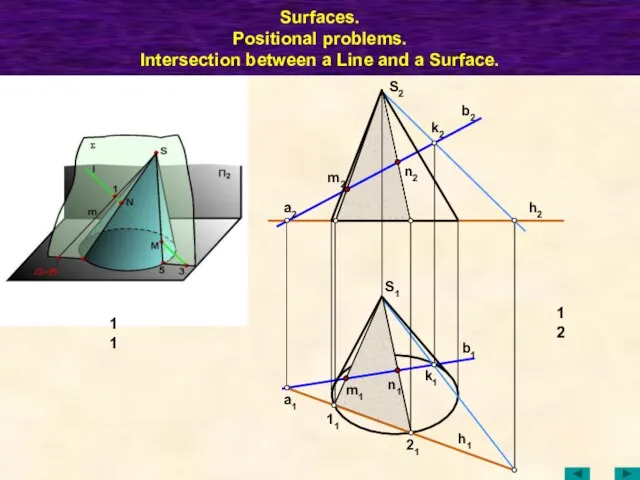
- 51. Surfaces. Positional problems. Intersection between a Line and a Surface. 10 a2 k2 a1 k1 h2
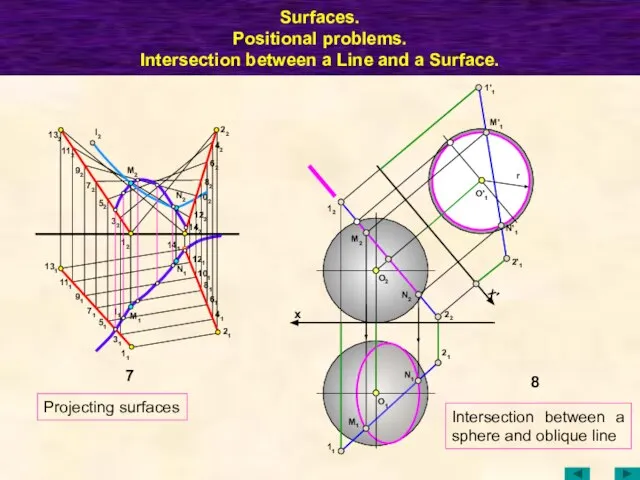
- 52. Surfaces. Positional problems. Intersection between a Line and a Surface. n1 12 m1 11 a1 21
- 53. Surfaces. Positional problems. Intersection between surfaces. Positional problems determine relative position and mutual belongings of objects
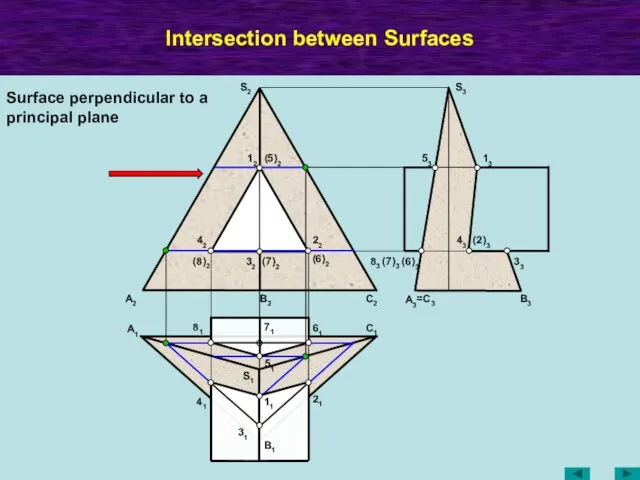
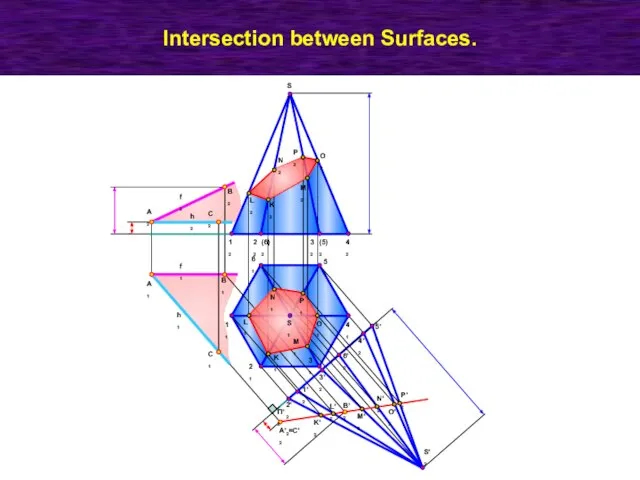
- 54. Intersection between Surfaces A2 A1 B2 C2 C1 B1 A3 =C3 B3 S2 S3 S1 12
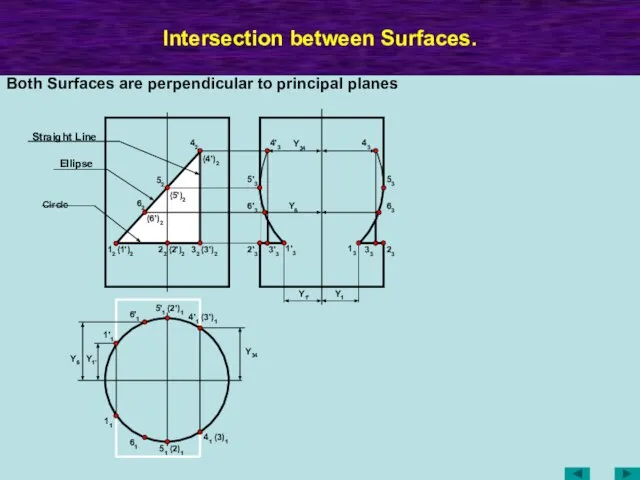
- 55. Intersection between Surfaces. Y34 12 (2')2 (3')2 42 (5')2 (4')2 32 22 (1')2 52 11 41
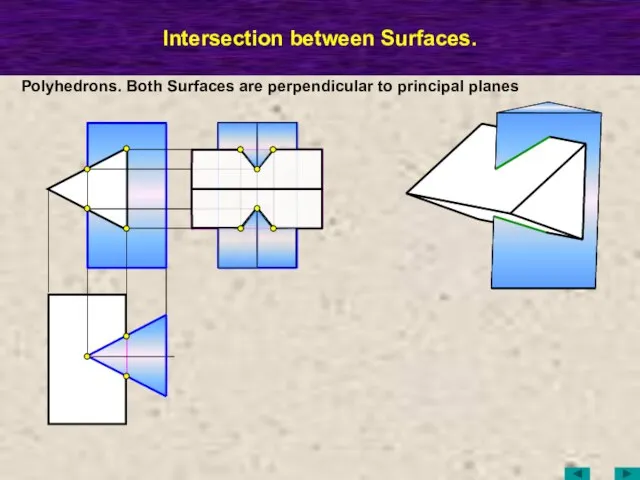
- 56. МТК Intersection between Surfaces. Polyhedrons. Both Surfaces are perpendicular to principal planes
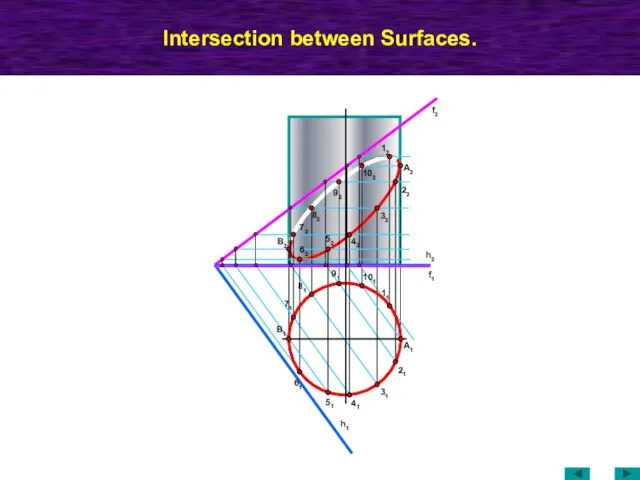
- 57. МТК Intersection between Surfaces. f2 h1 62 B1 22 32 42 52 72 f1 h2 11
- 58. Intersection between Surfaces. B2 A2 C2 C1 B1 A1 11 21 31 41 51 61 S1
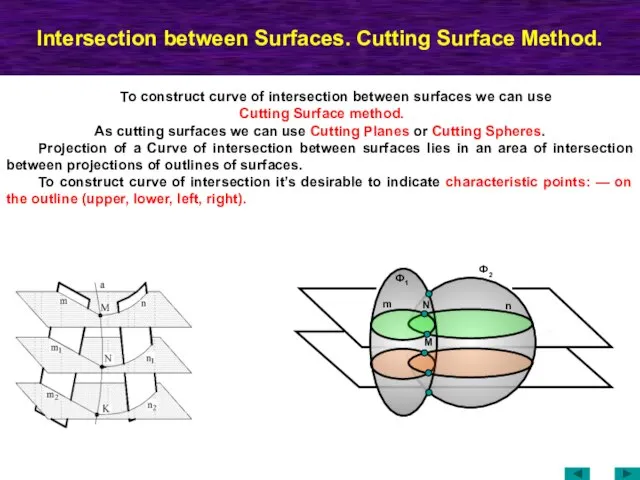
- 59. Intersection between Surfaces. Cutting Surface Method. To construct curve of intersection between surfaces we can use
- 60. Intersection between Surfaces. Cutting Plane Method. S2 (2')2 (3')2 42 (5')2 (4')2 32 22 52 (4')3
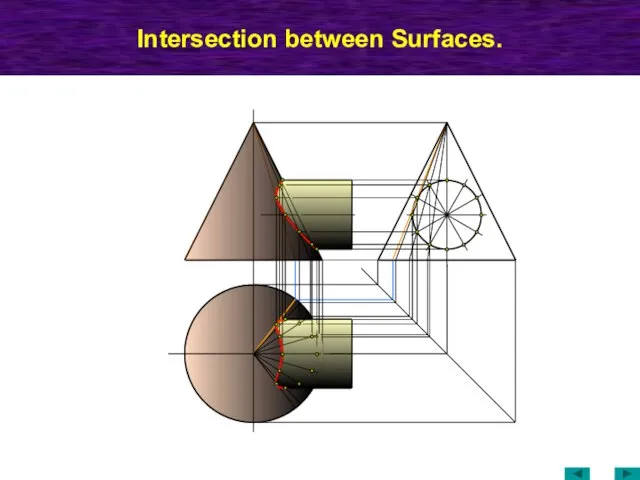
- 61. Intersection between Surfaces.
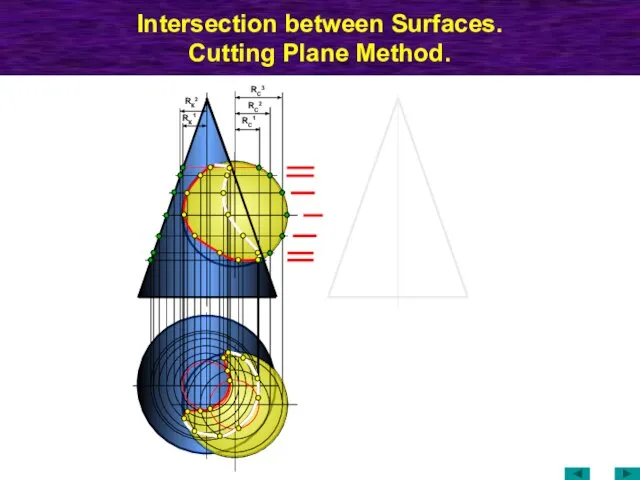
- 62. Intersection between Surfaces. Cutting Plane Method. RC1 RC2 RК1 RК2 RC3
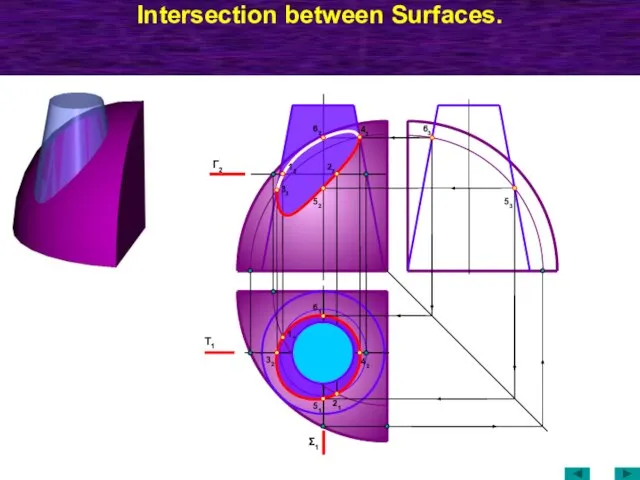
- 63. Intersection between Surfaces. Τ1 Γ2 21 11 42 32 Σ1 51 61 52 53 63 42
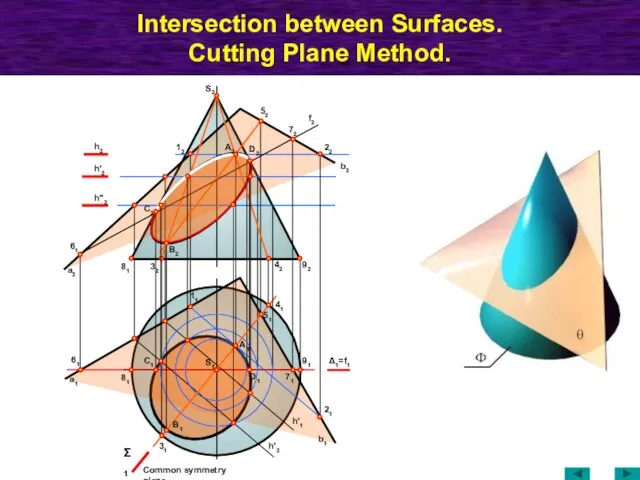
- 64. Intersection between Surfaces. Cutting Plane Method. а1 61 81 41 42 92 31 Σ1 Δ1=f1 72
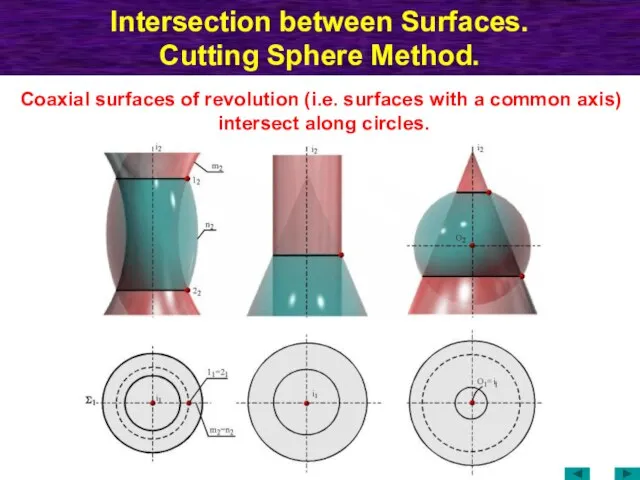
- 65. Intersection between Surfaces. Cutting Sphere Method. Coaxial surfaces of revolution (i.e. surfaces with a common axis)
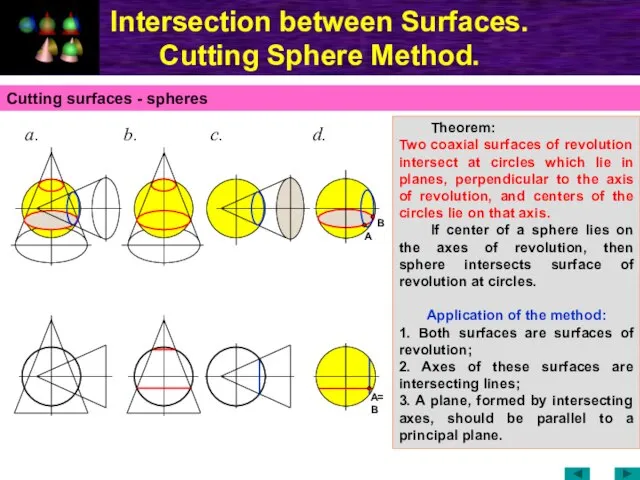
- 66. Intersection between Surfaces. Cutting Sphere Method. Cutting surfaces - spheres Theorem: Two coaxial surfaces of revolution
- 67. Intersection between Surfaces. Cutting Sphere Method. Algorithm how to construct curves of intersection between two surfaces
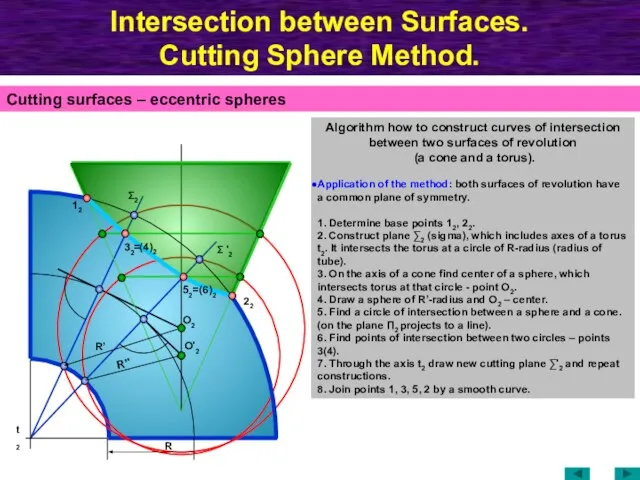
- 68. Intersection between Surfaces. Cutting Sphere Method. Cutting surfaces – eccentric spheres Algorithm how to construct curves
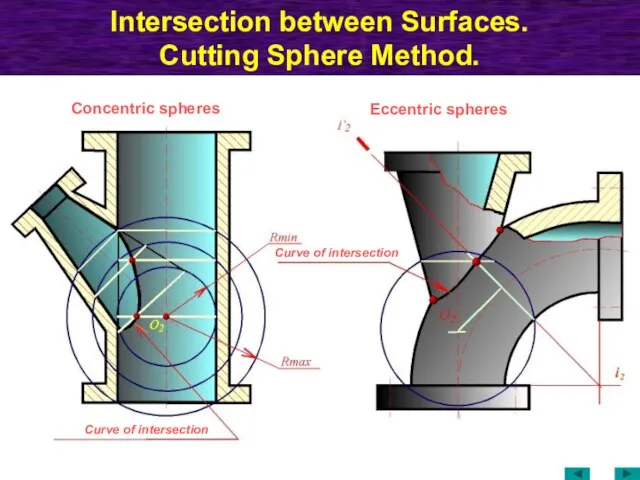
- 69. Intersection between Surfaces. Cutting Sphere Method. Curve of intersection Curve of intersection Concentric spheres Eccentric spheres
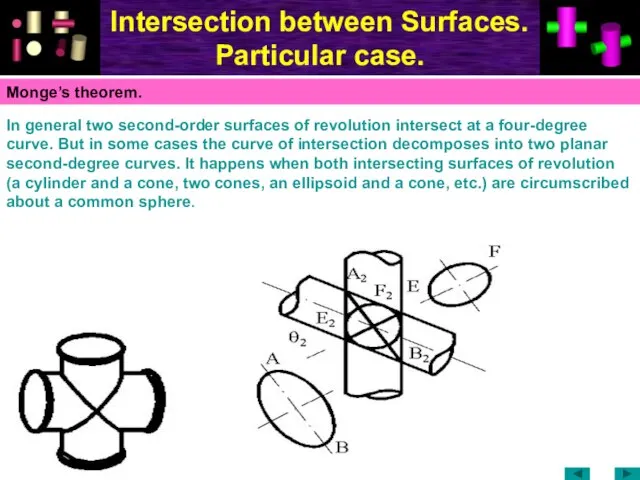
- 70. Intersection between Surfaces. Particular case. In general two second-order surfaces of revolution intersect at a four-degree
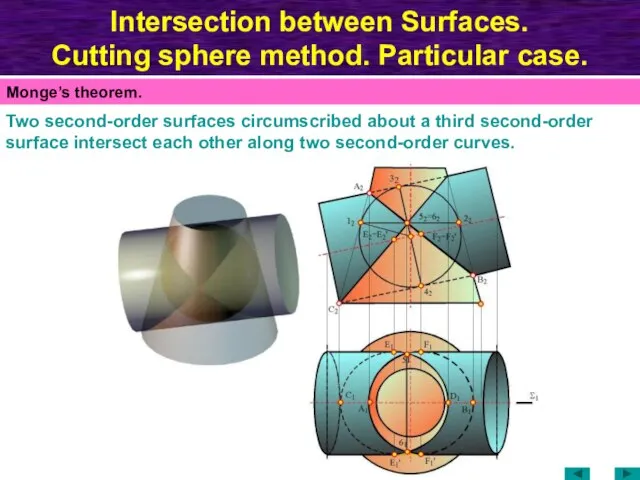
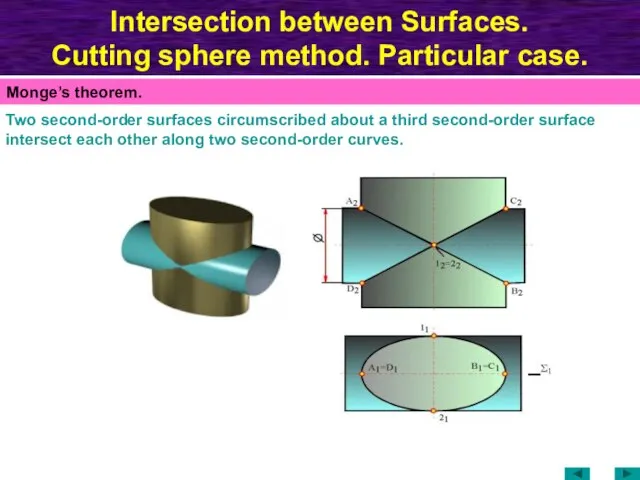
- 71. Intersection between Surfaces. Cutting sphere method. Particular case. Two second-order surfaces circumscribed about a third second-order
- 72. Intersection between Surfaces. Cutting sphere method. Particular case. Two second-order surfaces circumscribed about a third second-order
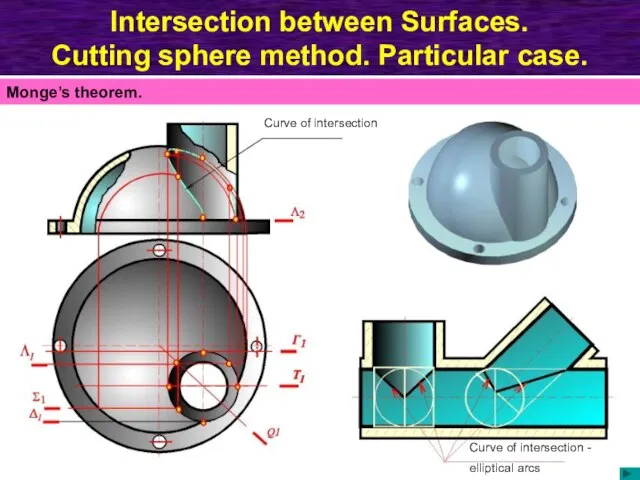
- 73. Intersection between Surfaces. Cutting sphere method. Particular case. Curve of intersection Curve of intersection - elliptical
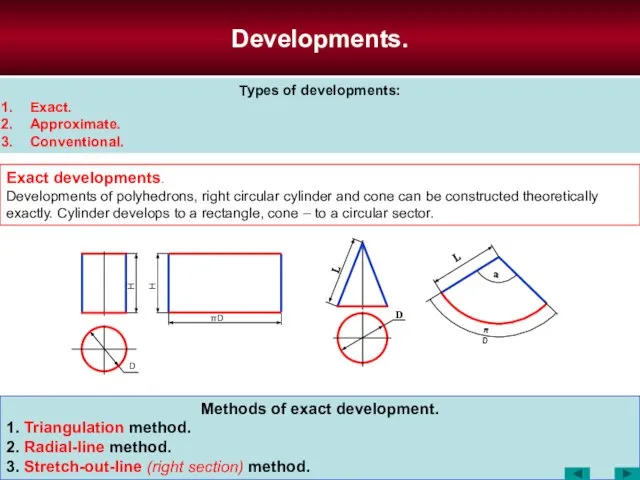
- 74. Developments. Properties of developments. Each point on the development corresponds to a single point of a
- 75. Methods of exact development. 1. Triangulation method. 2. Radial-line method. 3. Stretch-out-line (right section) method. Developments.
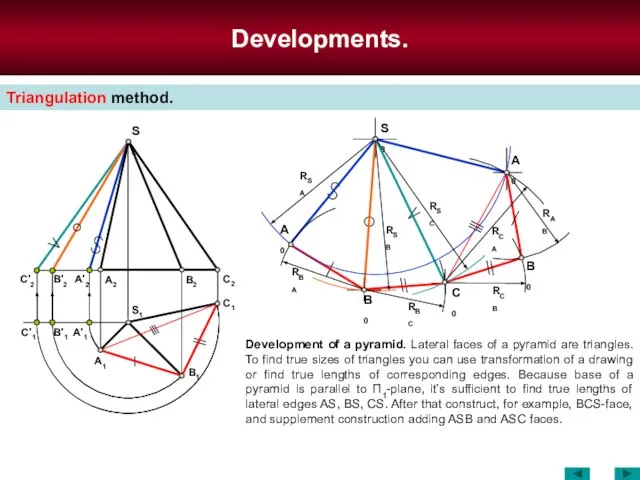
- 76. Developments. Triangulation method. Development of a pyramid. Lateral faces of a pyramid are triangles. To find
- 77. Developments. Radial Line method. C0 A1 A2 C0 A0 B0 D0 D1 C1 F1 B1 C2
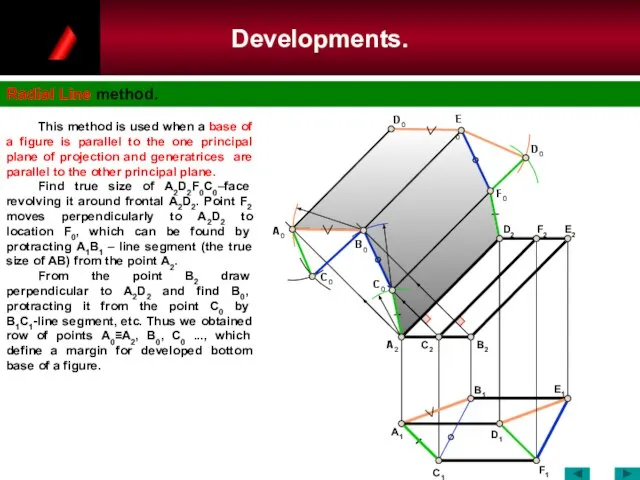
- 78. Developments. Stretch out Line method. This method is used when generatrices are parallel to a principal
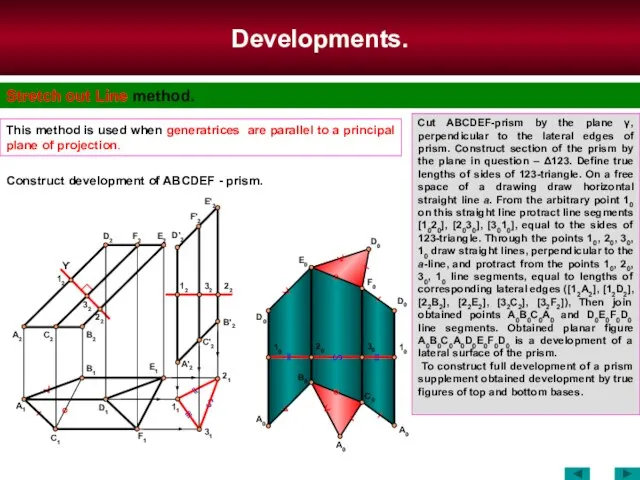
- 79. Development of a conical surface. Triangulation method. Substitute (approximate) the conical surface by polyhedral pyramidal surface.
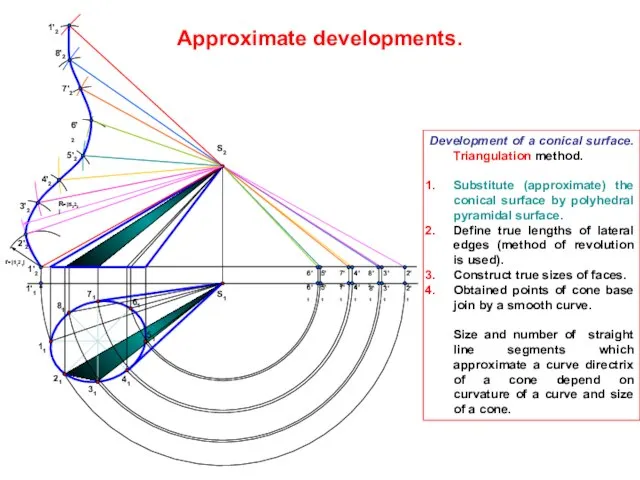
- 80. Conventional developments. Development of Toroidal surface— Zone Method Each parallel of a surface is spaced an
- 82. Скачать презентацию



















 Сагуны мясокомбинат. Коммерческое предложение от МТС
Сагуны мясокомбинат. Коммерческое предложение от МТС Customer Development. Магазин стикеров
Customer Development. Магазин стикеров Стратегия тактика поиска работы: основные понятия и характеристики. Лекция 6
Стратегия тактика поиска работы: основные понятия и характеристики. Лекция 6 Семейное право
Семейное право Урок окружающего мира1 класс
Урок окружающего мира1 класс Получение радиоактивных изотопов и их применение
Получение радиоактивных изотопов и их применение Презентация на тему Физкульт минутки для начальной школы
Презентация на тему Физкульт минутки для начальной школы  Каталог № 4 2010новинки и акции15 марта – 3 апреля
Каталог № 4 2010новинки и акции15 марта – 3 апреля Presentation Title
Presentation Title  Заграничный поход русской армии. Внешняя политика в 1813-1825 гг.
Заграничный поход русской армии. Внешняя политика в 1813-1825 гг. Презентация по английскому Конструкция To Be Going To 5 класс по УМК М.З. Биболетовой «Enjoy English – 5-6
Презентация по английскому Конструкция To Be Going To 5 класс по УМК М.З. Биболетовой «Enjoy English – 5-6 Что такое предпринимательство и бизнес
Что такое предпринимательство и бизнес Маникюр от Светланы
Маникюр от Светланы Help: настройка Visual Studio.Net длясоздания консоль-приложения на основе Intel C++ с применением OpenMP. Инструменты
Help: настройка Visual Studio.Net длясоздания консоль-приложения на основе Intel C++ с применением OpenMP. Инструменты Основы организационного дизайна
Основы организационного дизайна Самые ядовитые животные планеты
Самые ядовитые животные планеты Районный конкурс Школьная медиация глазами детей
Районный конкурс Школьная медиация глазами детей Решение уравнений и задач при помощи уравнений
Решение уравнений и задач при помощи уравнений Дисциплинарная и материальная ответственность работников. (Тема 4)
Дисциплинарная и материальная ответственность работников. (Тема 4) Поэма М.Ю. Лермонтова«Песня про царя Ивана Васильевича, молодогоопричника и удалого купца Калашникова»
Поэма М.Ю. Лермонтова«Песня про царя Ивана Васильевича, молодогоопричника и удалого купца Калашникова» Хакасия. Уйбатская степь
Хакасия. Уйбатская степь Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4.
Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4. Клубная система ОАО АСБ БЕЛАРУСБАНК для физических лиц
Клубная система ОАО АСБ БЕЛАРУСБАНК для физических лиц Духовность ?!
Духовность ?! RNWA. Представитель международной федерации скандинавской ходьбы
RNWA. Представитель международной федерации скандинавской ходьбы Опыт внедрения DIRECTUM в Новикомбанк
Опыт внедрения DIRECTUM в Новикомбанк Презентация на тему Охрана окружающей среды
Презентация на тему Охрана окружающей среды  Лучший день с мамой
Лучший день с мамой