Содержание
- 2. Introduction A problem of joint detection and estimation of parameters of faint space object streaks in
- 3. Models of signals Streak of the space object is determined by the vector Streak motion model
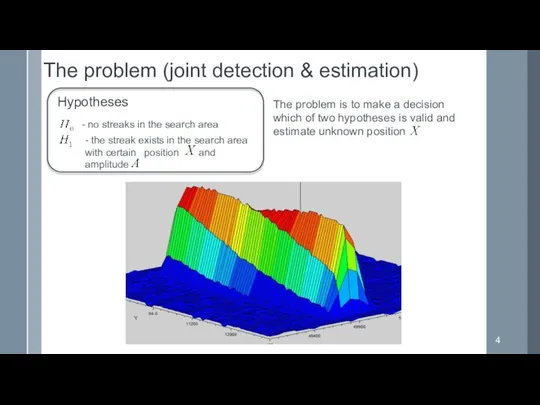
- 4. - no streaks in the search area - the streak exists in the search area with
- 5. – model profile values (calculated in advance) Sliding window rule (Moving average test) ), Algorithm: Stage
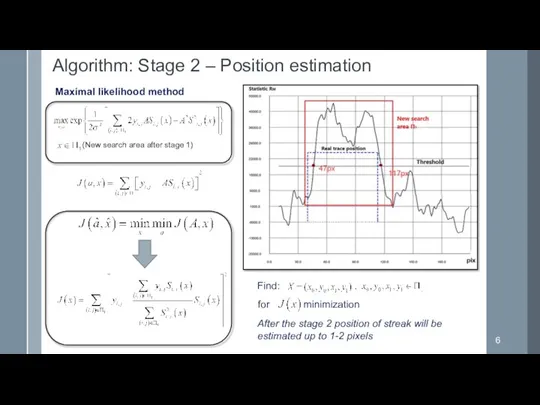
- 6. Maximal likelihood method Find: for minimization (New search area after stage 1) Algorithm: Stage 2 –
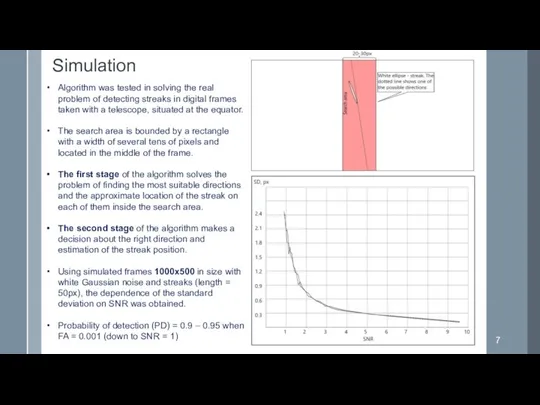
- 7. Simulation Algorithm was tested in solving the real problem of detecting streaks in digital frames taken
- 8. Simulation: real frames When operating with real frames it is crucial to get rid of strong
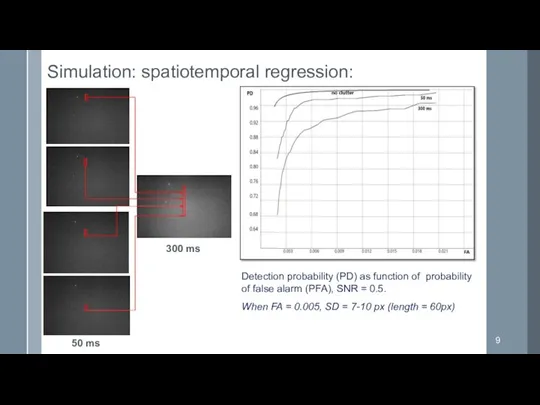
- 9. Simulation: spatiotemporal regression: Detection probability (PD) as function of probability of false alarm (PFA), SNR =
- 10. Conclusion and future work We proposed an effective two-stage algorithm which significantly reduces the number of
- 11. Acknowledgements I am grateful to Alexey E. Kolessa and Alexander G. Tartakovsky for setting the problem,
- 13. Скачать презентацию





 «Аспекты лидерства»
«Аспекты лидерства» ООО СПК «ЮНИТИ РЕ»
ООО СПК «ЮНИТИ РЕ» Школа 64. Традиции школы
Школа 64. Традиции школы Вводные слова и словосочетания
Вводные слова и словосочетания Презентация на тему Чем питаются животные (1 класс)
Презентация на тему Чем питаются животные (1 класс) Новогодние программы
Новогодние программы Электронный учебник на DVDи мультимедийное методическое пособие на CD для курса «Информатика и ИКТ»
Электронный учебник на DVDи мультимедийное методическое пособие на CD для курса «Информатика и ИКТ» Презентация на тему Корневище Клубень Луковица
Презентация на тему Корневище Клубень Луковица Познай Беларусь Белорусская кухня
Познай Беларусь Белорусская кухня Культура и религия
Культура и религия ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ
ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ Подготовка к региональному этапу всероссийской олимпиады школьников по обществознанию
Подготовка к региональному этапу всероссийской олимпиады школьников по обществознанию Социальные ценности и нормы
Социальные ценности и нормы Язык — душа народа!
Язык — душа народа! Сложное горячее блюдо
Сложное горячее блюдо Выбери цвет
Выбери цвет Презентация «Экология жилища» подготовлена по материалам журнала «Maxim» ученицей 9«А» класса ЦО 1685 Бариновой Дарьей Москва, 201
Презентация «Экология жилища» подготовлена по материалам журнала «Maxim» ученицей 9«А» класса ЦО 1685 Бариновой Дарьей Москва, 201 Hausratversicherung
Hausratversicherung Оценка ценных бумаг. Тема № 8
Оценка ценных бумаг. Тема № 8 Словообразование имен прилагательных (6 класс)
Словообразование имен прилагательных (6 класс) Русские народные песни
Русские народные песни Земельные ресурсы
Земельные ресурсы История, запечатленная в памятниках
История, запечатленная в памятниках Рівненський науково - виробничий центр стандартизації, метрології та сертифікації
Рівненський науково - виробничий центр стандартизації, метрології та сертифікації Кукла-мотанка. Забытая игрушка
Кукла-мотанка. Забытая игрушка Наша армия. Пограничные войска
Наша армия. Пограничные войска Урок – практикум. Подготовка и проведение.
Урок – практикум. Подготовка и проведение. Интегрированное занятиес дошкольниками «Правила безопасного перехода через дорогу»
Интегрированное занятиес дошкольниками «Правила безопасного перехода через дорогу»