Дифракция света

Принцип Гюйгенса-Френеля
2. При расчете амплитуды световых колебаний, возбуждаемых источником S0 в произвольной точке М, источник S0 можно заменить эквивалентной ему системой вторичных источников - малых участков ds любой замкнутой вспомогательной поверхности S, проведенной так, чтобы она охватывала источник S0 и не охватывала рассматриваемую точку М;
1 . Каждая точка среды, до которой доходит волна, является источником вторичных волн; огибающая этих волн дает положение волнового фронта в следующий момент времени;

4. Мощности вторичного излучения равных по площади участков волновой поверхности одинаковы;
3 . Вторичные источники когерентны S0 и между собой, поэтому возбуждаемые ими вторичные волны интерферируют при наложении;
5. Каждый вторичный источник излучает преимущественно в направлении внешней нормали к волновой поверхности в этой точке. Амплитуда dA колебаний, возбуждаемых в т. М вторичным источником задается соотношением:

где а - величина, пропорциональная амплитуде первичной волны в точках элемента ds;
f(α) - функция, зависящая от угла α, принимающая значения от 1 при α=0 до 0 при α≥π/2;
5. Если часть волновой поверхности перекрыта непрозрачным экраном, то вторичные волны излучаются только открытыми участками поверхности;
r - расстояние от элемента волновой поверхности ds до т. М.

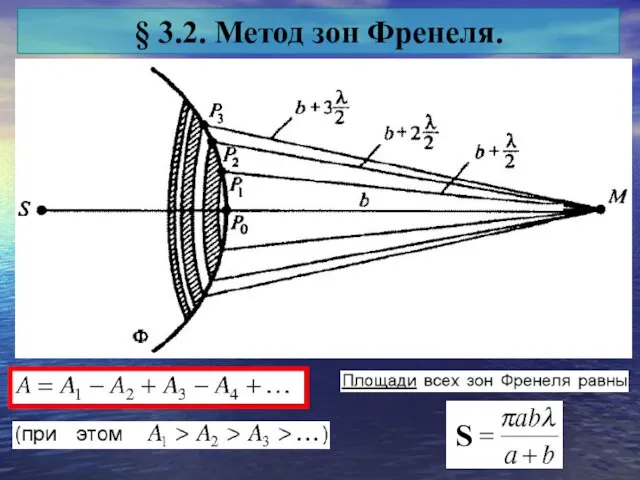
§ 3.2. Метод зон Френеля.

Различают два случая: дифракцию Френеля, или дифракцию в сходящихся лучах,
дифракцию Фраунгофера, или дифракцию в параллельных лучах.

В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся позади препятствия на конечном расстоянии от него.
Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света.
При дифракции Френеля на экране получается “дифракционное изображение” препятствия, а при дифракции Фраунгофера - “дифракционное изображение” удаленного источника света.

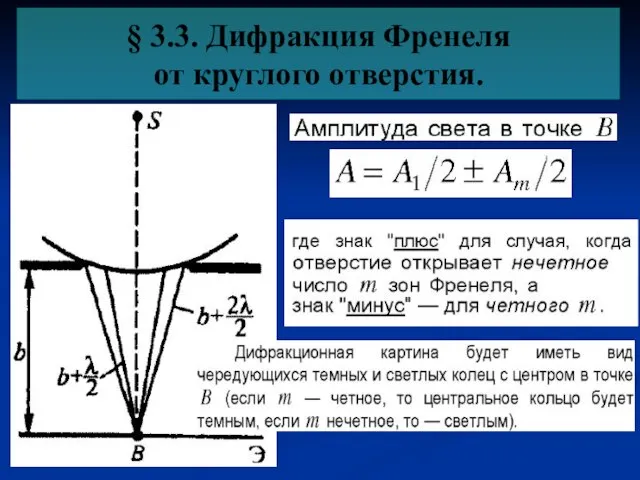
§ 3.3. Дифракция Френеля
от круглого отверстия.

§ 3.4. Дифракция Френеля
на диске.

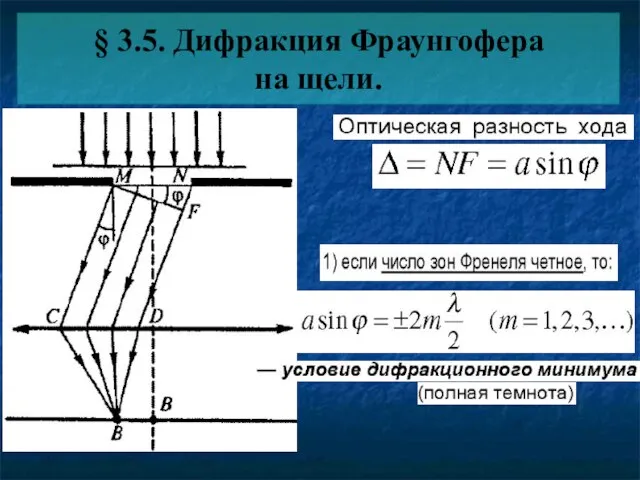
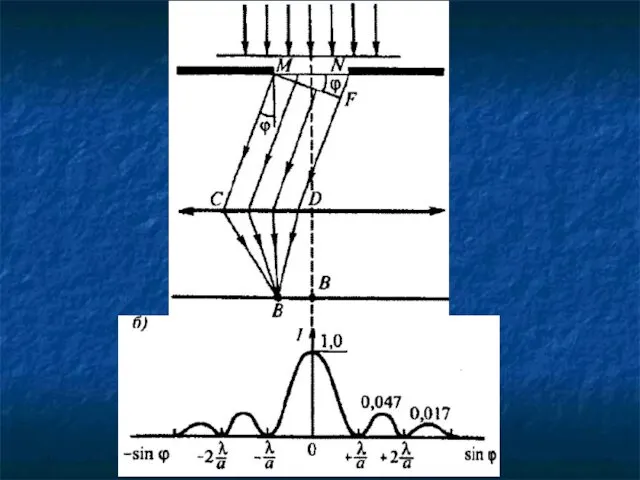
§ 3.5. Дифракция Фраунгофера
на щели.

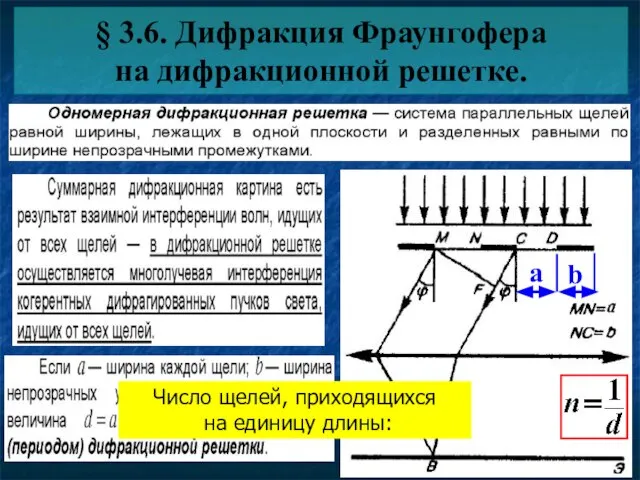
§ 3.6. Дифракция Фраунгофера
на дифракционной решетке.
Число щелей, приходящихся
на единицу длины:

Если решетка состоит из N щелей, то между двумя главными максимумами располагается N-1 дополнительных минимумов и N-2 дополнительных максимумов, создающих слабый фон.
Условие главных максимумов:
Условие главных минимумов:
Условие дополнительных минимумов:

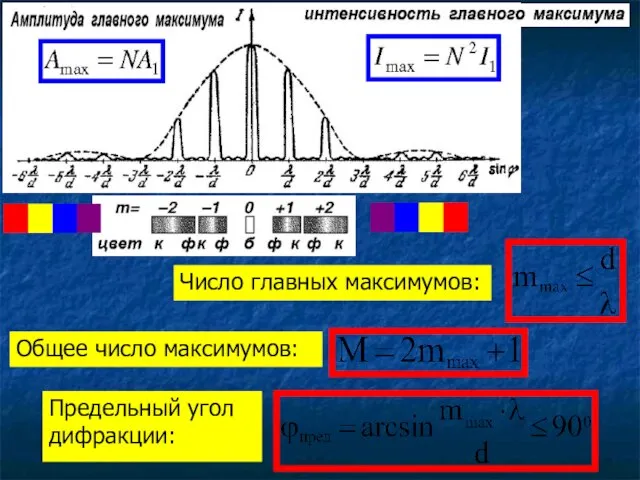
Число главных максимумов:
Общее число максимумов:
Предельный угол
дифракции:

§ 3.7. Графическое представление дифракционной картины.
Разность фаз колебаний:

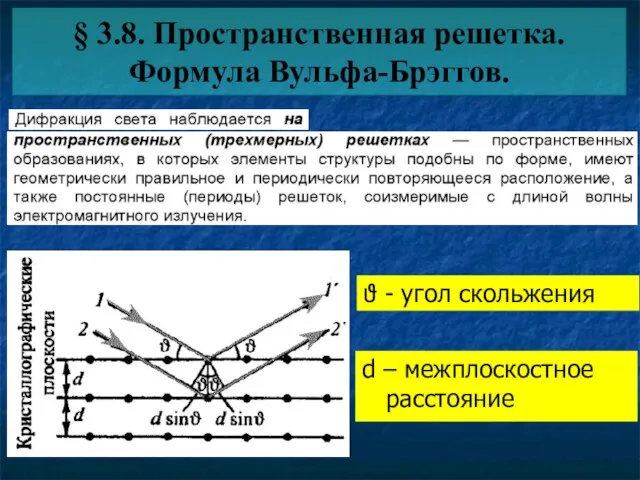
§ 3.8. Пространственная решетка. Формула Вульфа-Брэггов.
ϑ - угол скольжения
d – межплоскостное расстояние

Формула Вульфа-Брэггов.
ПРИМЕНЕНИЕ:
Максимумы интенсивности:

§ 3.9. Разрешающая способность спектрального прибора.
Разрешающая сила объектива :

по критерию Рэлея :