- Главная
- Разное
- Динамическая Декомпозиция волновых полей и Реконструкция модели среды при обработке данных ВСП.

Содержание
- 2. Содержание 1. Введение 2. Формулировка задач 3. Описание модели среды 4. Расчет лучей в двумерных градиентных
- 3. 1. Введение Как правило процессы обработки и интерпретации данных сейсморазведки эти процессы разделены во времени и
- 4. 2. Формулировка задач Для применения лучевого метода, являющегося высокочастотным приближением, модель должна удовлетворять ограничениям на максимальную
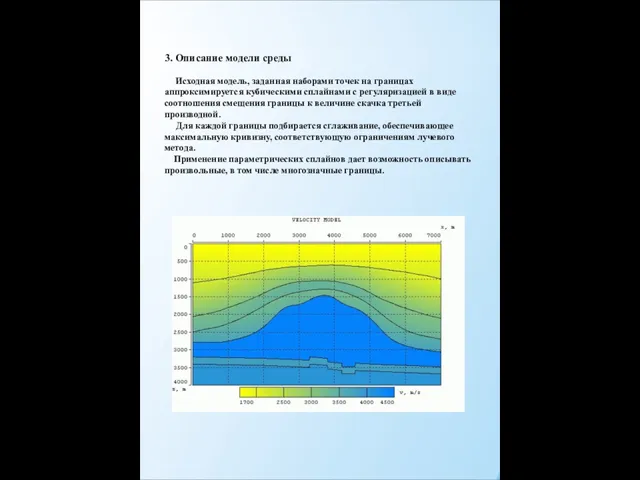
- 5. 3. Описание модели среды Исходная модель, заданная наборами точек на границах аппроксимируется кубическими сплайнами с регуляризацией
- 6. Для слежения лучей модель была разбита на квадратную сетку с шагом, внутри элементов которой градиент скоростей
- 7. Так как скорости меняются нелинейно, то слежение луча проводится пошагово. Направление и величина шага выбираются исходя
- 8. Учет преломления-отражения в точке пересечения хорды луча с границей производиться следующим образом: В точке пересечения проводится
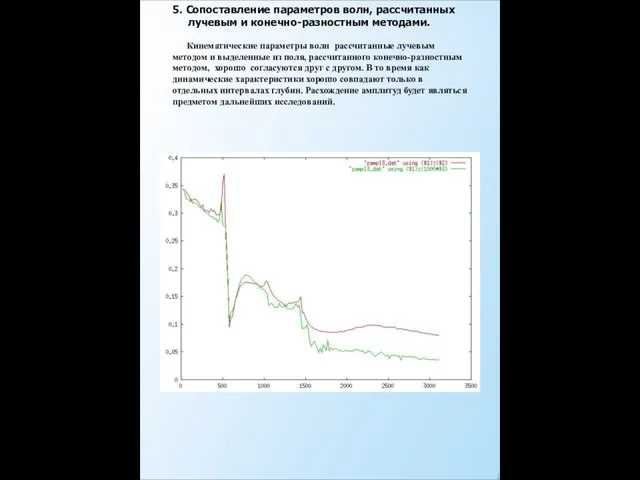
- 9. 5. Сопоставление параметров волн, рассчитанных лучевым и конечно-разностным методами. Кинематические параметры волн рассчитанные лучевым методом и
- 10. 6. Технология ДДР Технология обработки данных ВСП по методике ДДР состоит из нескольких процедур: 1. Построение
- 13. Скачать презентацию
Слайд 2
Содержание
1. Введение
2. Формулировка задач
3. Описание модели среды
4. Расчет лучей в двумерных
Содержание 1. Введение 2. Формулировка задач 3. Описание модели среды 4. Расчет лучей в двумерных

Слайд 3 1. Введение Как правило процессы обработки и интерпретации данных сейсморазведки эти
1. Введение Как правило процессы обработки и интерпретации данных сейсморазведки эти

Слайд 4 2. Формулировка задач
Для применения лучевого метода, являющегося высокочастотным приближением, модель
2. Формулировка задач Для применения лучевого метода, являющегося высокочастотным приближением, модель

Слайд 53. Описание модели среды
Исходная модель, заданная наборами точек на границах аппроксимируется
3. Описание модели среды Исходная модель, заданная наборами точек на границах аппроксимируется
Слайд 6 Для слежения лучей модель была разбита на квадратную сетку с шагом,
Для слежения лучей модель была разбита на квадратную сетку с шагом,

В случае линейной зависимости скоростей упругих волн от координат (градиент скоростей постоянен):
Слежение лучей.
Введем локальную систему координат , в которой скорость оказывается функцией только
.
В новой системе координат траектория луча представляет собой окружность :
где некоторые константы. Это уравнение окружности с координатами центра
ее радиус R имеет вид:
Здесь
4. Расчет лучей в градиентных средах с
криволинейными границами раздела
Для расчета в рамках лучевого метода кинематических и динамических характеристик волн разработаны численные методы, использующие локально-точные решения, что позволило получить простые устойчивые вычислительные процедуры. Основными из них являются программы слежения луча c учетом преломления- отражения в точке пересечения луча с границей и расчета динамических характеристик волн.
- параметр луча
- угол выхода луча из начальной точки
Слайд 7Так как скорости меняются нелинейно, то слежение луча проводится пошагово. Направление и
Так как скорости меняются нелинейно, то слежение луча проводится пошагово. Направление и

где
(i=0,1,….N) ,
- начальная точка i-ой хорды
-
скорость продольной волны
-
модуль градиента скоростей
-
направление касательной к траектории луча
-
направление градиента скоротей
Направляющий угол первой хорды равен , где - начальный угол, под которым был запущен луч.
Каждая из последующих хорд поворачивается на угол относительно предыдущей против часовой стрелки, если проекция вектора градиента на ось Z больше нуля и в противоположном направлении в противном случае. Касательная к лучу поворачивается от точки к точке в том же направлении и на тот же угол, как и хорда.
Координаты концов хорд вычисляются по следующим формулам:
В том случае, когда величина превышает /2 выполняется пересчет по формуле
. Т.е. при любых параметрах среды шаг по лучу не может быть больше чем половина длины элемента сетки.
Слайд 8Учет преломления-отражения в точке пересечения хорды луча с границей производиться следующим образом:
В
Учет преломления-отражения в точке пересечения хорды луча с границей производиться следующим образом:
В

рефракции падающей волны -ого типа , и в точке встречи - вектор
касательной к границе и вектор нормали к границе блока (внешняя нормаль).
Вектор рефракции преломленной или отраженной волны , где
Расчет динамических характеристик волн.
Для расчета амплитуд в каждом приемнике по известной траектории соответствующего луча использовалась формула :
Где :
коэффициент преломления отражения луча на i-той границе
n – число границ, пересекаемых волной
углы падения и отражения (преломления) на границе
сокости на луче до и после пересечения i-той границы
- соответствующие плотности.
L(M) – геометрическое расхождение лучевой трубки
Для расчета геометрического расхождения пускались дополнительные лучи с начальными углами a+da и a-da, где а – начальный угол луча, а da – небольшое приращение. Геометрическое расхождение определялось как отношение диаметров лучевой трубки (растояния между боковыми лучами) вблизи источника и на скважине .
Слайд 95. Сопоставление параметров волн, рассчитанных лучевым и конечно-разностным методами.
Кинематические параметры волн
5. Сопоставление параметров волн, рассчитанных лучевым и конечно-разностным методами. Кинематические параметры волн
Слайд 10 6. Технология ДДР
Технология обработки данных ВСП по методике ДДР состоит
6. Технология ДДР Технология обработки данных ВСП по методике ДДР состоит


 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов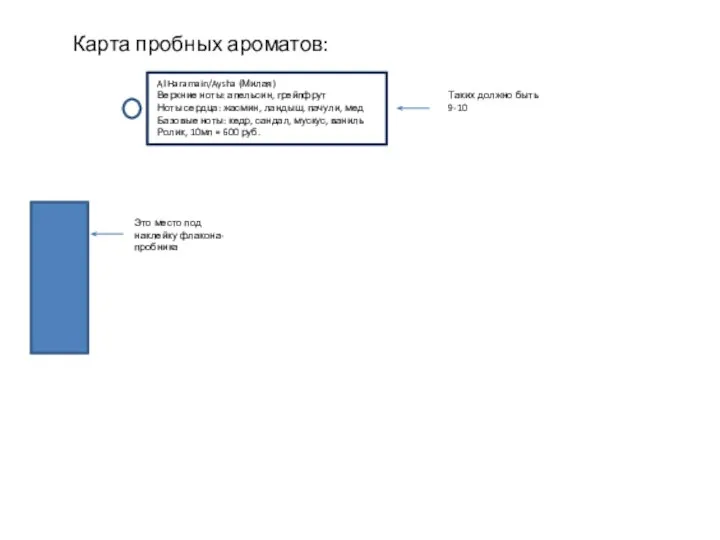 Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой