ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ

1. Теорема Бернулли: условия применимости
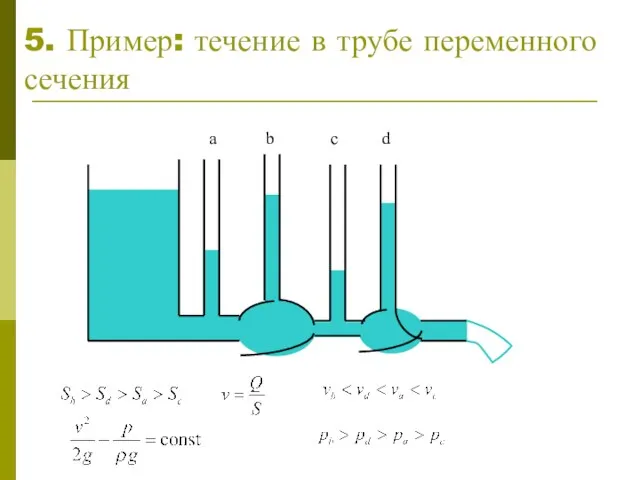
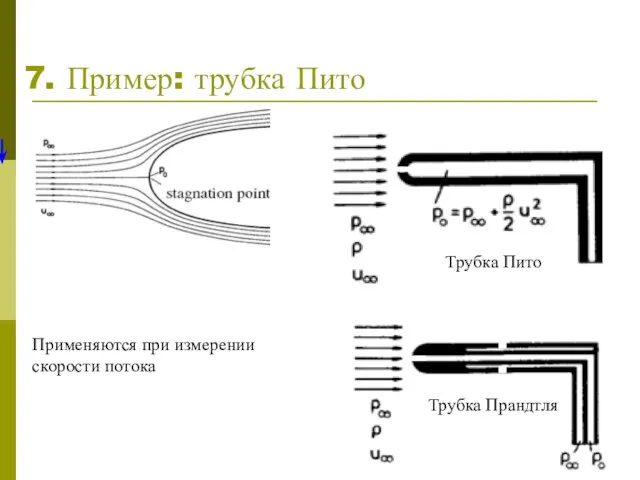
Теорема Бернулли – результат применения теоремы об изменении кинетической энергии к установившемуся движению жидкости. Это – основная теорема гидродинамики, имеющая многочисленные приложения при изучении течения воды в реках, каналах, трубах, при исследовании действия воды в водяных двигателях и т. д.
Теорема Бернулли имеет дело с идеальной жидкостью:
1) Несжимаемой
2) Невязкой
ВАЖНО: Работа внутренних сил в идеальной жидкости равна нулю!
Теорема Бернулли имеет дело с установившемся течением:
в каждой точке пространства, наполненного жидкостью, явления не изменяются с течением времени; направление и величина скорости в этой точке, величина давления у этой точки остаются постоянными во все время движения.

2. Теорема Бернулли: измене-ние кинетической энергии
Изменение кинетической энергии за время dt
Q –объемный расход жидкости [м3/c]
– плотность жидкости [кг/м3]

3. Теорема Бернулли: работа внешних сил
1) Работа сил тяжести
2) Работа сил давления
3) Работа сил со стороны стенок трубы равна нулю
Предполагается, что трения жидкости о стенки нет, значит силы нормальны к стенке. Скорости частиц жидкости касательны к стенке. Скалярное произведение есть ноль.

4. Теорема Бернулли: результат
При установившемся движении несжимаемой жидкости сумма геометрической, скоростной и пьезометрической высот остается неизменной для частиц одной и той же трубки тока.
высота, на которую поднимается тело, брошенное вверх со скоростью
высота столба жидкости с давлением p у основания столба

5. Пример: течение в трубе переменного сечения
a
b
c
d

6. Пример: истечение из сосуда
Если
Теорема Торичелли (1644)
S1
S2
К-т сжатия потока

7. Пример: трубка Пито
Трубка Пито
Трубка Прандтля
Применяются при измерении скорости потока

8. Пример: трубка Вентури
Применяются при измерении расхода жидкости в трубе
S1
S1
S2
S2

9. Теорема о вириале
- среднее за время
Левая часть обращается в ноль если выполнено одно из условий
Интервал не ограничен, а функция ограничена
Движение периодическое с периодом
вириал системы
При выполнении условий 1 или 2 среднее за время значение кинетической энергии равно ее вириалу

10. Пример: замкнутая гравитационная система
Теорема о вириале
Сохранение энергии
Указывает в какой пропорции начальная энергия «делится в среднем» между кинетической и потенциальной энергией во время движения замкнутой гравитационной системы
Задача : пусть
тогда

11. Пример: упругая цепочка
- потенциальная энергия системы