ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ

1. Момент количеств движения материальной системы
Моментом количеств движения системы относительно центра О называется сумма моментов (главный момент) количеств движения всех материальных точек, входящих в систему, относительно того же центра:
Координатная запись в проекциях на оси системы координат Oxyz
- масса i-ой точки
- скорость i-ой точки
- радиус-вектор i-ой точки с началом в центре O
Компонента вектора количества движения системы характеризует поступательное движении систему в направлении оси
Компонента момента количеств движения характеризует вращательное движение системы относительно оси

2. Момент количеств движения вращающегося твердого тела
Элемент M массы dm движется по окружности радиуса hz
Скорость движения
Количество движения
Момент количества движения
Интеграл Iz зависит только от распределения масс внутри тела и не зависит от его кинематического состояния. Он называется моментом инерции тела относительно оси z.
Момент количеств движения твердого тела, вращающегося относительно неподвижной оси равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

3. Примеры вычисления момента инерции
1) Момент инерции однородного стержня относительно оси, проходящей перпендикулярно стержню через его конец.
1) Момент инерции однородного цилиндра относительно его оси.

4. Связь с моментом, взятым относительно центра масс
Теорема
Моменты количеств движения и главные моменты сил взятые относительно произвольного центра O и центра масс С системы
Радиус векторы и скорости материальных точек и центра масс
Радиус-векторы и скорости относительно центра масс
Свойства центра масс
1)
2)

5. Пример применения
Задача: Найти момент количеств движения полого диска, катящегося без скольжения относительно неподвижной точки О

6. Теорема об изменении момента количеств движения
Теорема. Производная по времени вектора момента количеств движения системы материальных точек, вычисленная относительно неподвижного центра, равна главному моменту всех внешних сил относительно того же центра.
+

1. Внутренние силы непосредственно не влияют на изменение момента количеств движения материальной системы (они могут оказать косвенное влияние через внешние силы).
2. Если главный момент всех внешних сил относительно некоторого неподвижного центра равен нулю, то момент количества движения материальной системы относительно этого центра остается постоянным по величине и направлению.
закон сохранения момента количеств движения
3. Если главный момент всех внешних сил относительно некоторой неподвижной оси равен нулю, то момент количеств движения материальной системы относительно этой оси остается постоянным.
7. Следствия

8. Какие силы исключаются в уравнении моментов?
При записи уравнения моментов относительно некоторой оси исключаются
Все внутренние силы
Те внешние силы, момент которых относительно оси равен нулю, т.е. а) силы параллельные оси
б) силы, чья линия действия пересекает ось
Выбор оси зависит от нас. При удачном выборе можно достигнуть исключения значительного числа внешних сил, упростив тем самым уравнение моментов

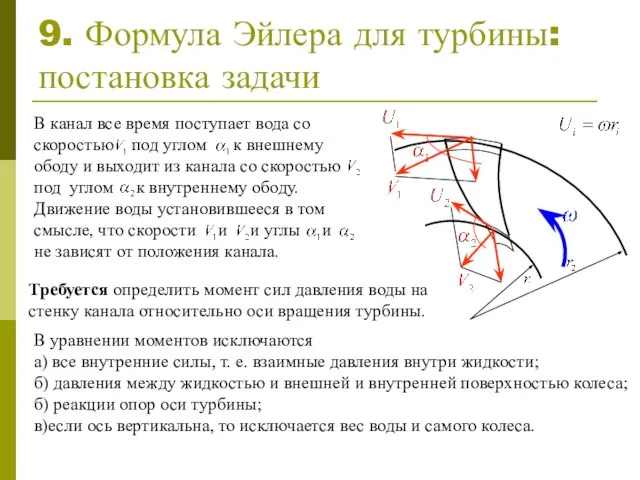
9. Формула Эйлера для турбины: постановка задачи
В уравнении моментов исключаются
а) все внутренние силы, т. е. взаимные давления внутри жидкости;
б) давления между жидкостью и внешней и внутренней поверхностью колеса;
б) реакции опор оси турбины;
в)если ось вертикальна, то исключается вес воды и самого колеса.
Требуется определить момент сил давления воды на стенку канала относительно оси вращения турбины.

9. Формула Эйлера для турбины: вывод
1) Изменение момента количеств движения за время dt
2) Действующие силы: реакция стенок канала
объем жидкости, протекающей через канал в единицу времени

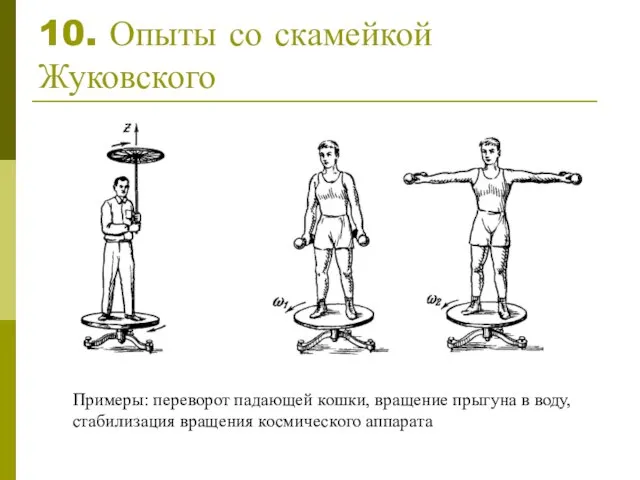
10. Опыты со скамейкой Жуковского
Примеры: переворот падающей кошки, вращение прыгуна в воду, стабилизация вращения космического аппарата

11. ДУ вращения твердого те-ла вокруг неподвижной оси
Замечание: При вычислении главного момента всех внешних сил относительно оси вращения нужно учитывать, что реакции идеальных (без трения) опор в уравнение не войдут, так как линии их действия пересекают ось вращения. Если же опоры создают моменты трения, то их необходимо учитывать.
Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу.
Полная аналогия с 3-м законом Ньютона
Момент инерции тела представляет меру его инерции во вращательном движении.

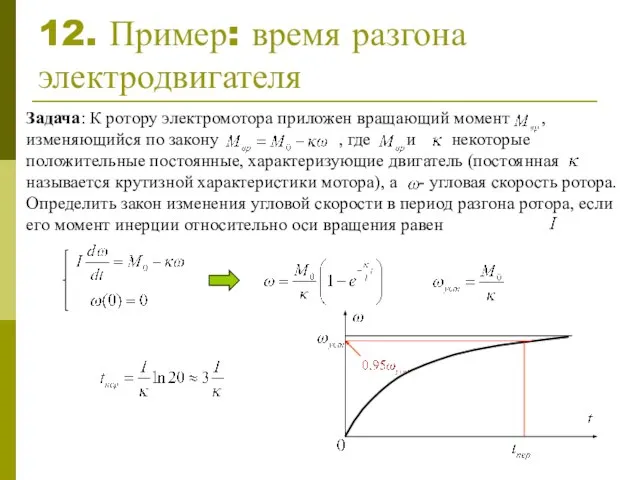
12. Пример: время разгона электродвигателя
Задача: К ротору электромотора приложен вращающий момент ,
изменяющийся по закону , где и некоторые положительные постоянные, характеризующие двигатель (постоянная называется крутизной характеристики мотора), а - угловая скорость ротора. Определить закон изменения угловой скорости в период разгона ротора, если его момент инерции относительно оси вращения равен

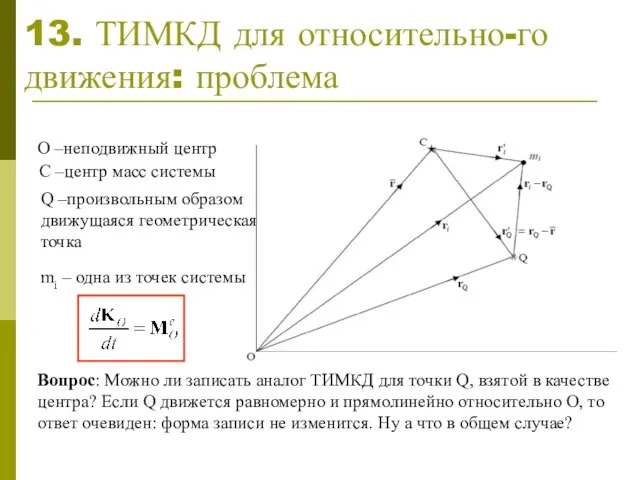
13. ТИМКД для относительно-го движения: проблема
О –неподвижный центр
С –центр масс системы
Q –произвольным образом движущаяся геометрическая точка
mi – одна из точек системы
Вопрос: Можно ли записать аналог ТИМКД для точки Q, взятой в качестве центра? Если Q движется равномерно и прямолинейно относительно О, то ответ очевиден: форма записи не изменится. Ну а что в общем случае?