Содержание
- 2. Мастер подключения презентации к уроку. S T O P Дальнейший просмотр возможен только при наличии соответствующих
- 3. Представим себе нить в форме окружности. Разрежем её и растянем за концы. Понятие длины окружности. Тонкая
- 4. Периметр любого вписанного в окружность многоугольника является приближённым значением длины окружности. При увеличении числа сторон правильный
- 5. O1 Свойство длины окружности. Отношение длины окружности к её диаметру есть одно и то же число
- 6. По свойству пропорции Доказательство: 1) Впишем в каждую окружность правильный n-угольник. Если число сторон неограниченно увеличивать,
- 7. Число «пи». Вывод формулы длины окружности. Из свойства длины окружности следует . что есть число постоянное
- 8. Верхушка головы - где 1,7м рост человека. Ноги прошли путь , где R радиус земного шара.
- 9. Обычно отвечают, что промежуток будет тоньше волоса. Задача 2. Если обтянуть земной шар по экватору проволокой
- 10. № 1104(а). Найти длину окружности описанной около правильного треугольника со стороной а. Выразите R через а.
- 11. R O R H Дано: △ АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a. №
- 12. № 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием Из △ВОН: BО2=OH2+BH2=R2= А
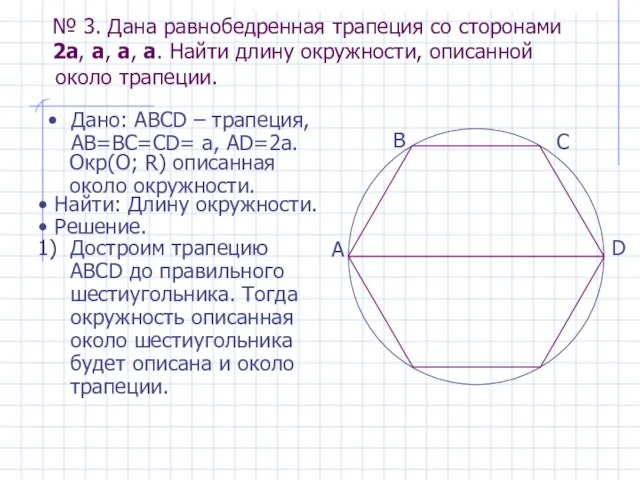
- 13. № 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной Дано:
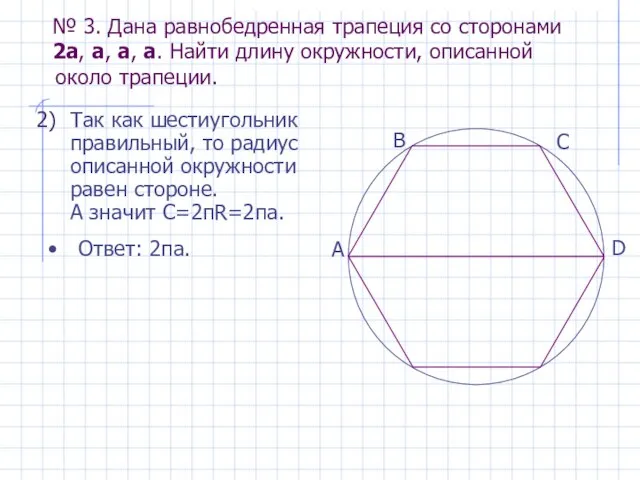
- 14. Так как шестиугольник правильный, то радиус описанной окружности равен стороне. А значит C=2πR=2πa. № 3. Дана
- 15. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ Сформулируйте основное свойство длины окружности. На чём основывается его доказательство? Как вычисляется длина
- 16. Домашнее задание Вопросы 8-9(стр. 270). №1108, №1105(а).
- 18. Скачать презентацию












 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве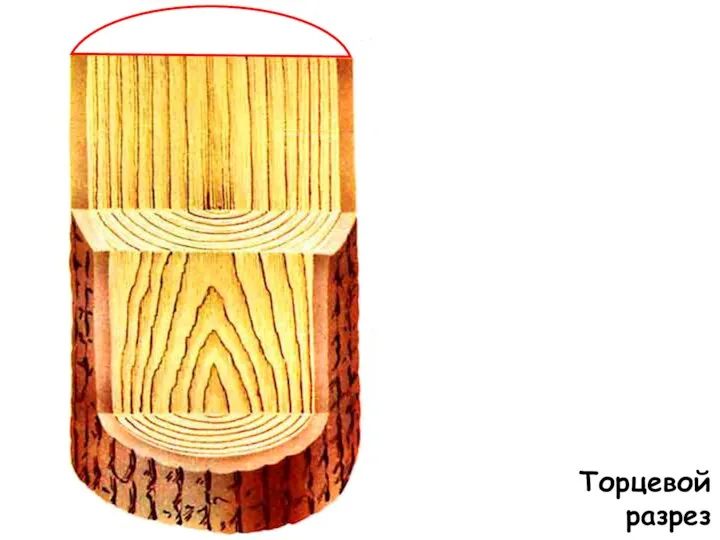 Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства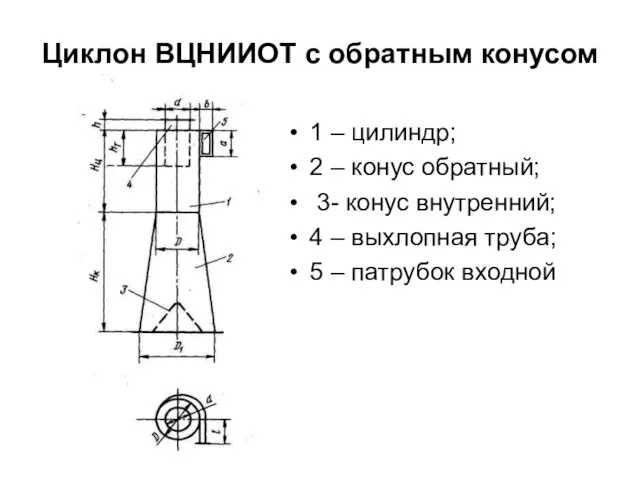 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)