Содержание
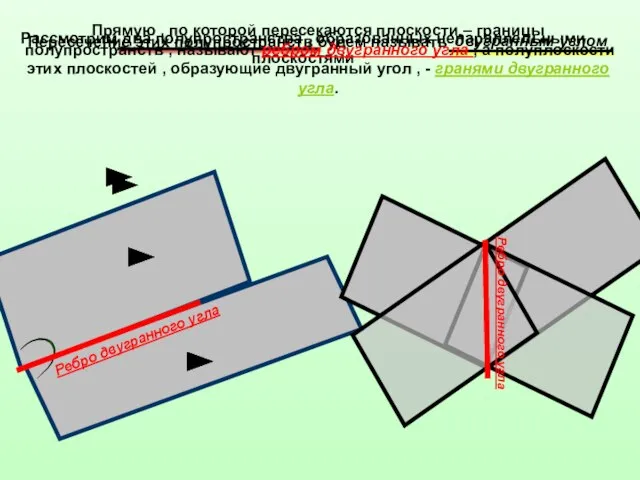
- 2. Рассмотрим два полупространства , образованных непараллельными плоскостями Пересечение этих полупространств будем называть двугранным углом Прямую ,
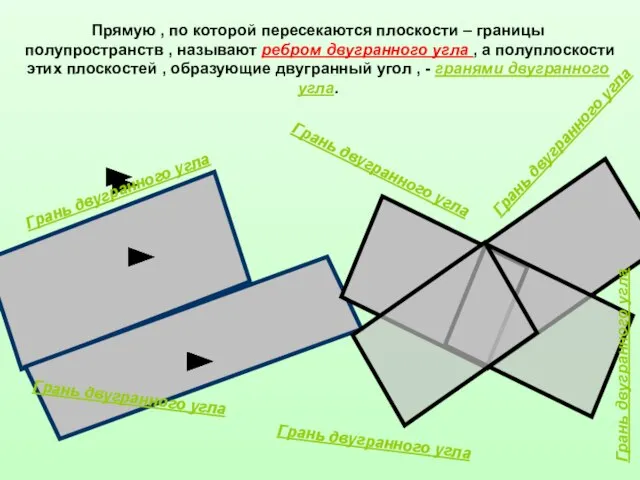
- 3. Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а
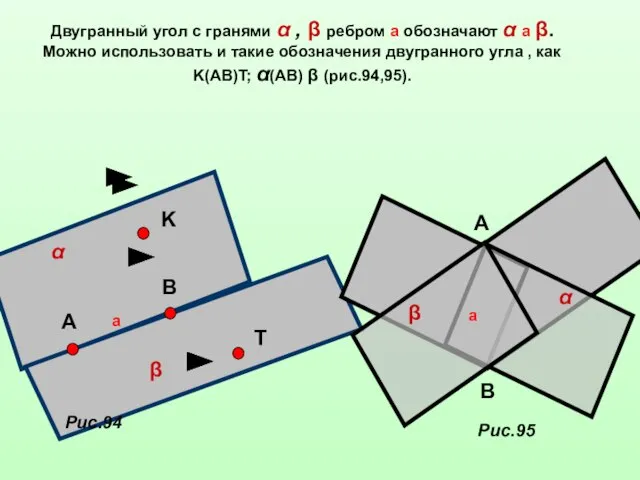
- 4. Двугранный угол с гранями α , β ребром а обозначают α а β. Можно использовать и
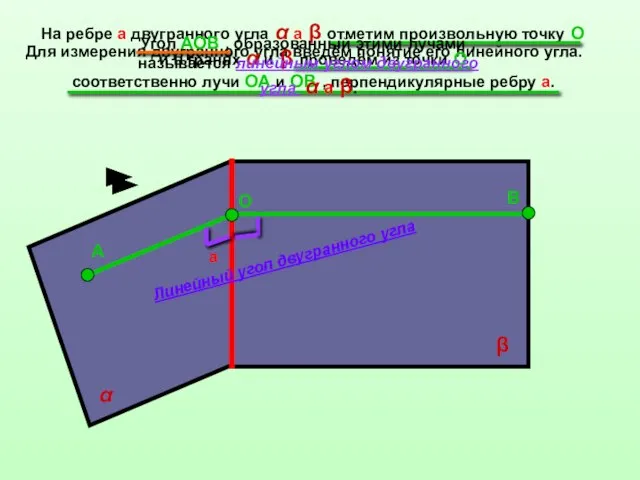
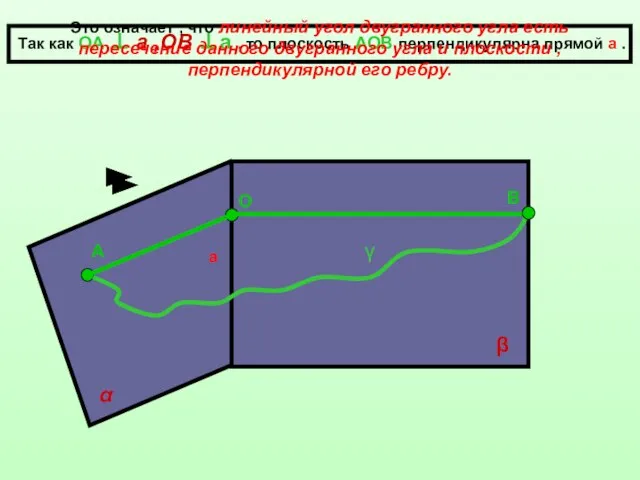
- 5. Для измерения двугранного угла введём понятие его линейного угла. На ребре а двугранного угла α а
- 6. а α β О А В Так как ОА ⊥ а ,ОВ ⊥а , то плоскость
- 7. Теорема : Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. Определение
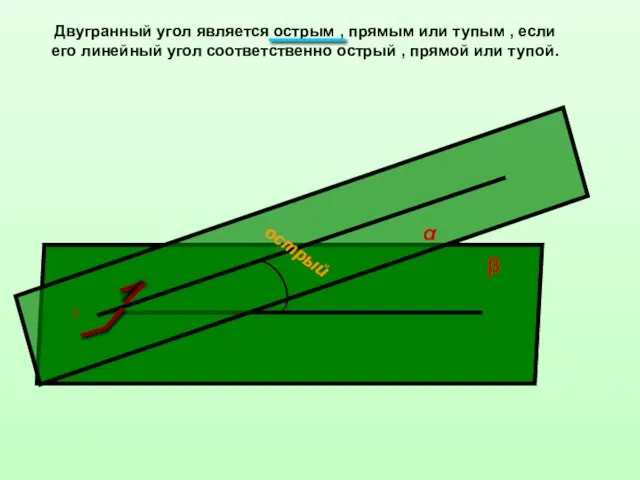
- 8. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
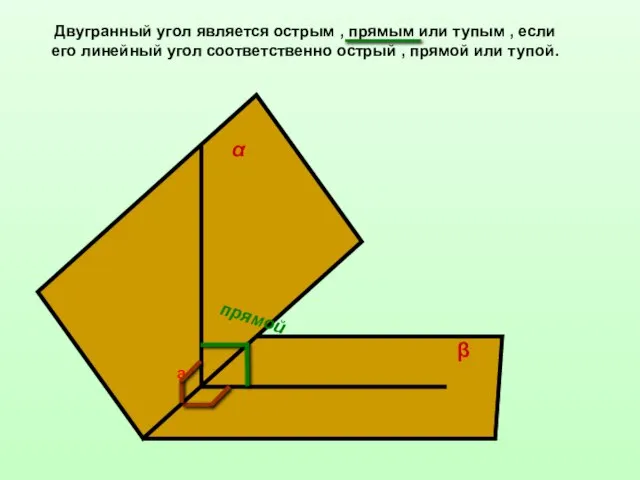
- 9. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
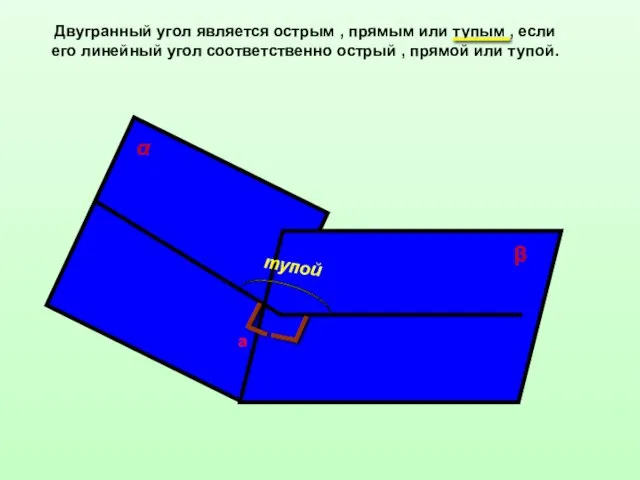
- 10. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
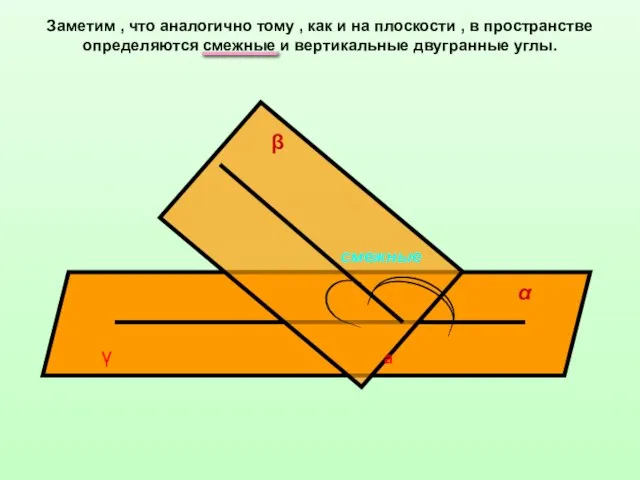
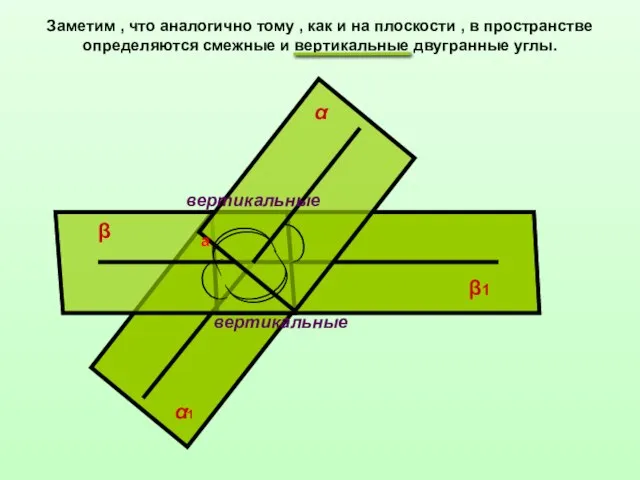
- 11. Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и
- 12. Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и
- 13. Определение : Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов , образованных при их
- 14. β β1 а α α1 с ϕ Величина угла между плоскостями принадлежит промежутку [0°;90°].
- 16. Скачать презентацию


![β β1 а α α1 с ϕ Величина угла между плоскостями принадлежит промежутку [0°;90°].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369938/slide-13.jpg)
 Системы лояльности: современные тенденции развития
Системы лояльности: современные тенденции развития Теорема Виета доказательство
Теорема Виета доказательство Словообразовательные гнёзда полисемантичных имён существительных в русском и белорусском языках
Словообразовательные гнёзда полисемантичных имён существительных в русском и белорусском языках СМАЗКИ КАНАТНЫЕ
СМАЗКИ КАНАТНЫЕ Приемы рисования геометрических фигур
Приемы рисования геометрических фигур Metal-Insulator-Semiconductor and Metal-Insulator-Metal Structures
Metal-Insulator-Semiconductor and Metal-Insulator-Metal Structures "Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов)
"Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов) Три кита в музыке
Три кита в музыке Сбор изображений для тренировки системы распознавания номеров машин
Сбор изображений для тренировки системы распознавания номеров машин Презентация на тему Состав ядра. Ядерные силы (11 класс)
Презентация на тему Состав ядра. Ядерные силы (11 класс) Понятие мотивации. Мотивация по Риссу. Нейрологические уровни Дилтса. Модель ценностей Грейвза
Понятие мотивации. Мотивация по Риссу. Нейрологические уровни Дилтса. Модель ценностей Грейвза Финансовая политика РФ
Финансовая политика РФ Дециметр
Дециметр Материки и океаны
Материки и океаны Конституционное право - ведущая отрасль в правовой системе Российской Федерации. Лекция 1
Конституционное право - ведущая отрасль в правовой системе Российской Федерации. Лекция 1 Александр Родченко
Александр Родченко Спектры.Спектральный анализОткрытый урок
Спектры.Спектральный анализОткрытый урок Лепка фигуры человека
Лепка фигуры человека ОПСиП_ Семенова ПО-3
ОПСиП_ Семенова ПО-3 Градусная сеть на глобусе и географической карте
Градусная сеть на глобусе и географической карте Международный Юридический институт приглашает всех желающих на День Открытых дверей!
Международный Юридический институт приглашает всех желающих на День Открытых дверей! Страхование непредвиденных расходов автовладельцев полис «РЕСОавто ПОМОЩЬ»
Страхование непредвиденных расходов автовладельцев полис «РЕСОавто ПОМОЩЬ» Бюджет доходов и расходов БДР/P&L
Бюджет доходов и расходов БДР/P&L Лексика
Лексика אילו המצאות חדשות הומצאו בישראל ובעולם ?במאה ה?21 -במה תרומתם לאנושות
אילו המצאות חדשות הומצאו בישראל ובעולם ?במאה ה?21 -במה תרומתם לאנושות Главные и второстепенные члены предложения
Главные и второстепенные члены предложения Основные причины ухудшения зрения школьника
Основные причины ухудшения зрения школьника Качество и качества Власти: восприятие населения
Качество и качества Власти: восприятие населения